算法设计与分析.07.网络流 (2)

Posted on Edited on In Views:
最短增流路径，Dinitz 算法，二分图匹配

网络流 (2)

  • Network Flow

Shortest augmenting path

  • FF 中找最短的增流路径
  • BFS 即可

复杂度证明

引理1

  • 最短增流路径的长度是非递减的
  • \(l(v)\)：\(s\to t\) 最短路中边的条数
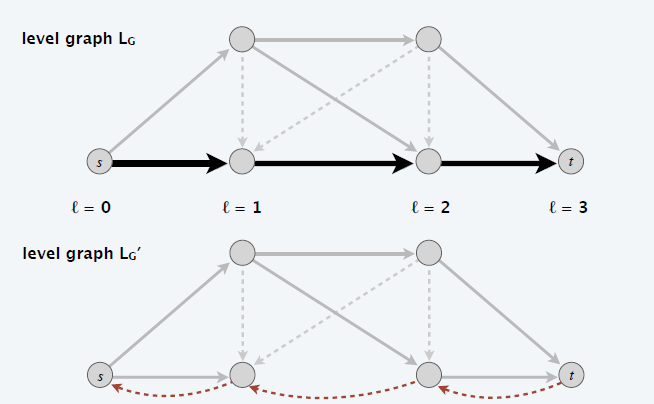
  • level graph：\(L_G=(V,E_G)\)
    • 只包含满足 \(l(w)=l(v)+1\) 的边 \((v,w)\in E\)
  • 那么有
    • P 是图 G 中 \(s\to t\) 的最短路 \(\Leftrightarrow\) P 是图 \(L_G\) 中 \(s\to t\) 的最短路
  • 在增流前后，\(G_f\) 中只会添加反向边，此时新出现的边不会让 level graph 中的边增加
    • 会变少，因为增流了可能删除边
    • 所以最短路不会变短

引理2

  • 每次增流都至少删除一条 bottleneck edge
  • 在 \(s\to t\) 的最短路径变长之前，\(L_G\) 不会发生变化
  • \(s\to t\) 的最短路径变长之后，新构造的 \(L_G\) 中 \(l(v)\) 只增不减
    • 反证法

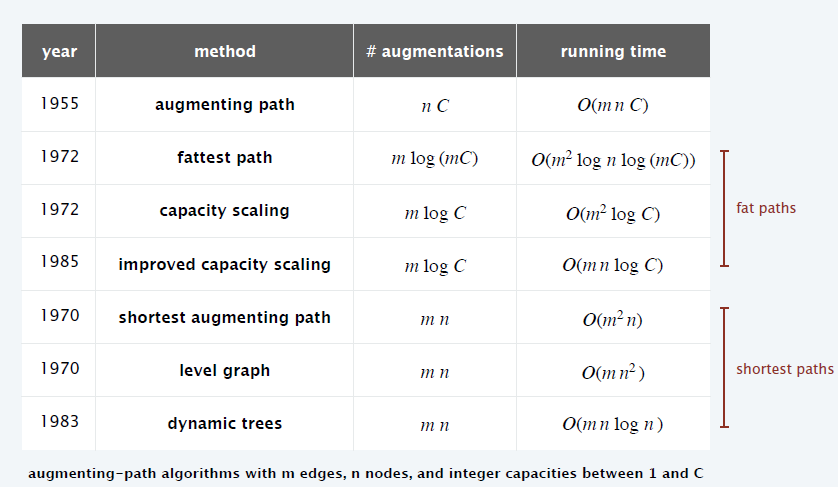
复杂度

  • \(s\to t\) 的最短路不变时，最多有执行 \(m\) 次
  • \(s\to t\) 的最大长度为 \(n-1\)
  • 因此 BFS 最多执行 \(m(n-1)\) 次，BFS 执行时间复杂度 \(O(m)\)
  • 时间复杂度：\(O(m^2n)\)

Dinitz’ algorithm

  • BFS 最短路增流，有两种情况
    • normal：\(s\to t\) 最短路长度不变
    • special：\(s\to t\) 最短路长度变长

normal phase

  • normal：\(L_G\) 只会变小，不会变大
    • 不需要重新构造 \(L_G\)，更新即可

  • get stuck 删除点是为了不重复搜索到这里，浪费时间

伪代码

复杂度

  • per phase：\(O(mn)\)
    • \(L_G\) 初始化：\(O(m)\)
      • BFS
    • 最多增流 \(m\) 次（每次删一条边）：\(O(mn)\)
      • 每次最多更新 \(n-1\) 条边
    • 最多回退 \(n\) 次（每次删除一个点）：\(O(m+n)\)
      • 删边：\(O(m)\)
    • 最多前进 \(mn\) 次：\(O(mn)\)
      • 前进 \(n\) 次便会遇到回退/增流
      • 增流：\(O(mn)\)，重头再来
      • 回退：\(O(n)\)
  • 最多 \(n\) 个 phase
  • 时间复杂度：\(O(mn^2)\)

发展史

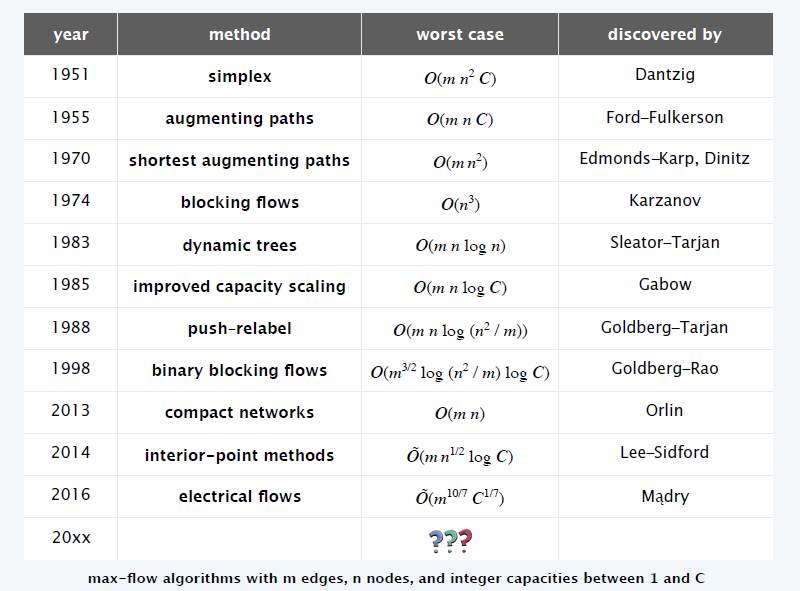
  • 实际应用比较好的算法
    • Push-relabel：\(O(m^{1.5})\)
  • conputer vision
    • Different algorithms work better for some dense problems that arise in applications to computer vision.

simple unit-capacity networks

  • 二分图匹配可以使用最大流算法
    • FF：\(O(mn)\)

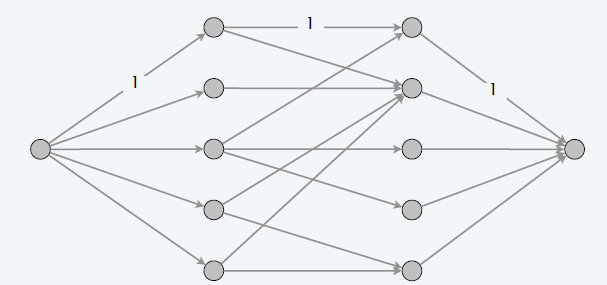
图模型

  • \(c(e)=1,\forall e\in E\)
  • 除了 \(s,t\) 之外，其他要么入度为 1，要么出度为 1
  • 性质
    • \(f\) 是 0-1 flow
    • \(G_f\) 也是 simple unit-capacity networks
  • Dinitz：\(O(mn^{0.5})\)

Dinitz

  • per normal phase：\(O(m)\)
  • phases：\(2\sqrt{n}\)

引理1

  • normal phase 的复杂度：\(O(m)\)
  • 和普通版本区别
    • 找到增流路径之后，删除所有增流路径上的边（都饱和了）
  • 复杂度：\(O(m)\)
    • \(L_G\)：\(O(m)\)
    • 每条边每种情况只会被处理一次：\(O(m)\)
      • 增流、回退、前进
      • ex：不会被增流两次
    • 每个点只会被删除一次：\(O(n)\)
扩展
  • 如果在 simple unit-capacity networks 情况下去掉入度或者出度为 1 的限制
  • normal phase 的复杂度：\(O(m)\)

引理2

  • 经过 \(\sqrt{n}\) 次增流之后，\(val(f)\ge val(f^{\ast})-\sqrt{n}\)
    • \(f^{\ast}\) 是最大流
  • 在 \(\sqrt{n}\) 个 phase 之后，最短增流路径的长度大于 \(\sqrt{n}\)
  • 此时 \(G_f\) 有至少 \(\sqrt{n}\) 层
  • 找到一个层级 \(V_h(1\le h\le\sqrt{n})\)，满足节点数 \(\vert{V_h}\vert\le\sqrt{n}\)
  • 构造割集

\[ A=\{v:l(v)<h\}\cup\{v:l(v)=h\land v\text{ has}\le1\text{ outgoing residual edge}\} \]

  • 注意 \(G_f\) 也是 simple unit-capacity networks
  • 注意此时 \(A\) 的出边分为两个部分，\(h-1\) 层的 \(V_1\)，\(h\) 层的 \(V_2\)
    • \(h\) 层的出边肯定是 1
    • \(h-1\) 层的出边 \((a,b)\) 肯定是指向 \(h\) 层的，
      • \(b\) 有多条出边，因此 \(b\) 只有一条入边，也就是说 \(V_1\) 出来的边数小于 \(V_h\) 中删除的点数
      • 即 \(\vert{V_1}\vert+\vert{V2}\vert\le\vert{V_h}\vert\)

\[ cap_f(A,B)\le\vert{V_h}\vert\le\sqrt{n} \]

复杂度

  • 根据引理2，最多只有 \(2\sqrt{n}\) 个 phase
  • \(O(m\sqrt{n})\)