算法设计与分析.07.网络流 (1)

Posted on Edited on In Views:
网络流算法；最大流和最小割问题，FF 增流算法

网络流

  • Network Flow

max-flow and min-cut problems

  • 最大流、最小割问题

图模型

  • 有向图：\(G(V,E,s,t,c)\)
  • 源 source：\(s\in V\)
    • 假设所有点都是 \(s\) 可达的
  • 汇 sink：\(t\in V\)
  • 容量：\(c(e)\ge0,\forall e\in E\)

最小割

  • s-t cut：\((A,B)\) 是 \(V\) 的一个划分，满足 \(s\in A,t\in B\)
  • 容量（capacity）
    • 只包含 \(A\to B\) 的边，不包含 \(B\to A\) 的边

\[ cap(A,B)=\sum_{e=(a,b),a\in A,b\in B}c(e) \]

  • 最小割：找到一个划分，使得容量最小

最大流

  • s-t flow：满足如下的函数 \(f\)
  • 容量限制（capacity）：\(0\le f(e)\le c(e),\forall e\in E\)
    • 所有边
  • 流守恒（flow reservation）：\(\sum_{e\text{ in to }v}f(e)=\sum_{e\text{ out of }v}f(e),\forall v\in V-\{s,t\}\)
    • 中间节点
  • 流量

\[ val(f)=\sum_{e\text{ out of }s}f(e)-\sum_{e\text{ in to }s}f(e) \]

  • 最大流：找到一个 \(f\)，使得流量最大

Ford–Fulkerson algorithm

贪心算法

  • 不一定能找到最大流
    • 因为每次增流只考虑了 \(s\to t\) 的路径（还可能有反向增流）
    • 一旦一条边上进行增流之后，就不会再进行减流
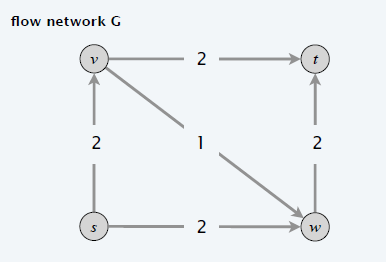
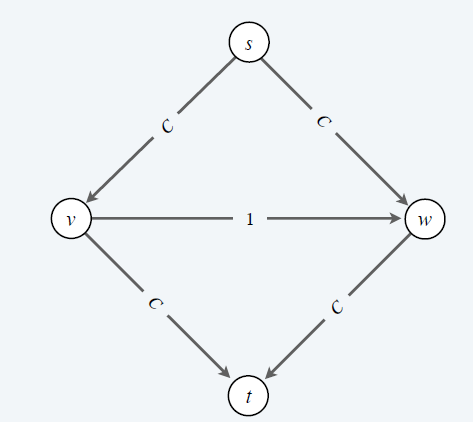
  • 例子
    • 贪心算法如果找到 \(s\to v\to w\to t\)，则不可能找到最大流 \(4\)

残差网络

  • Residual network
  • 原图上加上一条反向边
  • 容量

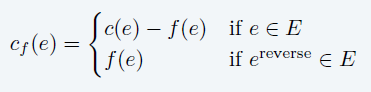
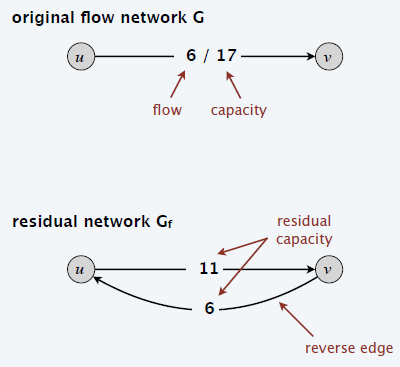
  • 残差网络
    • 边：按照上述定义下，\(c_f(e)>0\) 的边

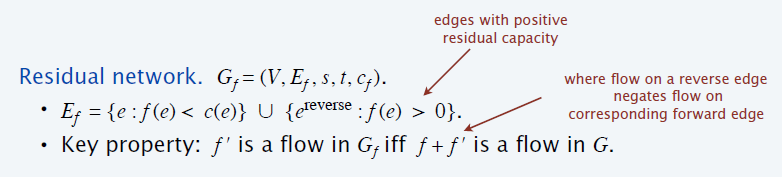
  • \(f'\) 是 \(G_f\) 中的流 \(\Leftrightarrow\) \(f+f'\) 是 \(G\) 中的流
    • 反向边的的流在 \(G\) 的正向边中减去
    • 把 \(G_f\) 上的正向边和反向边合并即证
  • 残差网络的好处：能够减流

增流路径

  • augmenting path
  • \(G_f\) 中的 \(s\to t\) 路径
  • 瓶颈容量（bottleneck capacity）\(\delta\)
    • 增流路径中的最小边权值
    • 用于增流
  • 增流路径 \(P\)

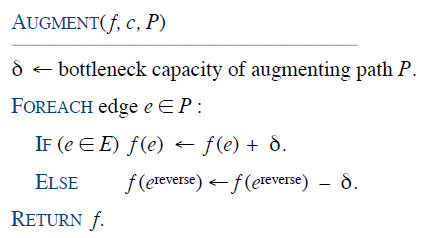
  • 增流之后

\[ val(f')=val(f)+bottleneck(G_f,P) \]

FF 算法

  • 在 \(G_f\) 中不断增流

max-flow min-cut theorem

  • 最大流=最小割

流定理

  • \((A,B)\) 是一个 cut，那么就有如下式子

\[ val(f)=\sum_{e\text{ out of }A}f(e)-\sum_{e\text{ in to }A}f(e) \]

  • 证明：加上 \(A-s\) 所有点的流守恒公式即证

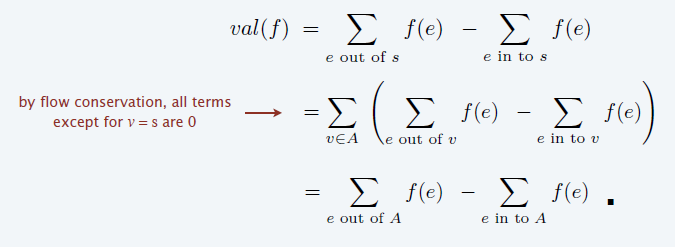
流小于割

  • 对于任意流 \(f\)，任意割 \((A,B)\)，都有 \(val(f)\ge cap(A,B)\)
  • 应用流定理即可

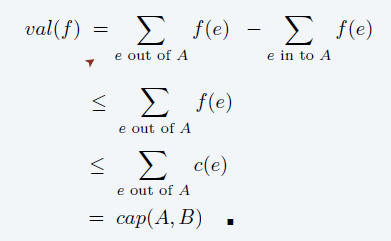
极值

  • 如果存在流 \(f\)，割 \((A,B)\)，满足 \(val(f)=cap(A,B)\)
  • 则 \(val(f)\) 为最大流，\(cap(A,B)\) 为最小割
  • 证明是显然的

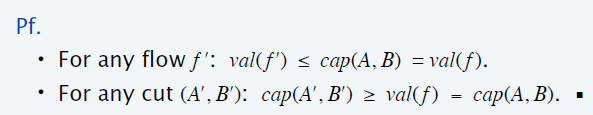
最大流最小割定理

  • 最大流=最小割
    • 能取到等号
  • 增流路径定理
    • \(f\) 是最大流 \(\Leftrightarrow\) 不存在增流路径
  • 等价描述

证明

  • \(\text{i}\to \text{ii}\)：上面的极值定理
  • \(\text{ii}\to \text{iii}\)：反证法
  • \(\text{iii}\to \text{i}\)：构造
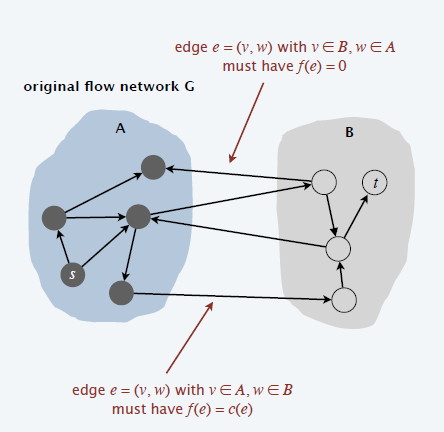
    • 按照 \(G_f\) 中 \(s\) 的可达性，将顶点划分为 \(A,B\)
    • 看原图 \(G\)，此时
      • \(A\to B\) 的边必然是满的 \(f(e)=c(e)\)，否则 \(G_f\) 中存在一条 \(A\to B\) 的边，\(c_f(e)=f(e)-c(e)\)
      • \(B\to A\) 的边必然是空的 \(f(e)=0\)，否则 \(G_f\) 中存在一条 \(A\to B\) 的边，\(c_f(e^{\text{reverse}})=f(e)\)
    • 这种构造满足 \(cap(A,B)=val(f)\)

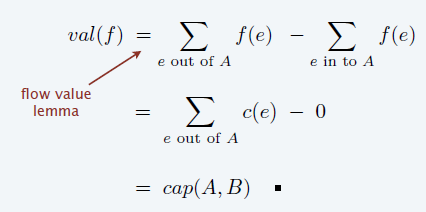
最大流算最小割

  • 时间复杂度：\(O(m)\)
  • 根据上面的构造方法，找到 \(s\) 可达的点，形成 \(A\)，\(B=V-A\)

Capacity-scaling algorithm

FF 分析

  • 假定图 \(G\) 中，\(c(e)\) 都是 \([1,C]\) 之间的整数
  • \(G_f\) 也满足
    • 归纳法，增流路径前后都满足即可
  • FF 算法找增流路径最多执行 \(val(f^{\ast})\le nC\) 次（\(f^{\ast}\) 是最大流）
    • 每次增流至少增加 1
    • \(s\) 出去最多 \(nC\)
  • FF 时间复杂度：\(O(mnC)\)
    • \(O(m)\) 时间找到增流路径
    • BFS/DFS 都可以
  • 存在整数最大流
    • 每一增流的流量都是整数

复杂度

  • 输入规模：\(m,n,\log C\)
  • \(C=\max_e c(e)\)，迭代次数可能也大于 \(C\)
    • 反复横跳，迭代 \(2C\) 次
1
2
3
4
s -> v -> w -> t
s -> w -> v -> t
s -> v -> w -> t
s -> w -> v -> t

扩展

  • 如果 \(c(e)\) 是有理数，FF 可行
    • 乘上分母之积，化为整数
  • \(c'(e)=k\cdot c(e)\)，最小割的划分不变
    • 每一个割集的容量都变为原来的 \(k\) 倍
  • \(c(e)\) 是实数，则不能保证

FF 问题分析

  • 如何找到更好的增流路径

Capacity-scaling algorithm

  • 限定每次增流路径的增流量必须大于 \(\Delta\)

  • 假定：\(c(e)\in [1,C]\)
  • \(\Delta\) 是 2 的整数次幂
    • 易证
  • \(c_f(e),f(e)\) 都是整数
  • 正确性：最后面 \(\Delta=1\)，和原始算法一样了

复杂度

  • scaling phase：\(1+\lfloor{\log_2C}\rfloor\)
  • 算法执行到 \(\Delta\)-scaling phase 结束时，最大流小于等于 \(val(f)+m\Delta\)
    • 同样的划分方式，s 点 \(\Delta\) 可达的点集合 \(A\)

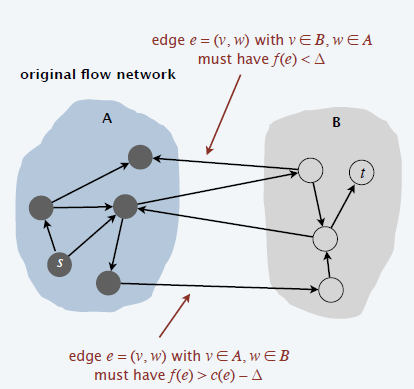
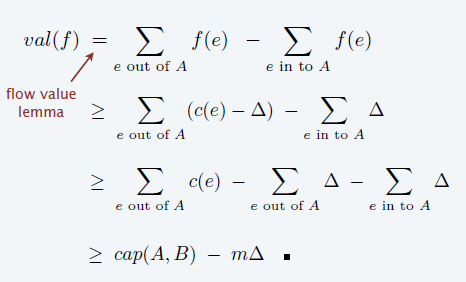
  • 每个 scaling phase，最多增流 \(2m\) 次
    • \(m\Delta\div\dfrac{\Delta}{2}=2m\)
  • 找增流路径：\(O(m)\)
  • 时间复杂度：\(O(m^2\log C)\)