算法设计与分析.06.动态规划 (2)
动态规划 (2)
- DP:Dynamic Programming
sequence alignment
- Edit Distance
- Gap penalty \(\delta\)(空配)
- mismatch penalty \(\alpha_{pq}\)(误配)
- 编辑距离 = 空配 + 误配
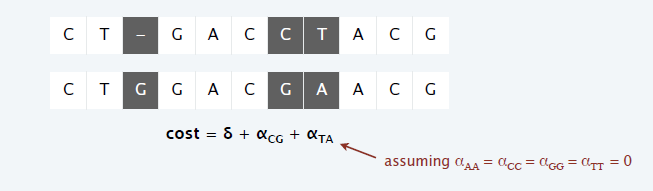
- 给定两个字符串 \(x_1\cdots x_m\) 和 \(y_1\cdots y_n\) ,求最小编辑距离
DP
- \(OPT(i, j)\) :子问题,\(x_1\cdots x_i\) 和 \(y_1\cdots y_j\) 的最小代价
- 原始问题:\(OPT(m,n)\)
- 转移方程
- 最后面两个字符匹配还是不匹配
- \(i=0\lor j=0\Rightarrow OPT(i,j)=(i+j)\delta\)
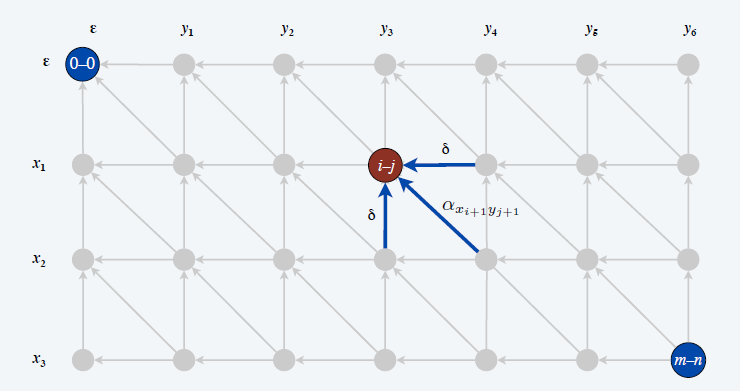
\[ \begin{aligned} OPT(i,j)=\min\{&\\ &OPT(i-1,j-1)+\alpha_{x_iy_j},\\ &OPT(i-1,j)+\delta,\\ &OPT(i,j-1)+\delta,\\ \}&\\ \end{aligned} \]
- 恢复:traceback,判断进入的是哪一个分支(和谁相等)
- 时间复杂度:\(O(nm)\)
- 空间复杂度:\(O(nm)\)
定理
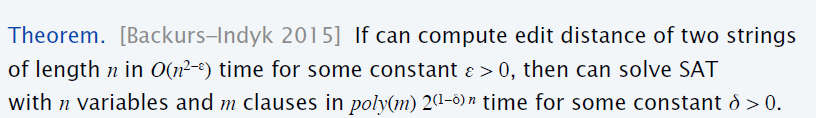
改进
- 空间复杂度:\(O(m+n)\)
- 状态转移只依赖于前一行的值,只需要记录前一行和当前行的值
- \(O(m+n)\)
- 此时无法恢复最优解
- 如何在空间复杂度:\(O(m+n)\)
恢复最优解?
- Hirschberg′s algorithm
Hirschberg′s algorithm
- 能够恢复最优解
- 时间复杂度:\(O(nm)\)
- 空间复杂度:\(O(n+m)\)
- 分治+动归
Edit distance graph
- \(f(i,j)\):\((0,0)\) 到 \((i,j)\) 的最短路
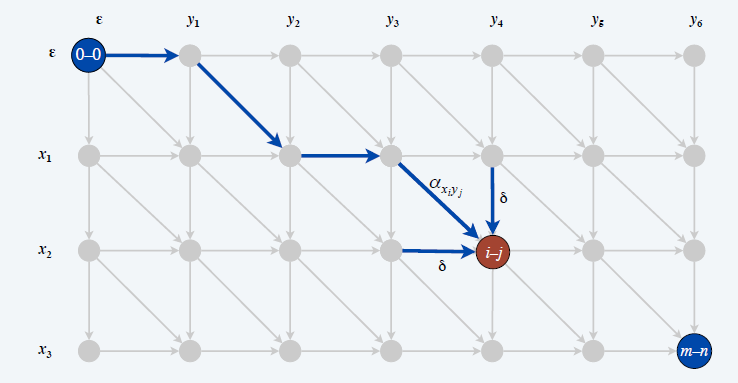
- \(f(i,j)=OPT(i,j)\)
- 归纳法可证
- 对于给定的一列,可以 \(O(mn)\) 时间复杂度,\(O(m+n)\) 空间复杂度计算出 \((0,0)\) 到这一列任意点的最短距离 \(f(i,j)\)
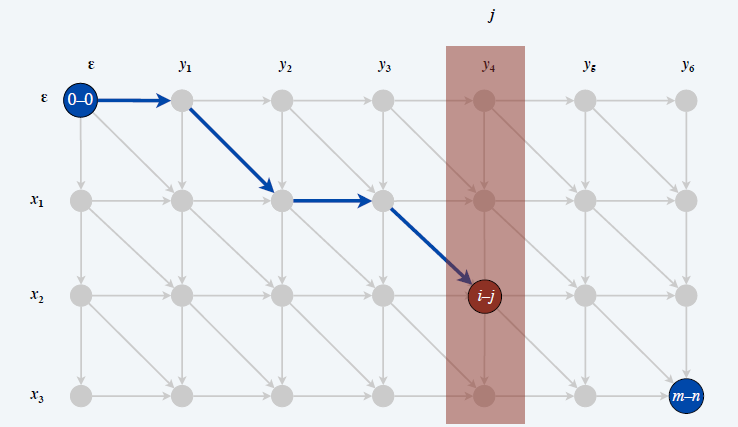
- \(g(i,j)\):\((i,j)\) 到 \((m,n)\) 的最短路
- 将边反向,此时 \((m,n)\) 等价于上面的 \((0,0)\)
- 计算 \(g(i,j)\) 此时等价于上面的 \(f(i,j)\)
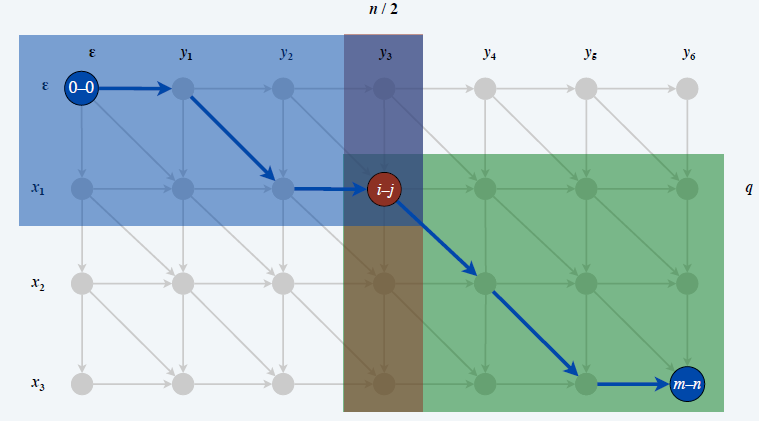
发现
- \((0,0)\) 到 \((m,n)\) 的最短路就是 \(f(i,j)+g(i,j)\)
- 如果 \(q\) 是使得 \(f(q,\dfrac{n}{2})+g(q,\dfrac{n}{2})\) 最小的值,则存在一条\((0,0)\) 到 \((m,n)\) 的最短路经过 \((q,\dfrac{n}{2})\)
- 分治思想
复杂度
- 空间复杂度:\(O(m+n)\)
- 计算 \(f,g\):\(O(m)\)
- 递归时候记录结果,递归次数小于 \(n\):\(O(n)\)
- 时间复杂度
- \(T(m,n)=O(mn\log n)\)
- \(T\) 对于 \(m,n\) 而言都是非降的
简单分析
\[ T(m,n)\le 2T(m,\dfrac{n}{2})+O(mn) \]
- 根据递推
\[ T(m,n)=O(mn\log n) \]
- 分析不紧致,划分的两个子问题实际上更小
- \(T(q,\dfrac{n}{2}),T(m-q,\dfrac{n}{2})\)
严格分析
- \(T(m,n)=O(mn)\)
- 对 \(m+n\) 进行归纳
- 选择一个常数 \(c\),使其满足
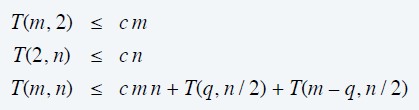
- 对 \(m+n\) 进行归纳 \(T(m,n)\le 2cmn\)
- 代入即可
longest common subsequence
- 最长公共序列
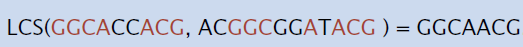
DP1
- 看最后一个字符是否匹配上
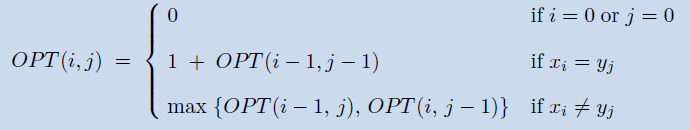
DP2
- 规约为对齐问题
- Gap penalty \(\delta=1\)(空配)
- mismatch penalty \(\alpha_{pq}=\infty\)(误配)
- 结果:\(\dfrac{m+n-\text{edit distance}}{2}\)
理论下界
- No \(O(n^{2−\epsilon})\) algorithm
unless SETH is false
- Tight Hardness Results for LCS and other Sequence Similarity Measures
Bellman–Ford–Moore algorithm
- 最短路问题
- 有向图 \(G(V,E)\),找到从点 \(s\) 到 \(t\) 的最短路
Dijkstra
- 单源最短路
- 不能解决负权边的问题
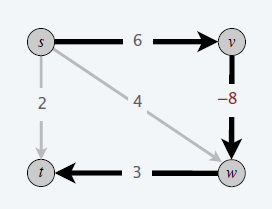
- 调整边权让结果可能出错
- 每条边都加上相同的权重,消除负边
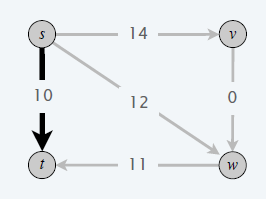
负环
- 负环:环的权重和为负数
- 有负环,则不存在最短路
- 疯狂绕圈圈
- 如果不存在负环,那么最短路一定是简单路径(无环)
- 反证法
- Single-destination shortest-paths problem
- 没有负环的有向图,给定点 \(t\),计算所有其他点到 \(t\) 的最短路
- Negative-cycle problem
- 判定是否存在负环
最短路
- \(OPT(i, v)\):\(v\to t\) 的最多使用 \(i\) 条边的最短路
- 原始问题:\(OPT(n-1,v)\)
- 简单路径最多 \(n-1\) 条边
- 转移方程
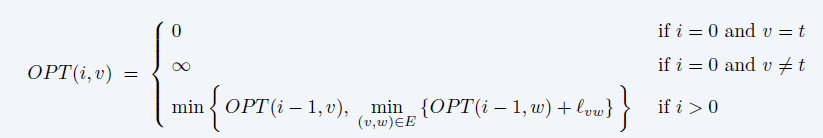
- 算法
- 使用当前点的后继节点开更新当前点
- 记录出边

- 时间复杂度:\(O(nm)\)
- 空间复杂度:\(O(n^2)\)
- 记录矩阵 \(M\)
- 恢复路径
- 每次更新 \(M\) 的时候记录前驱
- \(O(n)\) 空间复杂度
- traceback,看看进入了哪一个分支
- \(O(m)\) 时间复杂度
- 每次更新 \(M\) 的时候记录前驱
优化
- \(d[v]\):目前为止找到的 \(v\to t\) 的最短路的长度
- \(\text{successor}[v]\):目前为止找到的 \(v\to t\) 的最短路的下一个顶点
- 算法
- 使用当前点的前驱节点开更新前驱节点
- 记录入边
- (这样能够实现第1个优化)

- 优化细节
- optm1:如果上一轮迭代中,所有的 \(d[\cdot]\) 都没有更新,则算法结束
- optm2:如果上一轮迭代中 \(d[w]\) 没有更新,则不需要用它去更新其他点
正确性(长度)
- \(d[v]\) 一直都代表这某条 \(v\to t\) 的路径的长度
- 迭代过程中,\(d[v]\) 是非降的
- 第 \(i\) 轮迭代结束后,\(d[v]\) 比使用 \(j(j\le i)\) 条边的路径要短
- 对 \(i\) 做归纳法
复杂度
- 前提是不存在负环
- 时间复杂度:\(O(nm)\)
- 空间复杂度:\(O(n)\)
问题
Q1
- 在中间的某一轮迭代结束后,\(d[w]+e(v,w)\) 可能比 \(d[v]\) 小
- \(w=\text{successor}[v]\)
- 在 \(w\) 更新 \(v\) 之后,可能有其他点更新了 \(w\),此时 \(v\) 并没有跟着更新
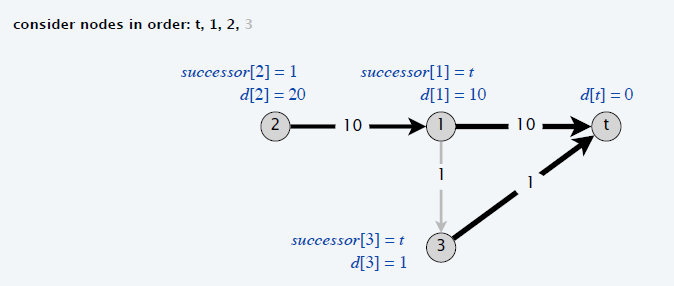
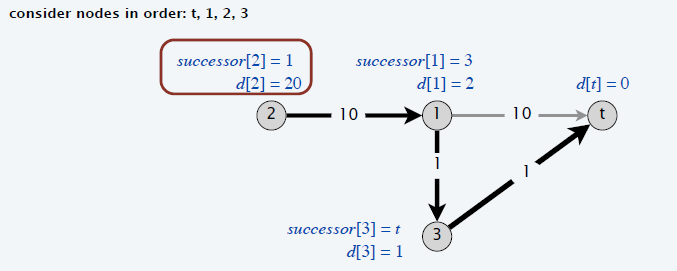
Q2
- 如果存在负环,则后继图可能存在环(互相更新)
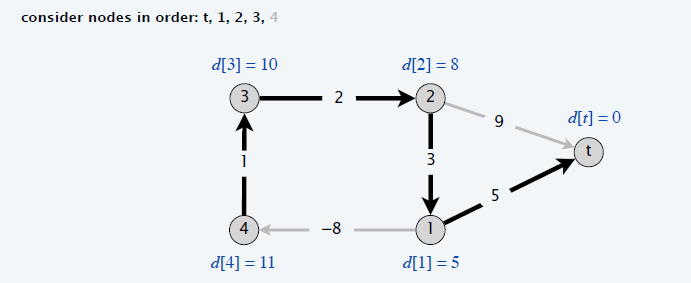
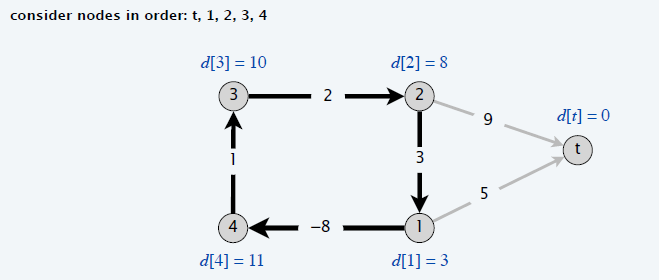
正确性(路径)
- 如果没有负权环,则能够 BF 算法能够找到结果,而且能恢复原始路径
引理
- 后继图中如果有环,则一定是负权环
- 对环上所有边,求和如下不等式
- 当用 \(w\) 更新 \(v\) 时,左右相等
- 但是之后 \(w\) 可能被其他点更新,此时右边更小
\[ w=\text{successor}[v]\Rightarrow d[v]\ge d[w]+l_{vw} \]
证明
- 根据上面引理,后继途中没有环,此时必然存在路径 \(v\to t\)
- 因为算法结束,此时 \(d\) 都没有再更新过了,因此不等式全都取到等号
\[ w=\text{successor}[v]\Rightarrow d[v]= d[w]+l_{vw} \]
- 此时,对路径上的所边求和,可以得到

- 左边是最短路径长度,右边是恢复出来的路径
- 右边和左边相等,因此是最短路
带负权的单源最短路
distance-vector protocols
- 通信网络
- 节点:路由器
- 边:线缆
- 边的长度:延时
- BFM 算法的应用
算法
- Dijkstra’s algorithm:需要网络的全局信息
- Bellman–Ford–Moore:只需要局部信息
- 哪条边先更新无所谓,异步更新也能收敛
- 算法
- 每个路由器保持它到其他节点的最短路,和每一个最短路的下一跳节点
- 每个路由器执行多次计算,每次计算得到到一个终点的最短路
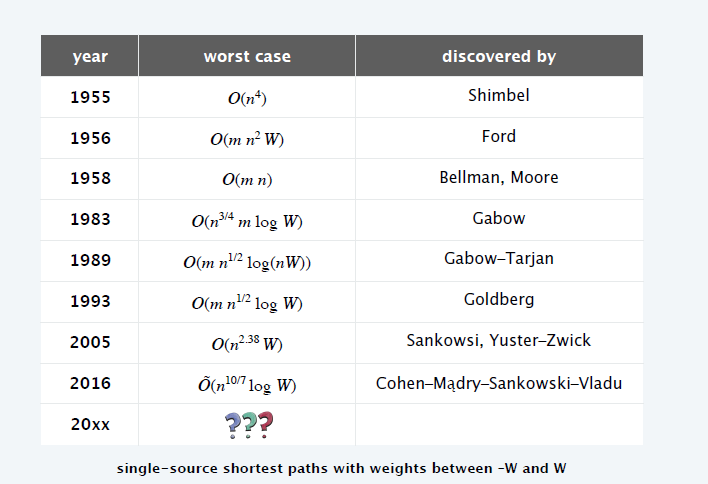
问题
- 边被断开,此时陷入无限循环
算法2
- Path-vector routing protocols

- 基于 Dijkstra 算法,保存整个网络拓扑结构
negative cycles
- 负权环
- 负权环:货币交换,换了一圈,赚了
- BFM 算法能够检测负权环
- 如果满足如下式子,则没有负权环
\[ OPT(n,v)=OPT(n-1,v),\forall v \]
- 如果对于某些节点 v,\(OPT(n,v)<OPT(n-1,v)\),则路径上存在负权环
- \(n\) 条边 \(\Rightarrow\) 有环 \(\Rightarrow\) 删除环之后的路径权值变大(因为现在和更新了) \(\Rightarrow\) 环是负权环
算法
- 时间复杂度:\(O(nm)\)
- 空间复杂度:\(O(n^2)\)
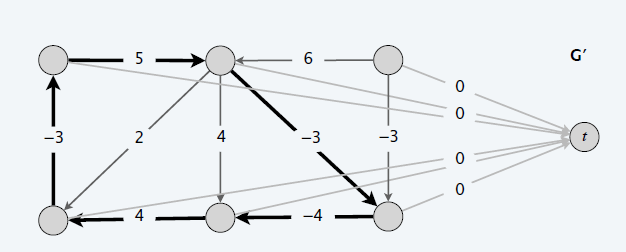
- 算法:加一个顶点和 0 权重的边,跑 BFM 算法 \(n\) 次,看是否收敛
- 检查是否满足 \(OPT(n,v) = OPT(n–1,v)\)
优化
- 时间复杂度:\(O(nm)\)
- 空间复杂度:\(O(n)\)
- BFM 的优化,看第 \(n\) 次迭代有无更新
- 负环,则沿着后继图一直找,找到环就是负环