算法设计与分析.06.动态规划 (1)
动态规划
- DP:Dynamic Programming
DP
- 贪心:短视的做出有利的决定
- 分治:划分为独立的子问题,解决后进行归并
- 动规:分解为可交叉的子问题,汇总子问题的方案
典型算法
- Avidan–Shamir for seam carving.
- Unix diff for comparing two files.
- Viterbi for hidden Markov models.
- De Boor for evaluating spline curves.
- Bellman–Ford–Moore for shortest path.
- Knuth–Plass for word wrapping text in \(\TeX\).
- Cocke–Kasami–Younger for parsing context-free grammars.
- Needleman–Wunsch/Smith–Waterman for sequence alignment.
weighted interval scheduling
- 任务 \(j\),开始时间 \(s_j\),结束时间 \(f_j\),权重 \(w_j>0\)
- 求最大权重和的相容的任务集合
思考
- 贪心:先按照(开始时间,结束时间)排序
- 权重为 1 是正确的
- 权重不为 1 是不正确的
DP
- 按照(结束时间)排序
- \(p(j)\):满足和任务 \(j\) 相容的最大的 \(i\)
- \(OPT(j)\):前 \(j\) 个任务的子问题
- 原始问题,求 \(OPT(n)\)
- 转移方程
- 选不选任务 \(j\)
\[ OPT(j)=\max\{OPT(j-1),OPT(p(j))+w_j\} \]
- \(p(j)+1,\cdots,j-1\) 都和任务 \(j\) 不相容
复杂度
- 排序:\(n\log n\)
- 计算 \(p(j)\),二分:\(n\log n\)
- DP:\(O(n)\)
- 每一个子问题只需要计算一次
实现
Top-Down
- 如果递归的方式实现,需要使用记忆化搜索(有很多相同的子问题)

恢复
- 下面这个算法本质上是在寻找,DP 的时候进入的是哪一个分支

Bottom-Up

maximun subarray problem
- 给定一个数组,数组元素有正有负,找到连续的和最大的子数组
思考
- 枚举
- \(O(n^3)\)
1 | int ans = 0; |
- 预处理,\(sum[i]\) 表示 \(a[0],a[1],\cdots,a[i]\) 的和
- \(O(n^2)\)
1 | int accu = 0; |
DP
- \(O(n)\)
- \(OPT(j)\):前 \(j\) 个元素中,以元素 \(a[j]\) 结尾的最大连续和
- 下标从 1 开始
- 原始问题:\(\max_i OPT(i)\)
- 转移方程
- 只选 \(a_i\),或者加上前面连续的最大值
- \(OPT(1)=x_1\)
\[ OPT(j)=\max\{x_i,x_i+OPT(p(j))\} \]
maximum rectangle problem
- 矩阵中找出和最大的一个矩形区域

- 算法
- 枚举 \(i,j\),表示 \([i,j]\) 列,对这些列的行求和得到数组 \(x\)
- \(O(n)\)
- 对数组 \(x\) 应用上面的
maximun subarray problem算法- \(O(n)\)
- \(n^2\cdot O(n)=O(n^3)\)
- 枚举 \(i,j\),表示 \([i,j]\) 列,对这些列的行求和得到数组 \(x\)
- 计算 \(x\)
- 预计算矩阵 \(S[i,j]\)
- \(S[i,j]=\sum_{k=1}^{j}A[i.j]\)
- 选中 \(i,j\),那么 \(x[k]=S[k,j]-S[k,i-1]-S[k-1,j]+S[k-1,j-1]\)
segmented least squares
Least squares
- 平面上给定 \(n\) 个点,找到一条直线
\(y=ax+b\),使得如下误差最小
- the sum of the squared error
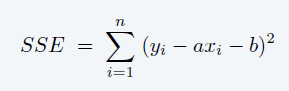
- 有数值解
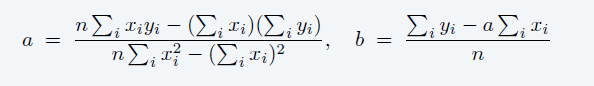
问题
- 分段 SSE,分段函数,每一段都是直线,找最小的 SSE
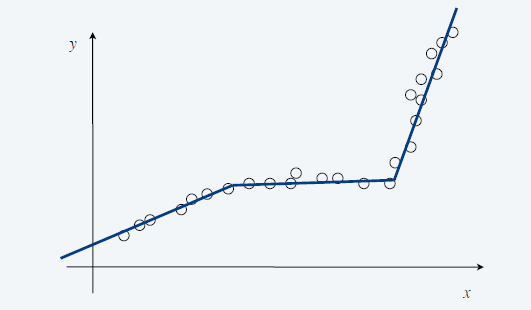
- 最小化 \(f(x)=E+cL\)
- \(E\):每一段的误差
- \(L\):线段
- \(c>0\):权重
DP
- \(OPT(j)\):子问题 \(1,2,\cdots,j\)
- \(e_{i,j}\):\(p_i,\cdots,p_j\) 的 SSE
- 转移方程
- 枚举最后一段折线的长度,然后转化为子问题
- \(OPT(0)=0\)
\[ OPT(j)=\min_{1\le i\le j}\{e_{i,j}+c+OPT(i-1)\} \]
- 计算 SSE
- 预计算 4 个数组 a,b,c,d
- \(\sum_{i}x_i,\sum_{i}y_i,\sum_{i}x_iy_i,\sum_{i}x_i^2\)
- 每一个数组记录 \(\sum_{i=1}^{k}\)
- 此时计算 SSE 为 \(O(1)\) 的
- 例子
- 预计算 4 个数组 a,b,c,d
\[ a[k]=\sum_{i=1}^{k}x_i \]
- 时间复杂度:\(O(n^2)\)
knapsack problem
- 背包问题
- 背包限重 \(W\)
- 每一个物品有一个重量 \(w_i\) 和价值 \(v_i\)
- 让装入背包的物品价值和最高
- 假定权重为整数
DP
- \(OPT(i,w)\):只装前 \(i\) 个物品,限重为 \(w\) 的最大价值
- 原始问题:\(OPT(n,W)\)
- 转移方程
- 装不装当前物品
\[ OPT(i,w)=\max\{OPT(i-1,w),OPT(i-1,w-w_i)+v_i\} \]
\[ i<0\lor w<0\Rightarrow OPT(i,w)=-\infty \]

- 恢复,类似于上面的算法,判断进入哪一个分支
- \(M[i,w]>M[i-1,w]\),则选中了当前物体
- 时间复杂度:\(O(nW)\)
- 伪多项式时间
- 物品编码数量:\(n\)
- 重量 \(w\) 的编码:\(\log W\)
- 空间复杂度:\(O(nW)\)
coin changing
- n 种硬币 \(\{d_1,\cdots,d_n\}\),数量无限,使用最少的硬币实现和为
\(V\)
- 贪心算法只对某些硬币种类有效
DP
- \(OPT(v)\):实现和为 \(v\) 的最小硬币数
- 原始问题:\(OPT(V)\)
- 转移方程
- 枚举不同种类的硬币
- \(OPT(0)=0\)
- \(v\le 0\Rightarrow OPT(v)=\infty\)
\[ OPT(v)=\min_{1\le i\le n}\{1+OPT(v-d_i)\} \]
- 时间复杂度:\(O(nV)\)
RNA secondary structure
- 配对规则
- A-U
- C-G
RNA 二级结构
- 满足配对原则
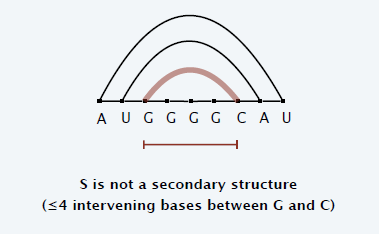
- No Sharp turns
- 配对中间至少存在 4 个间隔
- 下图不行,只隔了 3 个碱基
- No Crossing
- 配对不能交叉
- 下图不行,交叉了
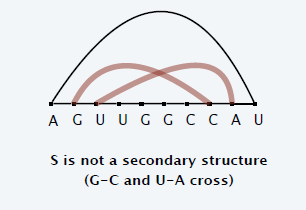
- 最小能量:配对的数量越多,能量越低
DP
- \(OPT(i,j)\):\(b_i\cdots b_j\) 的最大配对数
- 原始问题:\(OPT(1,n)\)
- 转移方程
- \(i\ge j-4\Rightarrow OPT(i,j)=0\)
- \(b_j\) 是否配对
- \(b_j\) 和 \(b_t\) 满足配对原则
\[ \begin{aligned} OPT(i,j)=\max\{&\\ &OPT(i,j-1),\\ &1+\max_{i\le t<j-4}\{OPT(i,t-1)+OPT(t+1,j-1)\}\\ \}&\\ \end{aligned} \]
- 实现:按照区间长度从短到长进行循环

- 时间复杂度:\(O(n^3)\)
- 空间复杂度:\(O(n^2)\)
DP 总结
- Techniques.
- Binary choice:weighted interval scheduling
- 选不选
- Multiway choice:segmented least squares
- 选哪个
- Adding a new variable:knapsack problem
- 增加一个维度
- Intervals:RNA secondary structure
- 区间长度
- Binary choice:weighted interval scheduling