算法设计与分析.05.分治算法 (3)

Posted on Edited on In Views:
傅里叶变换 FFT

分治 (3)

convolution and FFT

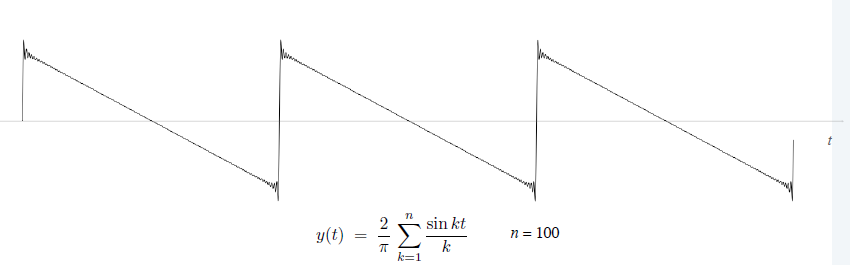
  • 傅里叶定理
    • Any (sufficiently smooth) periodic function can be expressed as the sum of a series of sinusoids.

  • 欧拉定理
    • 好处：Sum of sine and cosines = sum of complex exponentials

\[ e^{ix}=\cos x+i\sin x \]

  • 变换的作用
    • 时域上复杂的信息，频域上可能很简单
  • FFT：Fast Fourier transform
    • 时域频域之间的快速变换
    • Fast way to multiply and evaluate polynomials

参数表示

  • Univariate polynomial（一元多项式）

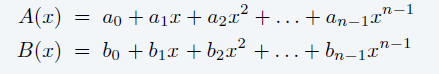
  • Addition：\(O(n)\)
  • Evaluation（求值）
    • Horner’s method

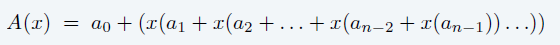
  • Multiplication (linear convolution)
    • Brute Force：\(O(n^2)\)

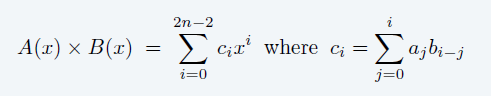
点表示

  • point-value representation
  • 一元 n 次多项式有 n 个复数根
  • n-1 次多项式被 n 个不同的点唯一决定
    • 因此一个 n-1 次多项式能够使用 n 个点表示

操作

  • 加法：\(O(n)\)
    • 点对点加法（\(n\) 个点）
  • 乘法：\(O(n)\)
    • 点对点乘法（\(2n\) 个点）
    • 如何得到这些点的值？

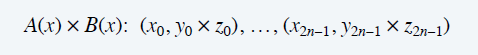
  • 求值：拉格朗日乘子法

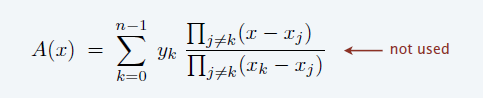
  • trade off

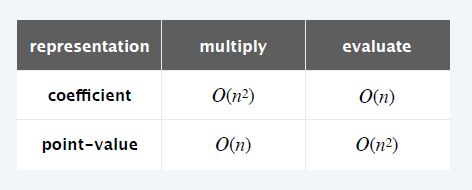
  • 是否有表示方式，乘法和求值都比较快？

Brute Force

参数表示转化为点表示

  • Brute-Force：\(O(n^2)\)
  • 两种方式
    • 矩阵乘向量
    • Horner’s method

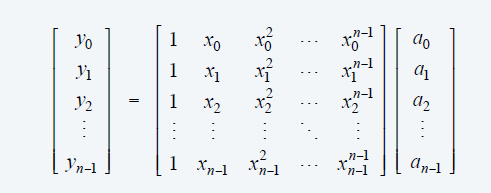
点表示转化为参数表示

  • Brute-Force：\(O(n^3)\)
    • 高斯消去法求解 \(\mathrm{a}\)

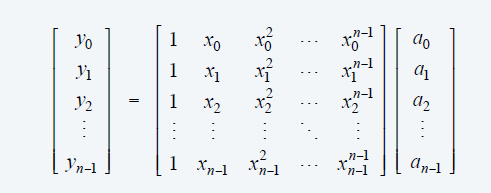
分治

  • 如何多项式求值？
  • 两种方式

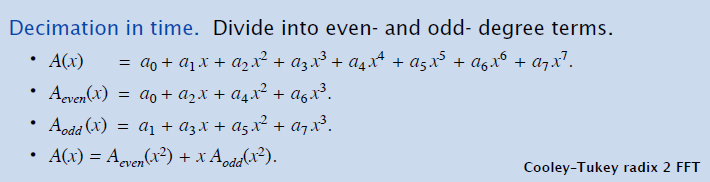
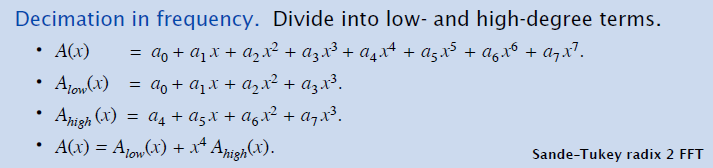
参数表示转化为点表示

  • 奇偶拆分

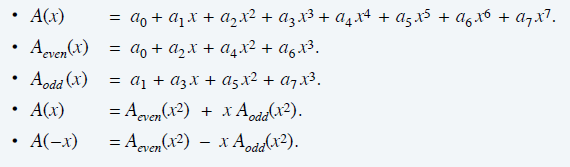
  • 选择 \(x=i,-i,1,-1\)，那么可以通过两个子问题计算，就算出 \(A(x)\)

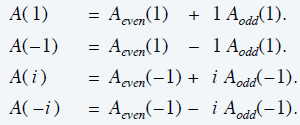
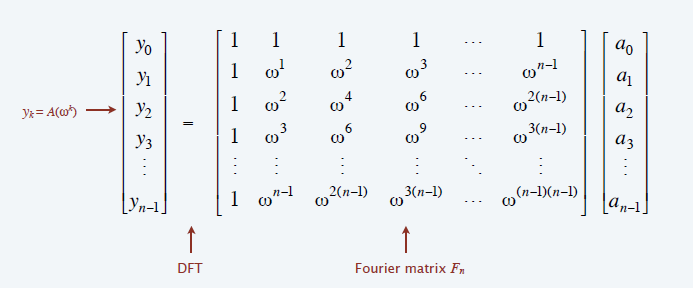
  • 选择 \(x_k=\omega^{k}\) 为 1 的 n 次单位根
    • \(x^n=1\)
    • \(\omega=e^{2\pi i/n}\)

  • n/2 次单位根：\(v=e^{4\pi i/n}=\omega^2\)

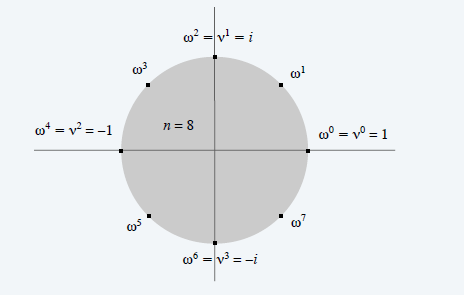
算法
  • \(n\) 表示 \(n\) 次单位根

  • 使用奇偶拆分

\[ 0\le k<n/2 \]

\[ \begin{aligned} y_k &=A(\omega^{k})\\ &=A_{\text{even}}(w^{2k})+w^{k}A_{\text{odd}}(\omega^{2k})\\ &=A_{\text{even}}(v^{k})+w^{k}A_{\text{odd}}(v^{k})\\ \end{aligned} \]

\[ \begin{aligned} y_{k+n/2} &=A(\omega^{k+n/2})\\ &=A(-\omega^{k})\\ &=A_{\text{even}}(w^{2k})-w^{k}A_{\text{odd}}(\omega^{2k})\\ &=A_{\text{even}}(v^{k})-w^{k}A_{\text{odd}}(v^{k})\\ \end{aligned} \]

复杂度

\[ T(n)=2T(\dfrac{n}{2})+\Theta(n)\Rightarrow T(n)=\Theta(n\log n) \]

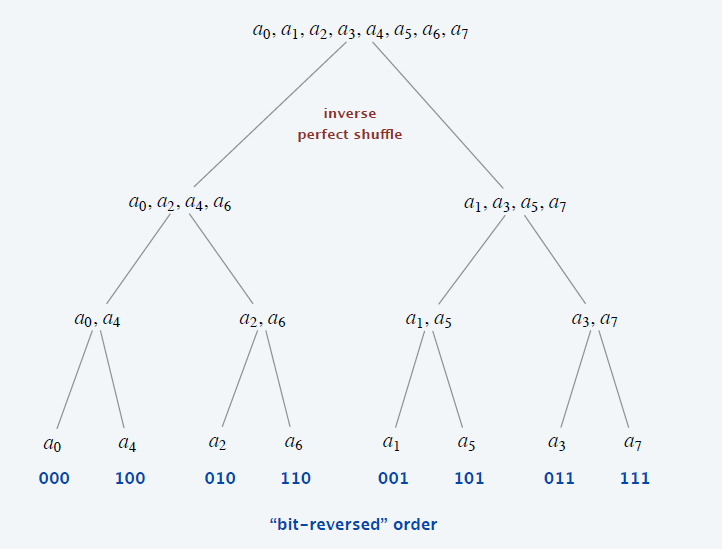
过程
  • 发现最后的顺序是按照比特位的逆序
1
2
3
4
5
6
7
8
000 -> 000
001 -> 100
010 -> 010
011 -> 110
100 -> 001
101 -> 101
110 -> 011
111 -> 111

矩阵形式

点表示转化为参数表示

  • 矩阵求逆

  • 能够显式求逆

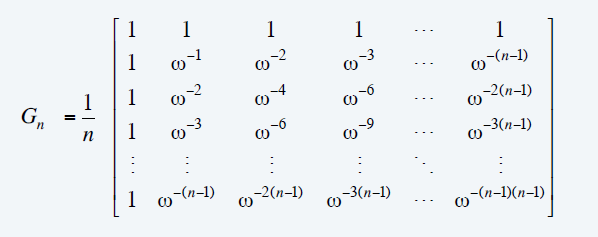
  • 证明是逆矩阵

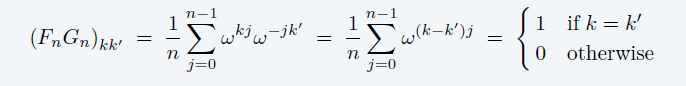
算法
  • 注意最终的结果需要除以 \(n\)

FFT 总结

  • 第一步两次 FFT 形成 2n 个点
    • 把多项式的高位系数看成 0
  • iFFT 的结果，\(c_{2n-1}=0\)

FFT 应用

  • 一个较好的实现
  • Fastest Fourier transform in the West
  • 特点
    • Core algorithm is an in-place, nonrecursive version of Cooley–Tukey
    • 根据硬件编译形成不同的版本
    • \(O(n\log n)\) even when \(n\) is prime
    • Multidimensional FFTs
    • Parallelism

大整数乘法

  • \(a=a_{n-1}\cdots a_0,\;b=b_{n-1}\cdots b_0\)
  • 构造两个 \(n-1\) 次多项式，使用 FFT 求解
  • 结果令 \(x=2\) 即可
  • \(O(n\log n)\) 次浮点运算
  • 注意这里的计算有很多浮点运算，需要保证精度

3-SUM 问题

  • 是否存在三元组 \(i\in X,j\in Y,k\in Z\)，使得 \(i+j=k\)，\(X,Y,Z\) 是整数集合，各含有 \(n\) 个元素
  • 假定：所有整数都在 \([0,m]\) 范围内
  • 实现 \(O(m\log m+n\log n)\)
算法
  • \(O(m\log m+n)\)

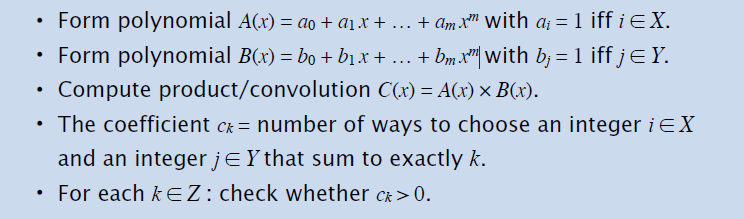
  • \(c_k>0\)：有 \(c_k\) 种选择 \(i,j\) 的方式，实现 \(i+j=k\)