算法设计与分析.05.分治算法 (2)

Posted on Edited on In Views:
主定理，大整数乘法，矩阵乘法

分治 (2)

  • divide and conquer

master theorem

  • 主定理

形式

\[ T(n)=aT(\dfrac{n}{b})+f(n) \]

\[ T(0)=0,T(1)=\Theta(1) \]

  • 参数
    • \(a\ge1\)：子问题个数
    • \(b\ge2\)：子问题规模变小
    • \(f(n)\ge0\)：divide and merge

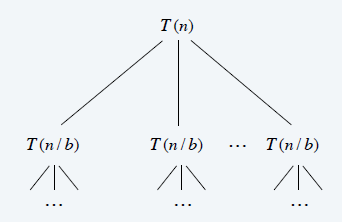
递归树

  • \(a\) = branching factor.
  • \(a^i\) = number of subproblems at level \(i\)
  • \(1 + \log_b n\) levels
  • \(n / b^i\) = size of subproblem at level \(i\)

特例

\[ T(n)=aT(\dfrac{n}{b})+n^c,n=b^k,k\in\mathrm{N} \]

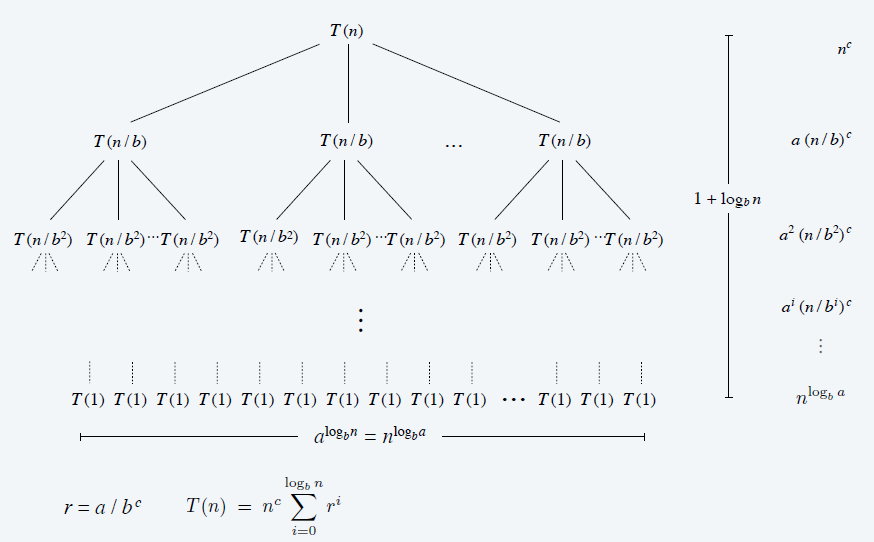
  • 根据递归树

\[ \begin{aligned} T(n) &=a^{\log_b{n}}+\sum_{i=0}^{\log_b{n}-1}a^i(\dfrac{n}{b^i})^c\\ &=n^{\log_b{a}}+n^c\sum_{i=0}^{\log_b{n}-1}r^i\\ &=n^c\sum_{i=0}^{\log_b{n}}r^i\\ \end{aligned} \]

  • \(r=\dfrac{a}{b^c}\) 是一个关键变量

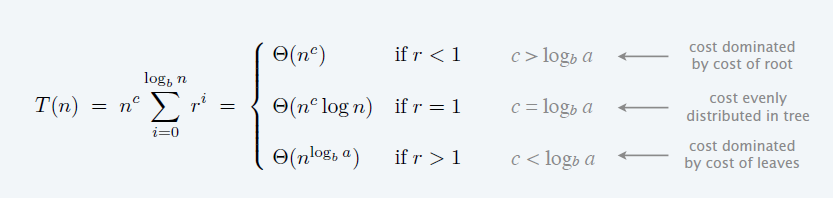
主定理

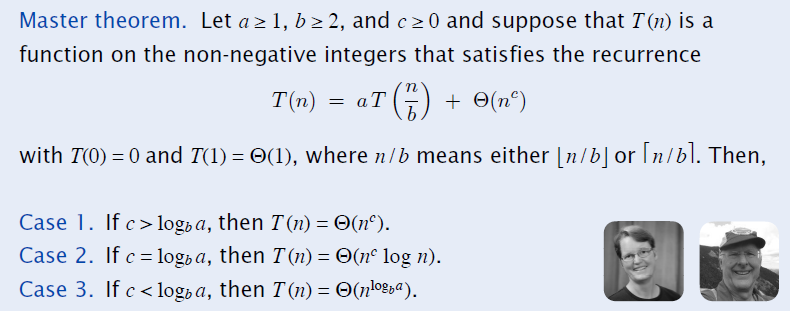
  • 证明思路
    • 先证明 n 是 b 的整数次幂的情况（上面的特例）
    • 扩展到实数域上
    • 处理取整 \(\lceil\rceil,\lfloor\rfloor\)
      • 最多多出来两层

\[ \lceil{n/b}\rceil<{n/b}+1 \]

\[ \begin{aligned} \lceil{\lceil{\lceil{n/b}\rceil/b}\rceil/b}\rceil &<{n/b^2}+(1+1/b+1/b^2)\\ &\le{n/b^2}+2 \end{aligned} \]

  • 扩展
    • \(O\) 取代 \(\Theta\)
    • \(\Omega\) 取代 \(\Theta\)
    • 扩展初始区域：\(T(n)=\Theta(1),n\le n_0\)

局限

  • \(a\) 是 \(n\) 的函数
  • \(a<1\)
  • \(f(n)\) 不满足 \(\Theta(n^c)\) 的形式
    • \(f(n)=n\log n\)

通用定理

integer multiplication

  • 大整数乘法

大整数加法

  • Addition
    • Given two n-bit integers a and b, compute a + b
  • Subtraction
    • Given two n-bit integers a and b, compute a – b.
  • Grade-school algorithm
    • \(\Theta(n)\) 个操作
    • optimal

Grade-school 算法

  • Grade-school algorithm (long multiplication)
  • \(O(n^2)\)

  • optimal？\({\color{red}\mathrm{X}}\)
    • Conjecture（猜想）
      • [Kolmogorov 1956] Grade-school algorithm is optimal
    • Theorem.
      • [Karatsuba 1960] Conjecture is false

分治算法

  • x,y 分别划分为高 n/2 位和低 n/2 位，计算 4 个乘法，然后做加法

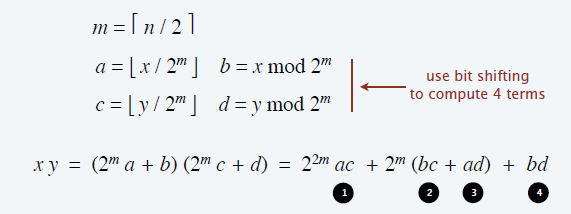\[ T(n)=4T(\lceil\dfrac{n}{2}\rceil)+\Theta(n)\Rightarrow T(n)=\Theta(n^2) \]

Karatsuba multiplication

  • 分治算法的优化

\[ (bc+ad)=ac+bd-(a-b)(c-d) \]

  • 此时乘法计算次数为 3

\[ T(n)=3T(\lceil\dfrac{n}{2}\rceil)+\Theta(n)\Rightarrow T(n)=\Theta(n^{\log_{2}{3}}) \]

整数计算

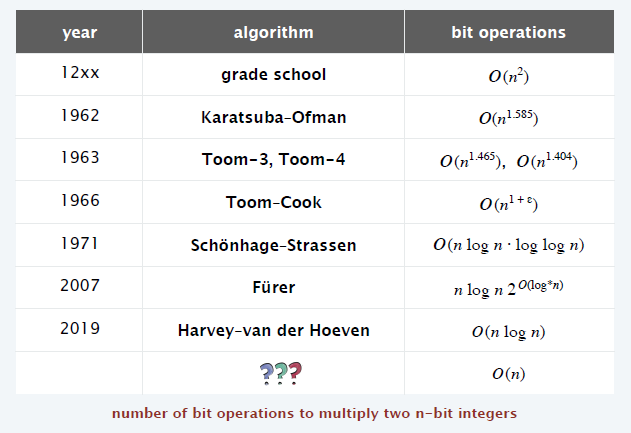
  • \(M(n)\) 表示整数乘法复杂度

  • 发展历程

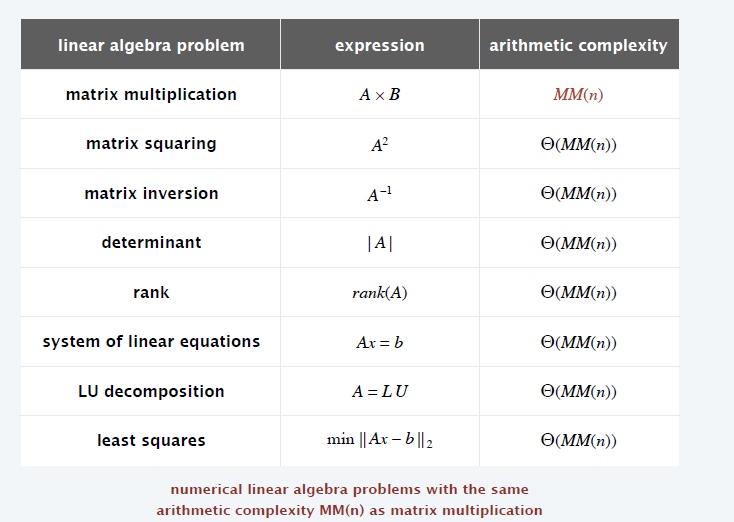
matrix multiplication

  • 矩阵乘法

向量乘法

  • \(a,b\in\mathrm{R}^n\)
  • Grade-school：\(O(n)\)
    • asymptotically optimal

矩阵乘法

  • \(A,B\in\mathrm{R}^{n\times n}\)
  • Grade-school：\(O(n^3)\)
    • optimal？\({\color{red}\mathrm{X}}\)

分块矩阵乘法

\[ T(n)=8T(\dfrac{n}{2})+\Theta(n^2)\Rightarrow T(n)=\Theta(n^3) \]

  • 并没有改进

Strassen’s trick

  • 神奇！

\[ T(n)=7T(\dfrac{n}{2})+\Theta(n^2)\Rightarrow T(n)=\Theta(n^{\log_{2}{7}}) \]

  • 实际操作：当矩阵大小不是 2 的幂次的时候，补 0

  • 问题
    • Sparsity
    • Caching
    • n not a power of 2
    • Numerical stability（浮点数计算）
    • Non-square matrices
    • Storage for intermediate submatrices
    • Crossover to classical algorithm when n is “small”
    • Parallelism for multi-core and many-core architectures
  • 规模足够大的时候，算法优势体现出来

理论

  • Multiply two 2-by-2 matrices with 7 scalar multiplications?
    • Yes! [Strassen 1969]
    • 子矩阵乘法次数为 7
  • Multiply two 2-by-2 matrices with 6 scalar multiplications?
    • Impossible. [Hopcroft–Kerr, Winograd 1971]