算法设计与分析.05.分治算法 (1)
分治
- divide and conquer
总体思路
- Divide up problem into several subproblems (of the
same kind)
- \(O(n)\)
- Solve (conquer) each subproblem recursively
- Combine solutions to subproblems into overall solution
- \(O(n)\)
- 整体时间复杂度:\(O(n\log n)\)
mergesort
- 归并排序
- 有序的好处
- Identify statistical outliers
- Binary search in a database
- Remove duplicates in a mailing l ist
- 应用
- 常见排序应用
- Convex hull
- Closest pair of points
复杂度证明
- \(O(n\log n)\)
- \(T(n)\):max number of compares to mergesort a list of length n
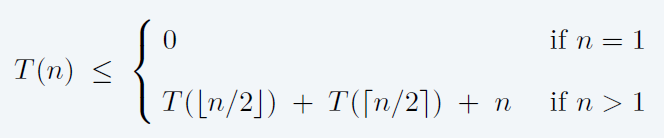
整数次幂
- 假设 \(n\) 为 2 的整数次幂
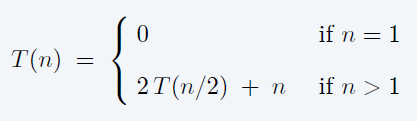
- 证明
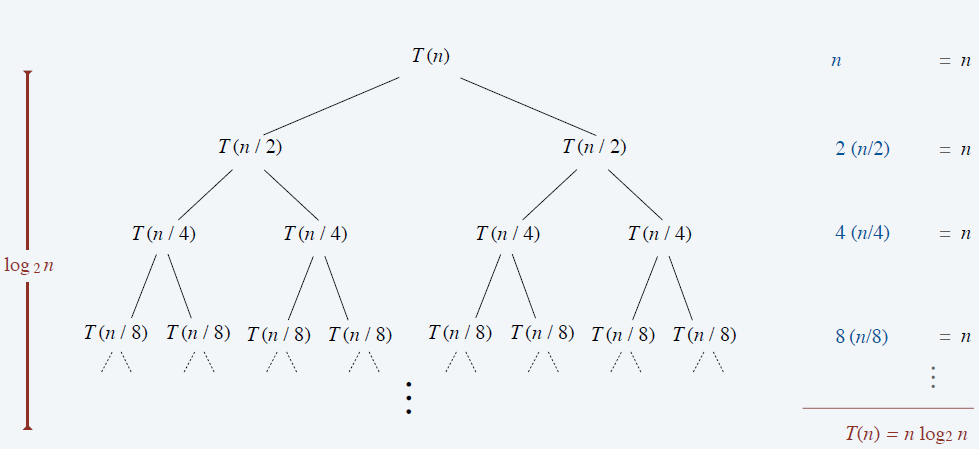
- 归纳法:\(n\to 2n\)
非整数次幂
- \(T(n)\le n\lceil\log_2 n\rceil\)
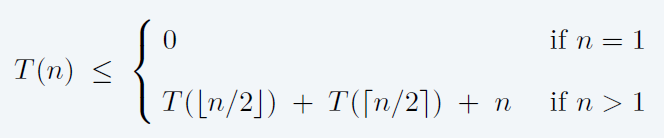
- 归纳法
- Define \(n_1 = \lfloor n/2\rfloor\) and \(n_2 = \lceil n/2\rceil\) and note that \(n = n_1 + n_2\)
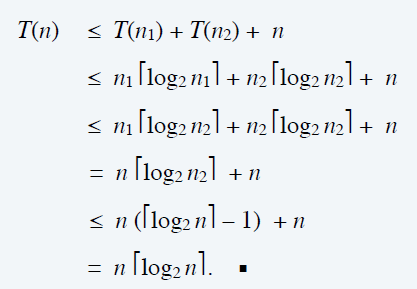
- 最后一个不等号
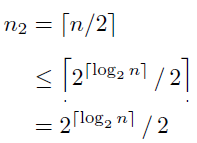
排序的下界
- Comparison trees
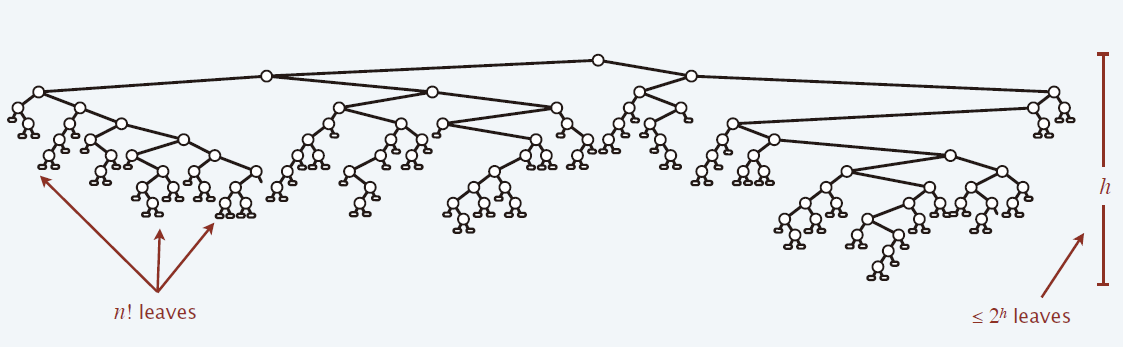
- 假设元素两两不同
- 每一个中间节点表示依次两个元素的对比
- 每一个叶子节点表示一个排序结果
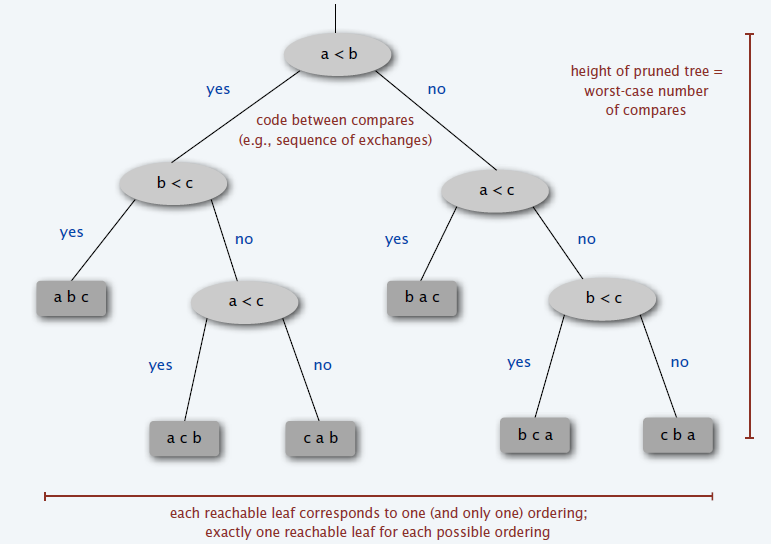
- \(n!\) different orderings \(\Rightarrow\) \(n!\) reachable leaves
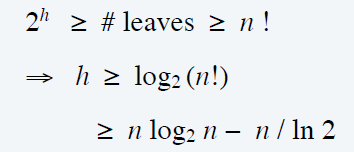
- Note:Lower bound can be extended to include randomized algorithms
例子
- 给定一个 linked list,随机排列它
- 所有排列的可能性相同
- 归并排序的算法步骤,合并的时候随机合并两个数组
- \(O(n\log n)\) time
- \(O(\log n)\) extra space
counting inversions
- 逆序数
- Brute force:\(\Theta(n^2)\)
- check all pairs
- 归并排序,合并的时候计数
- 时间复杂度
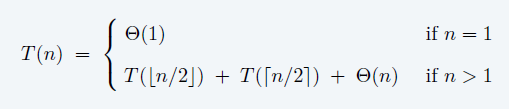
randomized quicksort
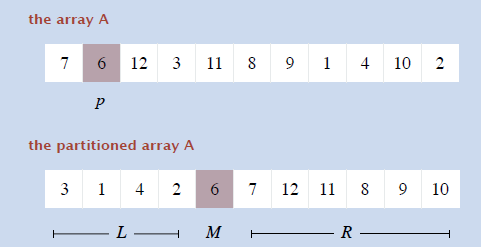
3-way partitioning
- Goal
- 数组 A,元素 p
- 将数组 A 划分为 3 个左中右 3 个部分 L、M、R
- 使得 L 中元素比 p 小,M 中元素和 M 相等,R 中元素比 p 大
- time:\(O(n)\) ,space:\(O(1)\)
算法
- 随机选择一个 A 中的元素 p,应用上面的
3-way partitioning算法划分为 3 个部分,然后递归 L、R 子数组
\[ T(n)=T(i)+T(n-i-1)+\Theta(n) \]
- \(i\) 和选择的 \(p\) 是相关的
复杂度
- 假设排好序之后的数组为 \(a_1<\cdots<a_n\),平均比较次数为 \(O(n\log n)\)
- 利用 BST 树证明
证明
- 构建 BST 树
- 根节点为第一次选择的 pivot element,L 中的元素在左子树之中,R 中的元素在右子树中
- 递归构建
- \(a_i,a_j\) 比较过 \(\Leftrightarrow\) \(a_i,a_j\) 中有一个节点是另外一个结点的祖先节点
- \(a_i,a_j(i<j)\)
比较过的概率如下
- 对于某一次选择 pivot 的时候
- 如果选中了 \(a_i,a_j\),则比较
- 如果选中了 \(a_k(i<k<j)\),则不比较
- 如果选中其他元素,则不影响
- 对于某一次选择 pivot 的时候
\[ \dfrac{2}{j-i+1} \]
- 期望比较次数
\[ \begin{aligned} \sum_{i=1}^{n}\sum_{j=i+1}^{n}\dfrac{2}{j-i+1} &=2\sum_{i=1}^{n}\sum_{j=2}^{n-i+1}\dfrac{1}{j}\\ &\le 2n\sum_{j=2}^{n}\dfrac{1}{j}\\ &\le 2n\sum_{j=1}^{n}\dfrac{1}{j}\\ &\le 2n(\ln n+1) \end{aligned} \]
- 如果存在相同元素,则比较次数只会更少
问题
- 螺丝与螺帽
- 每一个螺丝只能和一个螺帽相配(大小不和)
- n 个螺丝,n 个螺帽
- 每次匹配能够知道螺丝是大了还是小了
- 如何完全匹配上?
- 排序螺孔,二分查找
- \(O(n\log n)+O(n\log n)=O(n\log n)\)
Median and selection problems
- 找出第 k 小的元素(元素之间两两可比)
- \(O(n)\)
randomized quicksort
- 快排的思想,归约为子问题
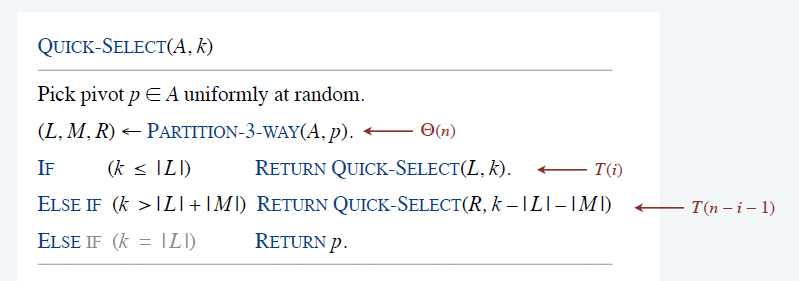
复杂度
- \(T(n,k)\):n 个元素里面找第 k 大
- \(T(n)=\max_{k}T(n,k)\)
- 归纳法能够证明:\(T(n)\le4n\)
- 第一个 \(\le\):我们总选择比较大的一个分支
\[ \begin{aligned} T(n) &\le n+\dfrac{1}{n}\left(2T(\dfrac{n}{2})+\cdots+2T(n-2)+2T(n-1)\right)\\ &\le n+\dfrac{8}{n}\left((\dfrac{n}{2})+\cdots+(n-2)+(n-1)\right)\\ &\le 4n \end{aligned} \]
思考
- 如何在最差的情况下也保证能够实现 \(\Theta(n)\) 的复杂度呢?
\[ T(n)=T(c_1n)+T(c_2n)+\Theta(n) \]
- 满足一个 \(c_1+c_2<1\),则可以推出 \(T(n)=\Theta(n)\)
- 问题:如何找一个划分 \(c_1\),以及一个求解方式 \(c_2\)
MOM selection algorithm
- Median-of-medians selection algorithm
算法
- 找到 pivot
- 将所有元素划分为 \(\lfloor{\dfrac{n}{5}}\rfloor\) 组(5个1组)
- 找到每一组的中位数,在从这些数字里面找到中位数 p
- 把 p 作为 pivot
- 然后运行上面
randomized quicksort接下来的算法
分析
- 小于等于 p 的元素个数至少有这么多个
\[ 3\lfloor{\lfloor{n/5}\rfloor/2}\rfloor=3\lfloor{n/10}\rfloor \]
- 对称的,大于等于 p 的元素也至少有这么多个
- 因此,递归的下一步最多的元素个数如下
\[ n-3\lfloor{n/10}\rfloor \]
- \(C(n)\):数组长度为 n
的最大比较次数
- 5 个元素找中位数的比较次数:6
- 算法
\[ C(n)\le C(\lfloor{n/5}\rfloor)+C(n-3\lfloor{n/10}\rfloor)+6\lfloor{n/5}\rfloor+n \]
- 直观上,规模变小了
\[ \begin{aligned} C(n) &\le C(n/5+n-3n/10)+11n/5\\ &=C(9n/10)+11n/5\\ \end{aligned} \]
\[ C(n)\le22n \]
- 问题:上面的不等式不一定成立
- 不一定单调非降(取整去不掉)
证明
\[ T(n)=\max_k{C(k)},k\le n \]
- \(T(n)\) 是单调非降的
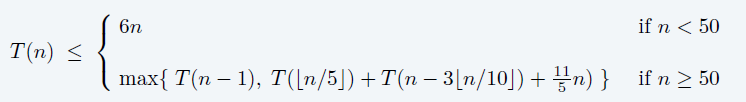
- \(n<50\):mergesort
\[ n\log n\le n\log50\le 6n \]
- 归纳法证明:\(T(n)\le44n\)
思考
- 划分的时候,k(3, 5, 7) 个一组,最差情况下谁更差?
- 3 差于 5 差于 7
BFPRT
- [Blum–Floyd–Pratt–Rivest–Tarjan 1973]
- There exists a compare-based selection algorithm whose worst-case running time is \(O(n)\)
- Optimized version of BFPRT:\(\le5.4305 n\) compares
- Upper bound: [Dor–Zwick 1995] \(\le2.95 n\) compares
- Lower bound: [Dor–Zwick 1999] \(\le(2 + 2^{−80}) n\) compares
- 实用性:常数太大不实用
closest pair of points
- 平面最近点对
- Goal:平面中有很多点,找到欧式距离最近的两个点
- 如果这些点都在一条线上:\(O(n\log
n)\)
- 排序+扫描
- 最近点对排序后一定是相邻的
- 假定:所有的点都不相同
分治
- 算法时间复杂度:\(O(n\log^2 n)\)
- 预处理:按照 x 轴排序
- \(O(n\log n)\)

- 每一个点只需要和接下来的 7 个点做检测
- 每一个框内最多只会有 1 个点(不然距离比 \(\delta\) 小)
- 框外的点距离都大于 \(\delta\)
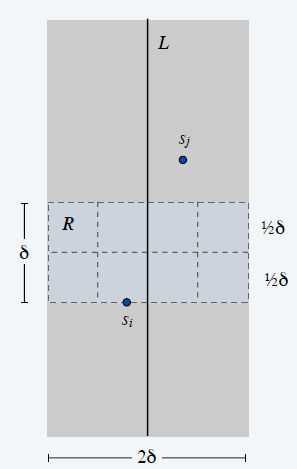
改进
- 时间复杂度:\(O(n\log n)\)
- y 轴的排序可以修改成归并,每一个子问题返回的时候,返回一个 y 轴排好序的列表,则当前问题的按照 y 轴排序就变成一个归并操作(同时剔除到 L 的距离大于 \(\delta\) 的点)
理论
- 基于欧氏距离的平面最近点对,基于比较的方式,下界如下
- [Ben-Or 1983, Yao 1989]
- In quadratic decision tree model, any algorithm for closest pair (even in 1D) requires \(\Omega(n \log n)\) quadratic tests
- uses the floor function
- [Rabin 1976]
- There exists an algorithm to find the closest pair of points in the plane whose expected running time is \(O(n)\)
应用
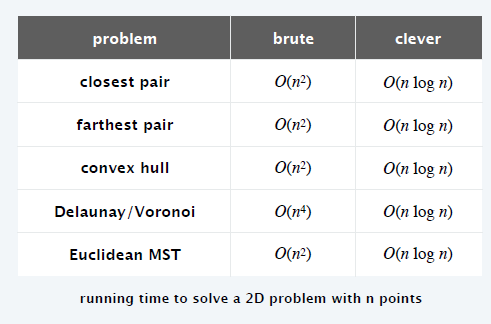
- 高维空间还是个谜
Convex hull
- 凸包
- 找一个最小的凸多边形,把所有点包起来
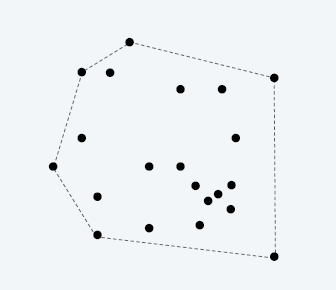
- 从 y
值最小的点出发,找到所有点和这个点连成的直线,找到满足所有点都在左侧的直线,这个点为下一个点
- 斜率排序
- 反复这个过程,直到找到起始点,找到凸包
Farthest pair
- 最远点对
- 最远点对一定在凸包上
- 旋转卡壳法
- 最远点对必然属于对踵点对集合
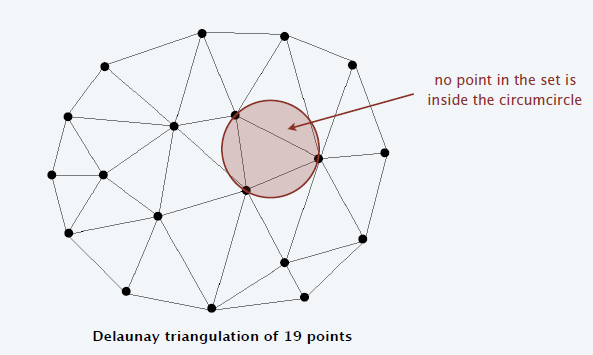
Delaunay triangulation
- 点集的三角剖分,要求每一个三角形的外接圆内部没有其他点
- 要求任意四点不能共圆
- 性质
- No edges cross.
- Among all triangulations, it maximizes the minimum angle.
- 最正
- Contains an edge between each point and its nearest neighbor
Euclidean MST
- 最小生成树,距离度量为点与点之间的欧拉距离
- Euclidean MST is subgraph of Delaunay triangulation.