VAE(Auto Encoding Variational Bayes)

Posted on Edited on In Views:
训练一个隐空间到最终结果的映射，隐空间中的变量影响最终结果

Auto Encoding Variational Bayes

方法

问题描述

  • 数据集 \(\mathrm{X}=\left\{\mathrm{x}^{(i)}\right\}_{i=1}^{N}\) 是 \(N\) 个独立同分布的样本
  • 假设 \(\mathrm{x}^{(i)}\) 是由一个连续的随机变量 \(\mathrm{z}\) 产生的
  • 过程如下
    • 首先根据某个先验分布 \(p_{\theta^\ast}(\mathrm{z})\) 产生一个样本 \(\mathrm{z}^{(i)}\)
    • 然后再根据条件概率 \(p_{\theta^\ast}(\mathrm{x}\vert\mathrm{z})\) 生成样本 \(\mathrm{x}^{(i)}\)
  • 假设 \(p_{\theta^\ast}(\mathrm{z}),p_{\theta^\ast}(\mathrm{x}\vert\mathrm{z})\) 来自于参数族分布 \(p_{\theta}(\mathrm{z}),p_{\theta}(\mathrm{x}\vert\mathrm{z})\)，他们对于 \(\theta,\mathrm{z}\) 都是几乎处处可导的
  • 问题：我们不知道真实的 \(\theta^\ast\) 和隐变量 \(\mathrm{z}\)

适用

  • 不对后验分布做简化的假设，适合通用场景
  • Intractability
    • \(p_{\theta}(\mathrm{x})=\int p_{\theta}(\mathrm{z})p_{\theta}(\mathrm{x}\vert\mathrm{z})\;\mathrm{dz}\) 很难估计和求导（不能直接用最大似然估计）
    • \(p_{\theta}(\mathrm{z}\vert\mathrm{x})=p_{\theta}(\mathrm{x}\vert\mathrm{z})p_{\theta}(\mathrm{z})/p_{\theta}(\mathrm{x})\) 不好求（不能使用 EM 算法）
      • EM（Expectation Maximization）
      • 随机初始化 \(\theta\)
      • E-step：估计 \(p_{\theta}(\mathrm{z}\vert\mathrm{x})\)
      • M-step：更新 \(\theta\)
    • mean-field VB（Variational Bayesian）算法也不能运行
    • 比较常见，当似然函数 \(p_{\theta}(\mathrm{z}\vert\mathrm{x})\) 比较复杂的时候
      • 带非线性激活层的神经网络
  • A large dataset
    • batch optimization is too costly
    • 希望使用更小的 batch，甚至是单个数据点
    • 基于采样的方法开销大，例如 MC-EM，采样很耗时

说明

  • 我们的方法试图解决如下 3 个问题
    • 快速估计 \(\theta\)
    • 快速估计 \(p_{\theta}(\mathrm{z}\vert\mathrm{x})\)
    • 快速估计 \(p_{\theta}(\mathrm{x}\vert\mathrm{z})\)
  • recognition model \(q_{\phi}(\mathrm{z}\vert\mathrm{x})\)
    • 对复杂的后验分布 \(p_{\theta}(\mathrm{z}\vert\mathrm{x})\) 的估计
    • 和变分推断的限制不一样，我们不要求是可因子化的，参数 \(\phi\) 也不需要从闭式期望中求出
  • 我们提出一个方法能够将 recognition model \(q_{\phi}(\mathrm{z}\vert\mathrm{x})\) 和 generative model parameters \(\theta\) 一起训练的学习方法
  • encoder：\(q_{\phi}(\mathrm{z}\vert\mathrm{x})\)
  • decoder：\(p_{\theta}(\mathrm{x}\vert\mathrm{z})\)

The variational bound

  • marginal likelihood，给定 \(\theta\) 下的 \(\mathrm{x}\) 的分布的似然函数

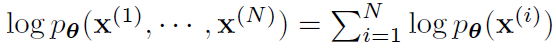
  • 重写每一个项（EQ1）

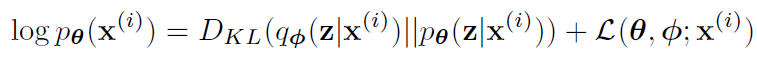
  • KL 散度是非负的，因此 \(\mathcal{L}\) 项也被称为 (variational) lower bound

\[ D_{KL}(p(x)\Vert q(x)) = \int p(x)\log\left(\frac{p(x)}{q(x)}\right) \mathrm{d}x \]

  • 以下的 \(\mathrm{x}\) 代表 \(\mathrm{x}^{(i)}\)
    • Eq2

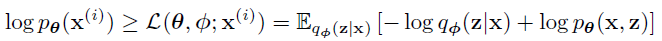
  • 推导

\[ \begin{align} \mathcal{L}(\theta, \phi ;\mathrm{x}^{(i)}) &=\log p_{\theta} (\mathrm{x}^{(i)}) - D_{KL}(q_{\phi} (\mathrm{z}|\mathrm{x}^{(i)}) \Vert p_{\theta} (\mathrm{z}|\mathrm{x}^{(i)}))\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})} [\log p_{\theta} (\mathrm{x})]-\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})} [\log q_{\phi} (\mathrm{z}|\mathrm{x}) - \log p_{\theta} (\mathrm{z}|\mathrm{x})]\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})} \Big[\log \Big(p_{\theta} (\mathrm{x})p_{\theta} (\mathrm{z}|\mathrm{x})\Big)-\log q_{\phi} (\mathrm{z}|\mathrm{x})\Big]\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})} [\log p_{\theta} (\mathrm{z},\mathrm{x})-\log q_{\phi} (\mathrm{z}|\mathrm{x})] \end{align} \]

  • 也可以重写为如下式子
    • Eq3

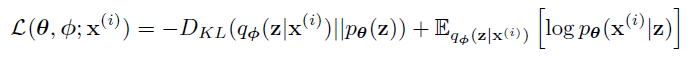
  • 推导

$$ \[\begin{align} \mathcal{L}(\theta, \phi ;\mathrm{x}^{(i)}) &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})}\left[\log p_{\theta} (\mathrm{z},\mathrm{x})-\log q_{\phi} (\mathrm{z}|\mathrm{x})\right]\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})}\left[\log \left(\dfrac{p_{\theta} (\mathrm{z},\mathrm{x})}{q_{\phi} (\mathrm{z}|\mathrm{x})}\right)\right]\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})}\left[\log \left(\dfrac{p_{\theta} (\mathrm{x}\vert\mathrm{z})p_{\theta} (\mathrm{z})}{q_{\phi} (\mathrm{z}|\mathrm{x})}\right)\right]\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})}\left[\log p_{\theta} (\mathrm{x}\vert\mathrm{z})+\log p_{\theta} (\mathrm{z})-\log q_{\phi} (\mathrm{z}|\mathrm{x})\right]\\ &=\mathbb{E}_{q_{\phi} (\mathrm{z}|\mathrm{x})}[\log p_{\theta} (\mathrm{x}\vert\mathrm{z})]-D_{KL}(q_{\phi} (\mathrm{z}|\mathrm{x}) \Vert p_{\theta} (\mathrm{z}))\\ \end{align}\] $$

  • 通过优化 \(\theta,\phi\) 让下界最小化
  • \(\mathcal{L}\) 对 \(\phi\) 求导困难
    • \(\mathrm{z}\) 的具体分布不知道，随意采样会导致方差很大
    • 按照分布采样的估计

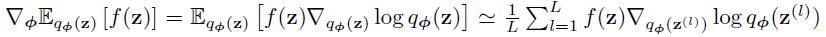
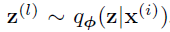
image-20221030111014197

SGVB estimator

  • a practical estimator of the lower bound and its derivatives
  • 假设后验分布的形式为 \(q_{\phi}(\mathrm{z}\vert\mathrm{x})\)
    • 也可以应用在 \(q_{\phi}(\mathrm{z})\)
  • The fully variational Bayesian method for inferring a posterior over the parameters is given in the appendix.
    • 看附录
  • 我们可以重参数化一个随机变量 \(\hat{\mathrm{z}}\sim g_{\phi}(\epsilon,\mathrm{x})\)
    • \(g\) 可微分的
    • 其中 \(\epsilon\) 是一个已知分布的随机噪声
    • 如何选择看后面
  • 现在可以构造一个对 \(f(\mathrm{z})\) 的通用的 MC 估计

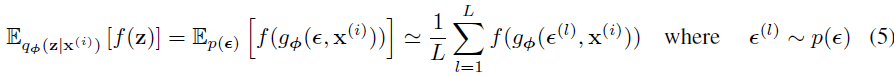
  • 将其应用在Eq2，得到 SGVB（Stochastic Gradient Variational Bayes）估计

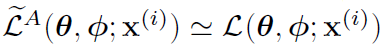
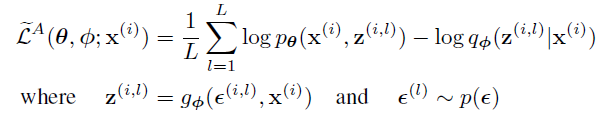
  • 通常 Eq3 中的 KL 散度部分能被显式积分得到（见附录），只有重建误差需要通过采样估计
  • 因此得到一个方差更小的估计

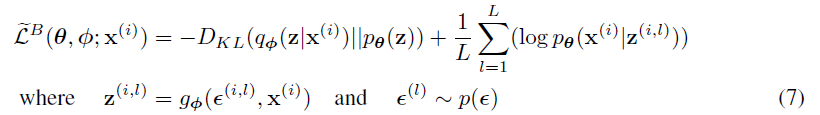
AEVB algorithm

参考资料