算法设计与分析.04.贪心算法 (2)
贪心算法 (2)
- Dijkstra′s algorithm
- minimum spanning trees
- Prim, Kruskal, Boruvka
- single-link clustering
- min-cost arborescences
Dijkstra′s algorithm
- 单源最短路问题
- Single-source shortest paths problem
- 输入为边权不为负的有向图,给定起始节点,求这个节点到所有其他节点的最短路
应用
- PERT/CPM
- Map routing
- Seam carving
- 图像放缩,蛮有趣的
- Seam Carving -- 基于内容的图像缩放算法
- Robot navigation
- Texture mapping
- Typesetting in LaTeX
- Urban traffic planning
- Telemarketer operator scheduling
- Routing of telecommunications messages
- Network routing protocols (OSPF, BGP, RIP)
- Optimal truck routing through given traffic congestion patter
书籍
- Network Flows: Theory, Algorithms, and Applications, by Ahuja, Magnanti, and Orlin, Prentice Hall, 1993.
算法

证明
- 不变量:对于任意集合 \(S\) 中的结点
\(u\),\(d[u]\) 都表示最短路径的长度
- 对 \(\vert{S}\vert\) 进行归纳
优化
- 直接保存 \(\pi(v)\),而不是通过上面的方式计算
- 当某一个点 \(u\) 加入到 \(S\) 中时,才使用 \(u\) 的出边 \(edge(u,v)\) 去更新 \(\pi(v)\)
- 使用最小值优先的优先队列去保存 \(\pi(v)\)
- \(\pi(v)\) 只会越来越小
伪代码实现
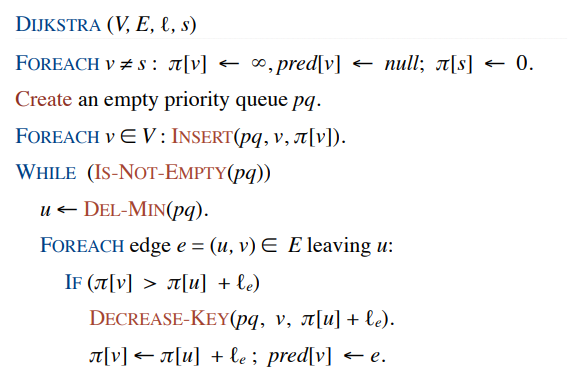
优先队列选择
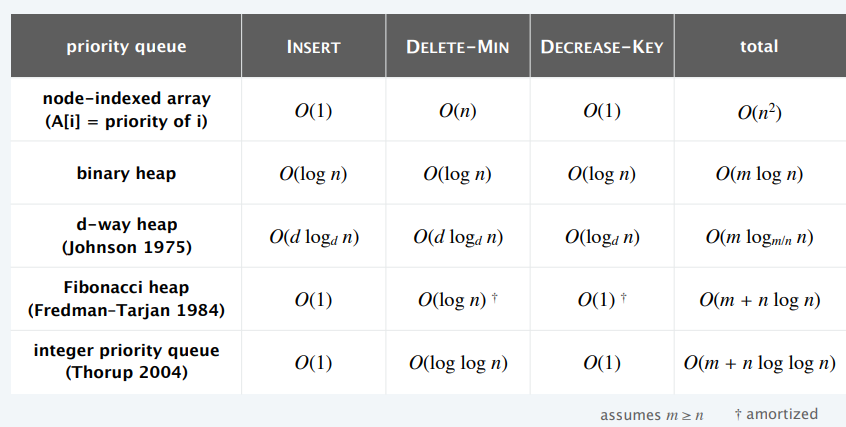
无向图
- [Thorup 1999]
- Can solve single-source shortest paths problem in undirected graphs with positive integer edge lengths in \(O(m)\) time
- Does not explore nodes in increasing order of distance from \(s\)
相关问题
- Shortest paths in undirected graphs: \(\pi[v]\le \pi[u]+l(u, v)\)
- Maximum capacity paths: \(\pi[v]\ge \min\{\pi[u], c(u, v)\}\)
- Maximum reliability paths: \(\pi[v]\ge\pi[u]\times\gamma(u, v)\)
- 迷宫问题:允许打破 \(k\)
道墙的最短路
- BFS,需要记录状态还剩打破几道墙的机会
最小生成树
- minimum spanning trees
定义
环和割集
- Path(路径)
- Cycle(环):首尾结点相同,其余节点两两不同的路径
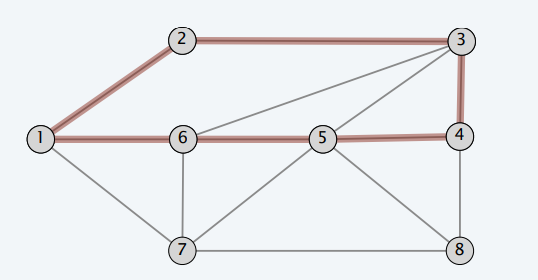
- Cut(割):顶点划分的两个集合
- Cutset(割集):连接顶点划分的两个集合之间的边
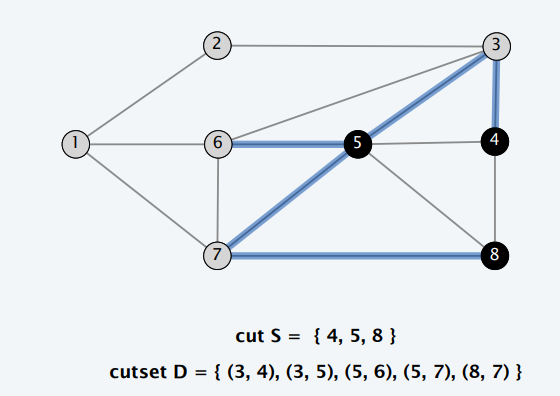
定理
- 任意一个环和割集之间的公共边数量一定为偶数(包括0)
- 画图证明
生成树
- 无向连通图 \(G(V,E)\) 的生成树
\(H(V,T)\)
- 包含所有顶点 + 连通 + 无环
- 如果 \(H\) 是无向连通图 \(G\) 的子图,如下是一些等价说法
- \(H\) is a spanning tree of \(G\)
- \(H\) is acyclic and connected
- \(H\) is connected and has \(\vert{V}\vert – 1\) edges
- \(H\) is acyclic and has \(\vert{V}\vert – 1\) edges
- \(H\) is minimally connected:removal of any edge disconnects it
- \(H\) is maximally acyclic:addition of any edge creates a cycle
最小生成树
- MST:Minimum spanning trees
- 边权之和最小的生成树
- Cayley’s theorem
- The complete graph on n nodes has \(n^{n–2}\) spanning trees
应用
- Dithering.
- Cluster analysis.
- Max bottleneck paths.
- Real-time face verification.
- LDPC codes for error correction.
- Image registration with Renyi entropy.
- Find road networks in satellite and aerial imagery.
- Model locality of particle interactions in turbulent fluid flows.
- Reducing data storage in sequencing amino acids in a protein.
- Autoconfig protocol for Ethernet bridging to avoid cycles in a network.
- Approximation algorithms for NP-hard problems (e.g., TSP, Steiner tree).
- Network design (communication, electrical, hydraulic, computer, road).
基本环
- Fundamental cycle
- 任意一条非树边 \(e\in E\) 都能和树
\(H\) 上的边 \(T\) 组成一个唯一的环 \(C_e\)
- 对于任何一条环 \(C_e\) 上的边 \(f\in C_e\),\((V,T\cup\{e\}-f)\) 还是生成树
- 如果 \(c(e)<c(f)\),则 \(H\) 不是 MST
基本割集
- Fundamental cut
- 任意一条树边 \(e\in T\) 都能将树
\(H\) 划分为两个不连通的子集,形成割集
\(D_e\)
- 对于任何一条割集 \(D_e\) 上的边 \(f\in D_e\),\((V,T\cup\{e\}-f)\) 还是生成树
- 如果 \(c(e)<c(f)\),则 \(H\) 不是 MST
贪心算法
- Red rule(红规则):找到没有红边的环,将权值最大的边染成红色
- Blue rule(蓝规则):找到没有蓝边的割集,将权值最小的边染成蓝色
- 贪心算法
- 反复应用红规则和蓝规则,直到所有边都着色,此时所有的蓝色边形成 MST
- (存在 \(\vert{V}\vert-1\) 条蓝色边是就可以停止)
证明
- 不变量:存在一棵最小生成树,它包含所有的蓝色边,不包含任何的红色边
- 利用基本树变换实施归纳法
- 证明算法终止的时候,蓝色边形成 MST
- 根据上面的不变量,只需要证明最终所有的边都着色了即可
- 如果存在 \(e\) 未着色
- 如果 \(e\) 的两端都属于同一分支 \(\Rightarrow\) 树 + \(e\) 形成环 \(\Rightarrow\) 红规则
- 如果 \(e\) 的两端不属于同一分支 \(\Rightarrow\) \(e\) 形成割集 \(\Rightarrow\) 蓝规则
Prim, Kruskal, Boruvka
- 最小生成树算法
Prim
- Prim:一直使用蓝规则
- 从一个点出发,找割集中最小边
- \(O(m\log n)\)
- 类似于 Dijkstra 算法实现
Kruskal
- Kruskal:贪心算法
- 找最小边
- 如果和已选择的边成环,舍去(红规则)
- 如果未和已选择的边成环,选择它(蓝规则)
- \(O(m\log m)\)
- 判定是否成环使用并查集,\(O(1)\) 判断
Reverse-delete algorithm
- Reverse-delete algorithm:贪心算法
- 所有边降序排列,过一遍所有边,如果不会让图不连通,则删除它
- [Thorup 2000]:\(O(m\log n(\log\log n)^3)\)
Boruvka algorithm
- Boruvka algorithm:一直使用蓝规则
- 对所有的树分支应用蓝规则
- \(O(m\log n)\)
- 每一轮:\(O(m)\)
- 计算所有连通分支
- 过一遍所有边,记录所有连通分支之间的最小边
- 选中最小边
- 最多 \(\log_2 n\) 轮
- 每一轮:\(O(m)\)
实现
- Contraction version(收缩边实现)
- 收缩每一个树分支,删除重边和自环
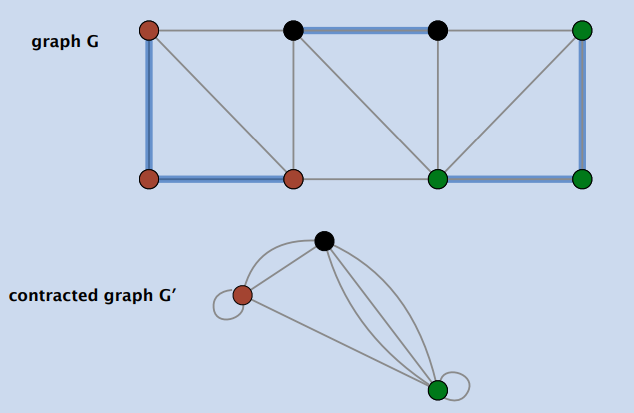
- 收缩边的步骤:\(O(m+n)\),结果:\(G(V,E)\Rightarrow G'(n',E')\)
- 计算 \(n'\) 个连通分支
- 对于每一个点,使用 \(id[u]=i\) 记录结点 \(u\) 属于第 \(i\) 个连通分支
- \(G\) 中的边 \(e(u,v)\) \(\Rightarrow\) \(G'\) 中的边 \((id[u],id[v])\)
- 细节:
- 去除自环:判断下即可(\(id[u]\ne id[v]\))
- 去除重边
- 对所有的边 \(e(i,j)\) 构造 \(i-j(i<j)\)
- 按照字母序排序(基数排序 \(O(n)\) )
- 去除重边即可
平面图
- 如果图 \(G\) 是平面,则算法能在 \(O(n)\) 内实现
- 平面图(planar)
- 能够在平面画成没有相交边的图
- \(\Leftrightarrow\) 没有同构于 \(K_{3,3}\) 或 \(K_5\) 的子图
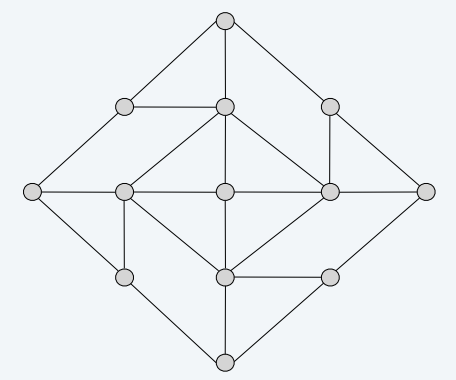
- 平面图收缩点、删除边之后还是平面图
- 对于简单平面图:\(m\le 3n\)
- 算法时间:
\[ O(cn)+O(c\dfrac{n}{2})+O(c\dfrac{n}{4})+\cdots=O(n) \]
A hybrid algorithm
- Boruvka–Prim algorithm
- 先运行 Boruvka \(\log\log n\) 次,然后再运行 Prim
- 贪心算法的特例
- Boruvka:\(O(m\log\log n)\)
- 结果图:\(\vert{V}\vert\le n\log_2 n,\vert{E}\vert\le m\)
- Prim(Fibonacci heaps 实现)
\[ O(m+\dfrac{n}{\log n}\log(\dfrac{n}{\log n}))=O(m+n) \]
进展
- 确定性算法

随机算法
[Fredman–Willard 1990]:\(O(m)\) in word RAM model.
[Dixon–Rauch–Tarjan 1992]:\(O(m)\) MST verification algorithm.
[Karger–Klein–Tarjan 1995]:\(O(m)\) randomized MST algorithm.
最小瓶颈生成树
- Minimum Bottleneck Spanning Tree
- 最大边最小的生成树
- minimizes the most expensive edge
- 结论(无向图)
- MST 一定是 MBST
- MBST 不一定是 MST
single-link clustering
- 把一些点分成 \(k\) 堆,让堆与堆之间的距离最大
应用
- Routing in mobile ad-hoc networks.
- Document categorization for web search.
- Similarity searching in medical image databases
- Cluster celestial objects into stars, quasars, galaxies.
定义
- 距离函数(distance function)

算法
- Kruscal 的算法步骤,剩下 \(k\) 个连通分支就结束
- 先找最小生成树,然后删除最长的 \(k-1\) 条边
分析
- 算法可行(MST 删除最长的 \(k-1\) 条边的结果满足条件)
- 证明如下(反证法)
- MST 删边之后形成的边集为 \(C\),包括连通分支 \(C_1,\cdots,C_k\)
- 假设存在一个边集 \(C^{\ast}\),满足 \(p,q\) 在 \(C\) 中都属于连通分支 \(C_i\),但是在 \(C^{\ast}\) 中属于两个连通分支 \(C^{\ast}_i,C^{\ast}_j\)
- 那么有 \(\text{distance}(C^{\ast}_i,C^{\ast}_j)\le\text{distance}(p,q)=d_{p,q}\)
- 但是根据删边算法规则,\(C\) 中任意两个子集之间的距离都大于等于 \(d_{p,q}\),也就是说 \(\text{distance}(C^{\ast}_i,C^{\ast}_j)\) 小于等于 \(C\) 中任意两个子集之间的距离
- 根据 \(p,q\) 任意性,如果有不同,则距离就更小
- 得证
min-cost arborescences
- arborescence:有根树
- 有向图 \(G(V,E)\) 的根节点为 \(r\) 的有根树 \(T(V,F)\)
- \(T\) 去除方向之后是 \(G\) 的一棵生成树
- 对于任意一点 \(v\in V-\{r\}\) ,都存在从 \(r\) 到这个节点的唯一路径
性质
- \(G(V,E)\) 的子图 \(T(V,F)\) 是根节点为 \(r\) 的有根树
- \(\Leftrightarrow\) 没有有向环,除了 \(r\) 之外,所有节点入度为 \(1\)(\(r\) 入度为 \(0\))
- \(\Rightarrow\):定义即证
- \(\Leftarrow\):沿着入边一定能找到 \(r\)
最小有根树
- Min-cost arborescence problem
- Goal:给定有向图 \(G\),所有边权大于等于 \(0\),指定根节点 \(r\),找到边权和最小的有根树
充分最优条件
- 对于除了 \(r\) 之外的结点,选择权值最小的入边,如果此时选择的边形成了有根树,那么这一定是最小有根树
- 证明显然
\[ \text{cost}(T)=\sum_{j}e_{i,j}\ge\sum_{j}\min_{i,\text{edge}(i,j)\in E}\{e_{i,j}\} \]
- 可能不是有根树
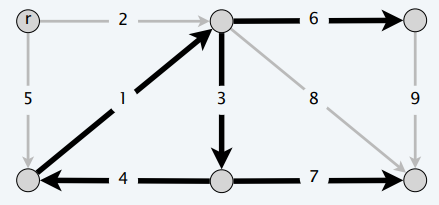
Reduced costs
- 对于所有的边权值做一个变换
- 对于点 \(\forall v\in V-\{r\}\),对他的入边做如下操作:所有的入边的权值减去最小入边的权值
- 此时得到的边权值称为 reduced cost
- 在 reduced cost
上面做最小有根树,得到的结果也是原权值上形成的最小有根树
- 根据上面的不等式,显然正确
Edmonds branching algorithm
- 算法思路
- reduced cost \(\to\) 遇到环则收缩环 \(\to\) reduced cost \(\to\) 收缩环 \(\to\cdots\)

- 算法给有根树加了更强的限制,对于收缩过程中的环,只允许有一条入边
- 实际有根树没有这个限制,如下图
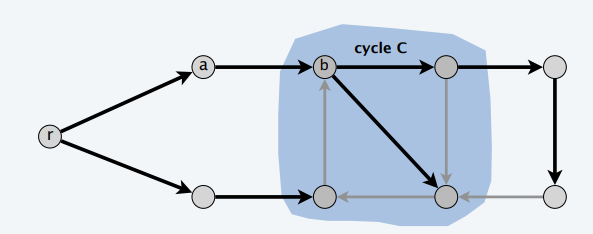
- 能被证明,这个限制条件没问题
定理
- \(C\) 不包含点 \(r\)(算法一开始便可以去除 \(r\) 的所有入边)

- 如果没有边进入 \(C\),因为是有根树 \(\Rightarrow\) 至少有一条边(假设不成立)
- 如果恰好有一条边进入 \(C\) \(\Rightarrow\) \({\color{red}\checkmark}\)
- 如果两条或者两条以上的边进入 \(C\)
\(\Rightarrow\)
可以转化为一条边,得到的还是最小有根树
- 假设 \(r\) 到 \(C\) 最近路径为 \(r\sim\cdots\sim a\sim b\),入边为 \((a,b)\)
- 除了 \((a,b)\),删除 \(C\) 上所有点的入边
- 包括除了 \((a,b)\) 之外的: \(C\) 的入边、\(C\) 内部连接各个结点的边
- 除了进入 \(b\) 的边,加上环 \(C\) 上的所有边
- 根据 \(\text{cost}(e)=0,\forall e\in
C\),得到的还是最小有根树
- 权不增
- 任意一点都只有一条入边
- 无有向环
证明
- [Chu–Liu 1965, Edmonds 1967]
- The greedy algorithm finds a min-cost arborescence
- 根据上面的引理已经很显然了
分析
- \(O(mn)\)
- 最多 \(n\) 次收缩点
- 找一个环开销 \(O(m)\)
- 将结果转换回去开销 \(O(m)\)
- 最多 \(n\) 次收缩点
其他算法
- [Gabow–Galil–Spencer–Tarjan 1985]
- There exists an \(O(m + n \log n)\) time algorithm to compute a min-cost arborescence.