算法设计与分析.04.贪心算法 (1)

Posted on Edited on In Views:
贪心算法分析策略，交换货币问题，区间调度，最低延迟调度，最优缓存策略

贪心算法

  • coin changing
  • interval scheduling
  • interval partitioning
  • scheduling to minimize lateness
  • optimal caching

贪心算法分析策略

  • Greedy algorithm stays ahead
    • 证明在每一步过后，贪心算法至少和其他算法一样好
  • Structural
    • 找到所有可行解都需要满足的数值性质，而贪心算法总能够达到临界值
  • Exchange argument
    • 把最优算法一步步变换到贪心算法的结果，在这个过程中不失其最优性

交换货币问题

  • 有不同面值的硬币，给定一个总数，计算最少使用的货币数量

Cashier′s algorithm

最优性

  • Cashier′s algorithm
    • 从大到小使用货币
  • 不是最优的
    • 硬币面值：1，4，5
    • 总和：8
    • 算法结果：5，1，1，1
    • 最优结果：4，4
  • 可能实际有解，但是算法无解
    • 硬币面值：7，8，9
    • 总和：15
    • 算法结果：9，？
    • 最优结果：8，7

美国货币是最优的

  • 硬币：penny(1)、nickel(5)、dime(10)、quarter(25)、dollar(100)
  • 限制条件：
1
2
3
4
penny         <= 4;
nickel        <= 1;
quarter       <= 3;
nickel + dime <= 2;
  • 证明
    • 对总数 \(x\) 进行归纳
    • 对于 \(c_{k}\le x<c_{k+1}\) 一定会取货币 \(k\)
      • 否则无解，如下图
        • Line 2：如果不使用 nickel，根据对 penny 的限制，最多只能够达到总数 4
        • Line 5：如果不使用 dollar，根据对其他硬币的限制，最多只能够达到总数 99
          • \(4+20+25*3=99\)
    • 此时转化为 \(x-c_{k}\) 的子问题

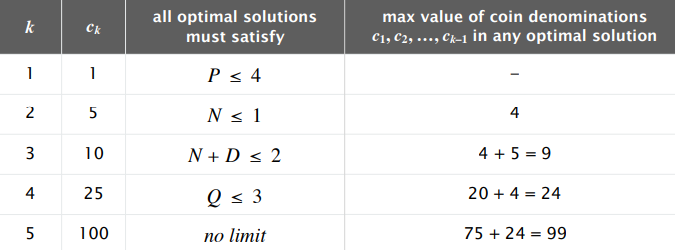
区间调度

  • 工作 \(j\) 开始于 \(s_j\) 结束于 \(f_j\)（开区间）
  • 工作 \(i,j\) 相容 \(\Leftrightarrow\) \((s_i,f_i)\cap(s_j,f_j)=\varnothing\)
    • compatible
  • Goal：找出最多相容的工作

算法分析

  • 排序后从前往后选
  • 按照开始时间升序：不是最优的
    • Earliest start time
1
2
------------
 --  --  --
  • 按照结束时间升序：最优的
    • Earliest finish time
  • 按照持续时间升序：不是最优的
    • Shortest interval
1
2
---- ----
   ---

EFTF

  • earliest-finish-time-first algorithm
  • \(O(n\log n)\)

最优性分析

  • 反证法
  • 假设不是最优的，算法得到的序列为 \(i_1,\cdots,i_k\)
    • 此时必然有 \(m<n\)
  • 设 \(r\) 是满足如下情况的的最大值
    • \(i_1=j_1,i_2=j_2,\cdots,i_r=j_r\)
  • 设 \(j_1,\cdots,j_m\) 是 \(k\) 最大的最优序列

  • 设 \(a=i_{r+1},b=j_{r+1},c=j_{r}=i_{r}\)
    • 根据贪心策略，\(f_{a}\le f_{b}\)
  • 如果 \(f_a=f_b\)，那么会有 \(s_a<s_b\)
    • 此时将最优策略中的 \(b=f_{r+1}\) 替换为 \(a=i_{r+1}\)，还是最优的，与序列 \(j\) 的最大 \(k\) 矛盾
  • 如果 \(f_a<f_b\)，根据相容性：\(f_{c}<=s_{a}<s_{b}\)，同样可以替换，矛盾

区间划分

  • 讲座 \(j\) 开始于 \(s_j\) 结束于 \(f_j\)，不同讲座不能共用教室，如果需要让所有的讲座按时开展，最少需要几间教室？

算法分析

  • 排序后从前往后选
  • 按照开始时间升序：最优的
    • Earliest start time

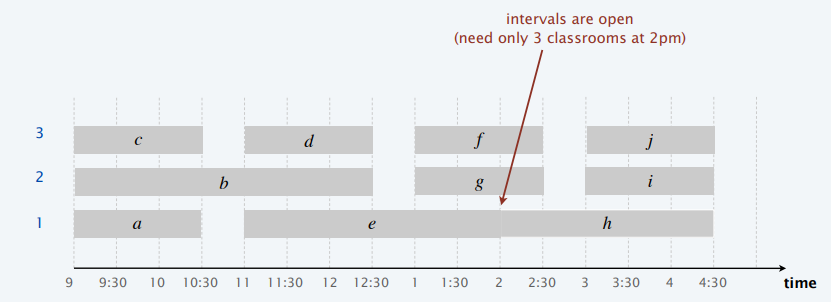
  • 按照结束时间升序：不是最优的
    • Earliest finish time

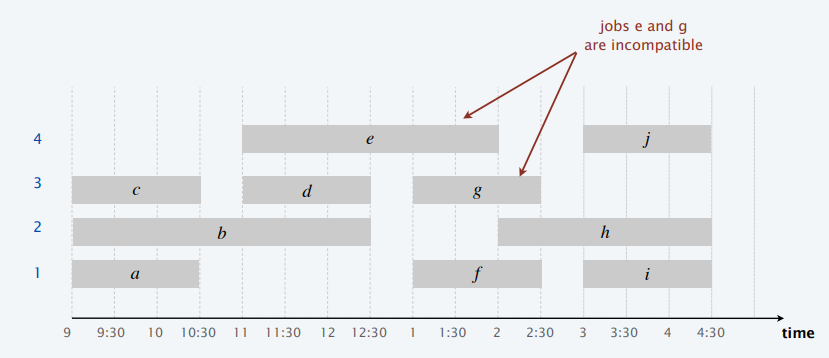
  • 按照持续时间升序：不是最优的
    • Shortest interval

ESTF

  • earliest-start-time-first algorithm
  • \(O(n\log n)\)

深度

  • The depth of a set of open intervals is the maximum number of intervals that contain any given point.
    • 同时开展讲座的最多门数
  • 观察：需要的教室数目 \(\ge\) 深度
    • 至少需要这么多

最优性分析

  • ESTF 算法不会将两门不相容的课放在同一间教室里
  • 设 d 表示 ESTF 算法使用的教室数目
  • 假设我们使用第 \(d\) 间教室的时候，调度讲座 \(j\)
  • 此时剩余 \(d-1\) 间教室都在使用，而且这些教室的开始时间都比 \(j\) 早
  • 也就是说，在时刻 \(s+\epsilon\)，有 \(d\) 门讲座同时开展
  • 注意此时，任意算法使用教室数目 \(\ge d\)
  • 最优性得证

最低延迟调度

  • scheduling to minimize lateness
  • 任务 \(j\) 耗时 \(t_j\) 截止时间 \(d_j\)
  • lateness：\(l_j\)
    • 如果任务 \(j\) 分配开始做的时间是 \(s_j\)，那么 \(l_j=\max\{0,s_j+t_j-d_j\}\)
  • Goal：调度使得 \(L=\max_j{l_j}\) 最小
  • 算法输入满足：\(d_1\le d_1\le\cdots\le d_n\)

算法分析

  • 按照处理时间升序
    • shortest processing time
  • 按照截止时间升序：最优
    • earliest deadline first（EDF）
  • 按照 \(d_j-t_j\) 升序
    • smallest slack

no idle time

  • 最优调度一定是没有空闲时间（idle time）的

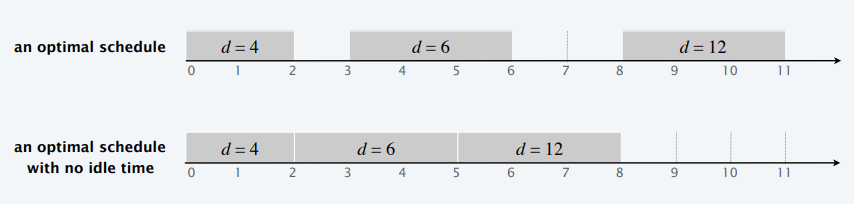
  • 去掉空闲时间，则转化为更优的调度
  • EDF 算法是没有空闲时间的

inversion

  • inversion：倒置（对）
    • 指对于某个调度 S，存在对 \((i, j),i<j\)，任务 \(j\) 被调度在 \(i\) 之前

  • EDF 是唯一不存在空闲时间、而且不存在倒置对的调度
  • 如果一个调度存在倒置对，那么一定存在相邻的倒置对（上图的 \(i,j\) 就是）
    • 反证法，假设最近的倒置对是 \(i,j,(i<j)\)，假设任务 \(j\) 之后的是任务 \(k\)
      • 对 \(j,k\) 大小进行分类讨论

  • 如果存在相邻倒置对，那么交换这连个任务的调度顺序，不会使的 \(L\) 增大
  • 证明：
    • 其他任务的 lateness 不变
    • 对于任务 \(i\)
      • \(d'_i=\max\{s_j+t_i-d_i,0\}\le\max\{s_i+t_i-d_i,0\}=d_i\)
    • 对于任务 \(j\)
      • 如果调度之后 \(l'_j=0\)，显然 \(L\) 没有增大
      • 如果调度之后 \(l'_j\ne0\)
        • \(l'_j=s_i+t_i-d_j\le s_i+t_i-d_i\le l_i\le L\)
        • 因此 \(L\) 没有增大

EDF

  • EDF 调度是最优的（因为不存在倒置对）
  • 反证法：假设调度 S' 是最优调度中倒置对最少的
    • 如果为 0，则就是 EDF
    • 如不为 0，则可以构造出倒置对更少的最优调度，矛盾

最优缓存策略

  • cache：大小为 \(k\)
  • 请求序列：\(d_1,d_1,\cdots,d_m\)
    • 已知的，offline
  • cache hit
  • cache miss（evictions）
  • 求一种缓存策略，使得 cache miss 次数最少

例子

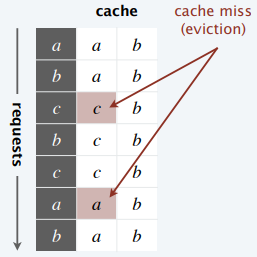
贪心算法

  • LIFO/FIFO
    • Evict item brought in least (most) recently
    • 访问顺序
  • LRU
    • Evict item whose most recent access was earliest
  • LFU
    • Evict item that was least frequently requested

最优离线算法

  • Farthest-in-future
    • 驱逐将来最晚访问的一个元素
  • [Bélády 1966] FF is optimal eviction schedule.

FF 最优性

reduced schedule

  • reduced schedule

    • d 进缓存当且仅当同时满足如下两种情况
      • 当前时刻请求 d
      • d 不在缓存中

  • 可以将一个 unreduced schedule 转变为 reduced schedule，同时不增加驱逐次数

    • 归纳法

  • 假设步骤 \(j\) 的时候，没有请求 \(d\)，便将 \(d\) 载入缓存，此时驱逐了 \(c\)（分类讨论）

  • \(d\) 不在缓存中

    • \(d\) evicted before next request for \(d\)
      • 不载入 \(d\)，驱逐次数减小 1
    • next request for \(d\) occurs before \(d\) is evicted
      • 直至请求 \(d\) 的时候再载入 \(d\)
      • 驱逐次数不变（甚至更少，中间请求了 \(c\)）

  • \(d\) 在缓存中

    • \(d\) evicted before it is needed.
      • 不载入 \(d\)，驱逐次数减小 1
    • \(d\) needed before it is evicted.
      • 直至请求 \(d\) 的时候再载入 \(d\)
      • 驱逐次数不变（甚至更少，中间请求了 \(c\)）

证明

  • 存在一个 reduced schedule（S） 和 FF 的驱逐次数相同
  • 归纳法
  • \(1\sim j\) 步执行结束之后，两种方法 cache 相同，考虑 \(j+1\) 步骤（分类讨论）
  • \(d\) 在 cache 中
  • \(d\) 不在 cache 中
    • 驱逐元素一样
    • 驱逐元素不一样，FF 驱逐 \(e\)，S 驱逐 \(f\)
      • 构造 S'，S‘ 和 S 除了在 \(j+1\) 驱逐了 \(e\) 之外和 S 完全一样
      • 在接下来的步骤中，S' 保持和 S 相同，直到需要请求 \(e/f\) 或者 S 驱逐了 \(e\)
      • 请求 \(e\)：不可能发生，根据 FF 的性质，\(f\) 的请求发生在 \(e\) 之前
      • 请求 \(f\)
        • 此时 S 中不包含 \(f\)（reduced schedule 性质）
        • 如果此时 S 驱逐 \(e\)，此时 S' 直接从 cache 中获取 \(e\)，S' 驱逐次数比 S 少 1
        • 如果此时 S 驱逐元素不是 \(e\)，此时 S' 驱逐 \(e'\) 获取 \(e\)，S' 驱逐次数和 S 相同
        • 上面两种行为的结果都使得 S 和 S' 的 cache 相同，之后让 S' 的行为和 S 一致，，此时调度 S' 的驱逐次数不必 S 多，接着将 S' 修改为 reduced schedule 即可（由于前 \(j+1\) 步骤满足 reduced schedule 的规则，因此可以保留前 \(j+1\) 不变，即和 FF 相同）
      • 驱逐了 \(e\)
        • S' 驱逐 \(f\) 即可，接着行为和 S 相同，然后转化为 reduce schedule 即可

在线算法

  • online：事先不知道请求序列
  • LRU 是 \(k\) 竞争的（\(k\)-competitive）
    • 对于任意一个请求序列 \(\sigma\) 满足：\(\text{LRU}(\sigma) ≤ k\cdot \text{FF}(\sigma) + k\)
  • Randomized marking is \(O(\log k)\)-competitive