算法设计与分析.03.图算法及其概念

Posted on Edited on In Views:
图算法及其概念，图的表示，连通性，拓扑排序

图

  • Graph

基本定义与应用

无向图

  • Undirected graphs
  • \(G=(V,E)\)
  • 结点/节点：nodes/vertices
  • 边：edges/arcs
  • \(n=\vert{V}\vert,m=\vert{E}\vert\)
  • \(degree(u)=\vert B\vert,B=\{v:edge(u,v)\in E\}\)

应用

graph node edge
communication telephone, computer fiber optic cable
circuit gate, register, processor wire
mechanical joint rod, beam, spring
financial stock, currency transactions
transportation street intersection, airport highway, airway route
internet class C network connection
game board position
social relationship person, actor friendship, movie cast
neural network neuron synapse
protein network protein protein-protein interaction
molecule atom bond

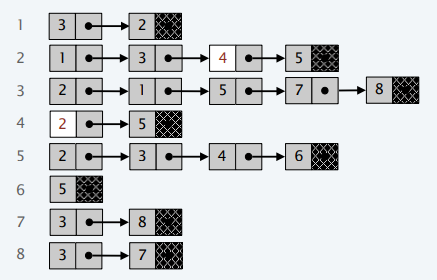
图的表示

  • 无向图如下

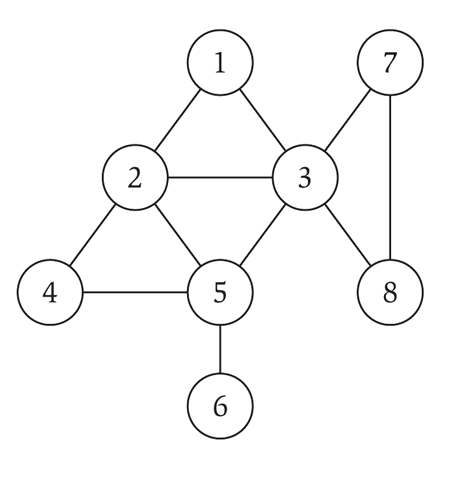
邻接矩阵

  • adjacency matrix

邻接表

  • adjacency lists

路径与连通性

  • paths and connectivity
  • 简单路径（simple）
    • 路径上结点都不相同
  • 连通的（connected）
    • 任意两个节点之间都存在路径

环

  • cycle
  • 首尾结点相同的路径，长度大于等于 2
  • 简单环（simple）
    • 除了首尾结点之外，其他结点两两不同

树

  • tree
  • 无向图：连通图 + 无环
  • 如下 3 个结论，任意两个都可以推导得到剩下一个
    • G is connected.
    • G does not contain a cycle.
    • G has n – 1 edges.

有根树

  • rooted tree
    • 树确定根，确定父子关系

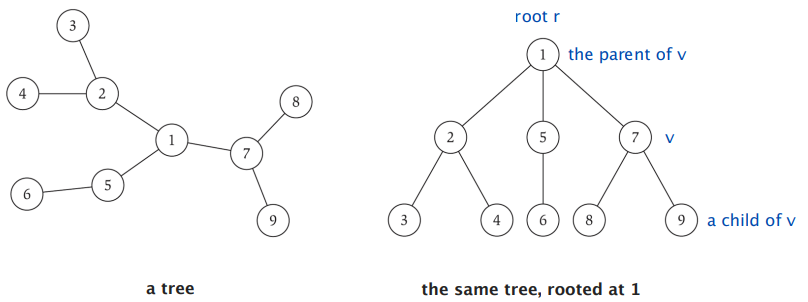
应用

  • Phylogeny trees：系统发育树
  • GUI containment hierarchy：GUI 层次结构树

图的连通性与遍历

连通性

  • s-t connectivity problem
    • 是否存在路径
  • s-t shortest path problem
    • 最短路径

BFS

  • Breadth-first search：宽度优先遍历
    • Explore outward from s in all possible directions, adding nodes one “layer” at a time.

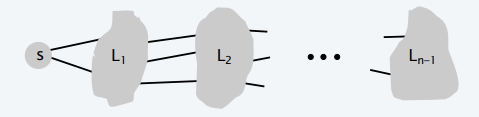
  • 性质
    • 如果 s-t 存在路径，则 t 一定出现在某一层上
    • 如果 (x, y) 是图上的一条边，则它们深度最多相差 1
  • 时间复杂度
    • 邻接表：\(O(m+n)\)
    • 无向图：每一条边都会被检查 2 次

连通分支

  • Connected component
    • Find all nodes reachable from s.

Flood Fill

  • 画图：油漆桶工具

Testing bipartiteness

二部图

  • 二部图/二分图（Bipartite graphs）

  • 二部图具有很好的性质
    • 简化问题：匹配
    • 可操作：独立集
  • 二部图不存在奇数长度的环

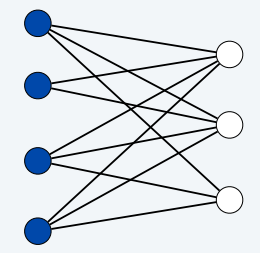
引理

  • G 是连通图，\(L_0,\cdots,L_k\) 是 BFS 形成的层级

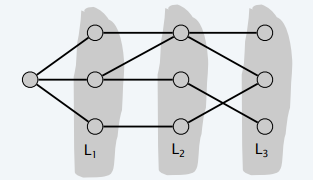
  • 如果同层之内没有边，则是二部图
    • 回顾：BFS 形成的层次结构，edge(u, v) 的两个结点层数最多相差 1
  • 否则存在奇数环
    • z 表示 u,v 的最近公共祖先
    • \(z-L_{i+1}-\cdots-L_{j-1}-u-v-L_{j-1}-\cdots-L_{i+1}-z\)
    • 边数：\(2(i-j+2)+1\)

推论

  • 无向图 G 是二部图当且仅当图 G 不含有奇数长度的环
  • 不包含奇回路 \(\Rightarrow\) 上面奇数层级为一部，偶数层级为一部，证明部的内部没有点相邻
  • G 是二部图 \(\Rightarrow\) 反证法，假设存在奇回路，则无法二着色

有向图中的连通性

  • 有向图（directed graph）
  • 有向边：edge(u,v) 表示 \(u\to v\)
  • 应用
    • 互联网中的超链接
    • 交通路网
    • 食物网

图搜索

  • Directed reachability
    • 找到 s 可达的所有顶点
  • Directed s\(\to\)t shortest path problem

强连通性

  • strong connectivity
  • 一个有向图是强连通的 \(\Leftrightarrow\) 任意两点相互可达
  • 推论：
    • s 是 G 中任意一点
      • G 是强连通的 \(\Leftrightarrow\) 任意一点可达 s，而且 s 可达任意一点
  • 根据推论判断一个图是否强连通
    • 选择任意点 s
      • 在 G 和 G‘ 上判断 s 能够到达任意点
      • G'：将 G 上的所有边逆向之后得到的新图
    • \(O(m+n)\)

强连通分量

  • Strong components
  • 最大的互相可达的顶点集合

  • Tarjan 算法：\(O(m+n)\)
    • 1972

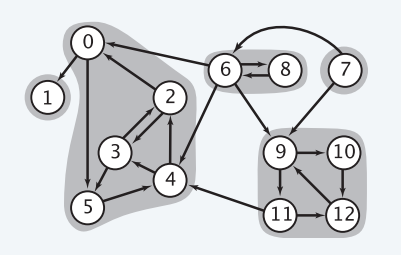
有向无环图与拓扑排序

  • 有向无环图
    • Directed acyclic graphs
    • DAG
  • 拓扑排序
    • topological ordering

DAG

  • 有向图 + 无环
  • 拓扑序：节点的一个排序 \(v_1,v_2,\cdots,v_n\)，是的不存在一条边 \(edge(v_i,v_j),i>j\)
  • Precedence constraints：优先级的约束
    • 选课的先修课
    • 编译的模块顺序
    • 流水线工作
  • 有向图 G 是 DAG \(\Rightarrow\) G 存在一个结点没有入边
    • 反证法，否则有环
  • 有向图 G 是 DAG \(\Leftrightarrow\) G 存在一个拓扑排序
    • \(\Leftarrow\)：反证法，假设有环则无拓扑排序
    • \(\Rightarrow\)：归纳法，根据上面的定理
  • 找到一个拓扑排序
    • 依次取没有入边的点（除去它的相关边）
    • \(O(m+n)\)