GAMES103.王华民.11.Incompressible Fluid Dynamics and Eulerian Fluids(2)
Navier-Stokes 方程
- Low-speed, Incompressible, Viscous Navier Stokes’ equations
- 低速、不可压缩、带有粘滞性的流体
NS 方程
- 流体速度场的更新:NS 方程
- 不可压缩条件(Incompressibility)
\[ \nabla\cdot\mathbf{u}=0 \]
- 动量(Momentum)
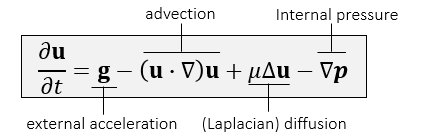
- 如何求解上述偏微分方程?
- Method of Characteristics:拆分 PDE 的不同部分,分步求解

求解 NS 方程
S1-External Acceleration
- 在这里我们先假设外部加速度只有重力加速度
\[ \dfrac{\partial{\mathbf{u}}}{\partial{t}}=\mathbf{g} \]
- 对所有的墙更新 \(u,v\)
\[ v_{i,j}^{new}\leftarrow v_{i,j}+\Delta tg \]
S2-Advection
\[ \dfrac{\partial{\mathbf{u}}}{\partial{t}}=-(\mathbf{u}\cdot\nabla)\mathbf{u} \]
- 展开如下
\[ (\mathbf{u}\cdot\nabla)\mathbf{u}= \begin{pmatrix} u\cdot\dfrac{\partial{u}}{\partial{x}} + v\cdot\dfrac{\partial{u}}{\partial{y}}\\ u\cdot\dfrac{\partial{v}}{\partial{x}} + v\cdot\dfrac{\partial{v}}{\partial{y}}\\ \end{pmatrix} \]
- 求解方式1:计算得到右边的值,然后类似于 S1 的方式求解
- 不稳定
- 原因:当时间步长 \(\Delta t\) 比较大的时候,估算得到的一阶导数不准确
advection
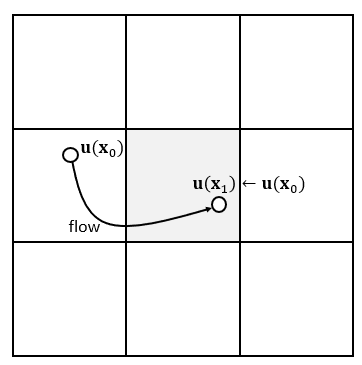
- 由于水分子的流动,\(t\) 时刻网格内的水分子不再是 \(t-\Delta t\) 时刻的水分子,因此需要用新的水分子的速度替换掉原来的速度
- 如上图所示,\(\mathbf{x}_1\) 位置的水分子是上一时刻在 \(\mathbf{x}_0\) 位置的水分子,因此需要使用 \(\mathbf{x}_0\) 位置水分子的速度 \(\mathbf{u}(\mathbf{x}_1)\) 替换掉 \(\mathbf{u}(\mathbf{x}_1)\)
- 拉格朗日方法没有这个问题,因为本身就是定义在粒子上的,这一时刻的粒子和上一时刻的粒子是同一个
Semi-Lagrangion Method
- 半拉格朗日方法
- 思路:对于一个点 \(\mathbf{x}_0\),推断上一个时刻这个点的位置
\(\mathbf{x}_1\),然后用 \(\mathbf{x}_1\) 的速度替换掉即可
- 下面的 comupte 就是利用双线性插值计算
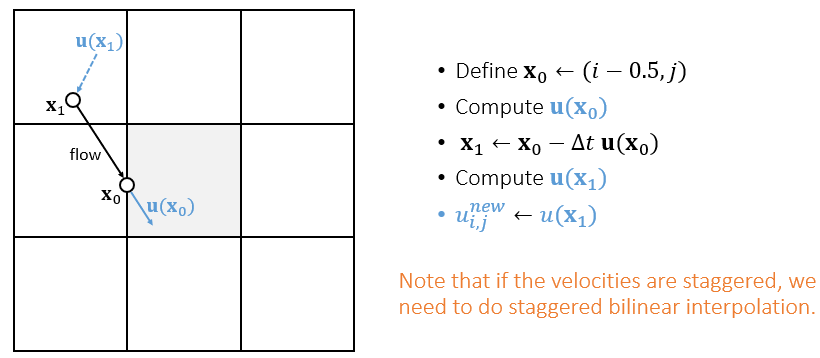
- 对于交错网格,\(u,v\) 分开计算
- 细分:小步长精度更高
- 数值方法
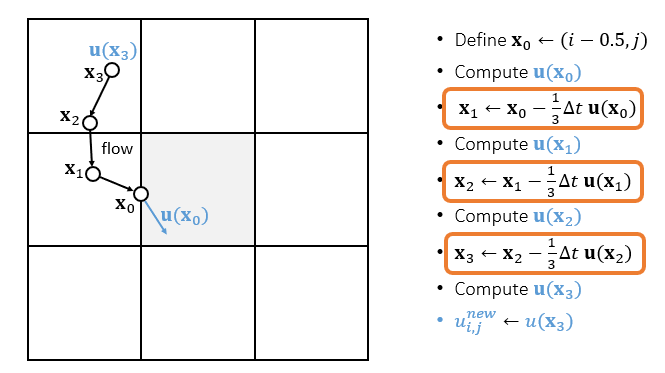
- 边界问题:倒推之后发现在边界怎么办?
- clamp,不让它越界
- 是个稳定的方法,但是大的步长会有误差
- 误差表现为模糊(源自插值)
S3-Diffusion
\[ \dfrac{\partial{\mathbf{u}}}{\partial{t}}=\mu\Delta\mathbf{u} \]
- 分别对 \(u,v\) 做拉普拉斯平滑
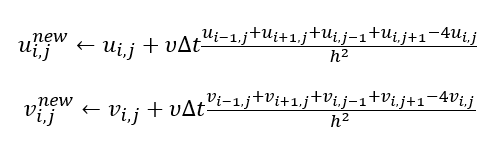
- 大步长可能会不稳定(\(v\Delta t\) 太大)
- 使用小步长计算
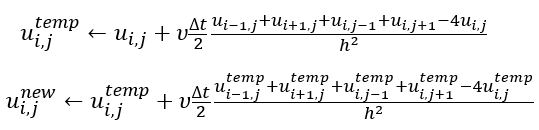
- 可以使用隐式积分来做
- 比较复杂,利用小步长也能做出类似效果
S4-Pressure Projection
- 利用压强进行更新
\[ \dfrac{\partial{\mathbf{u}}}{\partial{t}}=-\nabla\mathbf{p} \]
- 压强定义在网格中心,因此表达起来很方便
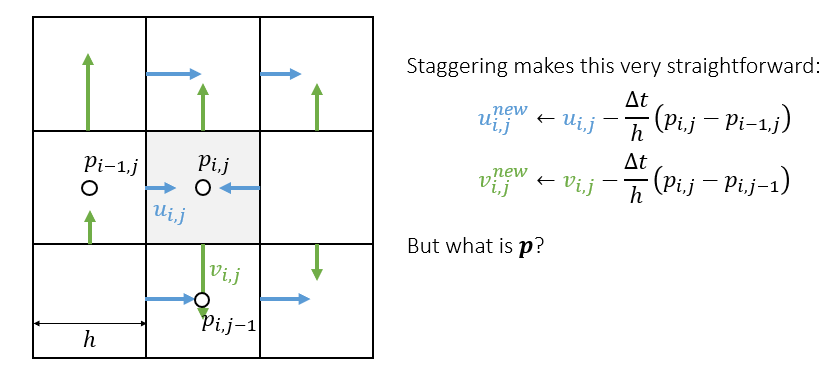
压强
- 如何计算/更新 \(\mathbf{p}\)
- 压强产生的原因:流体是不可压缩的
- 因此从散度为 0 开始推导(\(\Delta\mathbf{u}^{new}=0\))

- 因此得到方程组,把所有的方程组联立求解线性系统
- 边界条件
- Dirichlet boundary (open) \(p_{i-1,j}=P\)
- Neumann boundary (close) \(p_{i-1,j}=p_{i,j}\)
- 真实的墙
- 求解得到 \(p\) 之后便能够计算得到速度 \(u,v\)
- pressure projection
- 利用压强对速度进行投影,使得更新之后的速度满足不可压缩的条件
参考实现
- Jos Stam. 1999. Stable Fluids. TOG (SIGGRAPH).
Air and Smoke
烟雾模拟
- 烟雾模拟的两个步骤
- Step 1:更新速度
- Step 2:更新其他物理量
- 烟雾:颜色、密度
- 可以利用 Semi-Lagrangian 的方法更新,理解和 advection 类似,这些物理量都是会被例子带着走的,因此可以通过找到之前的位置,使这个位置的物理量进行更新
- 边界
- 开放空间:Dirichlet boundaries
- 密闭空间(container):Neumann boundaries
水的模拟
- 水的模拟比较复杂
- 水是有形状的,我们实际上模拟的是水和空气的表面,但是我们实际上只会模拟水而不是一起模拟水和空气
- 水在整个过程中并不会占满整个空间,只会占据一部分空间,如何表达部分空间的占用?
- 水有自己一套表达的方式
表达方式
- Volume-of-fluid(VoF):体积的表达方式
- 划分为小格子,然后告诉你这个格子中被液体占据的百分比
- 不精准
- SDF:有向距离场
- 保存到水面的距离
更新方式
- Semi-Lagrangian
- Level set:对距离函数进行更新的一种方法
- 问题:volume loss issue
- 上面两种方法在模拟过程中水的体积会发生改变,因此需要修正
导出数据
- 如何将得到的体数据导出为 mesh 用于渲染
- marching cube
实现
流体仿真书籍
- Level Set Methods and Dynamic Implicit Surfaces.
- Osher and Fedkiw.