算法设计与分析.02.算法分析

Posted on Edited on In Views:
时间复杂度分析与表示

算法分析

引子

计算模型

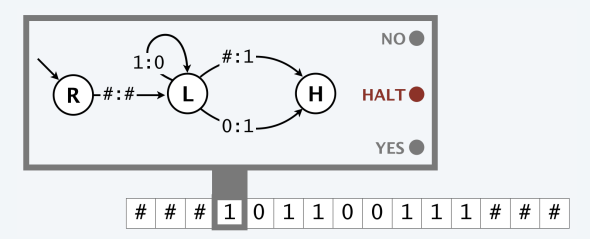
  • 图灵机
    • Running time：Number of steps
    • Memory：Number of tape cells utilized

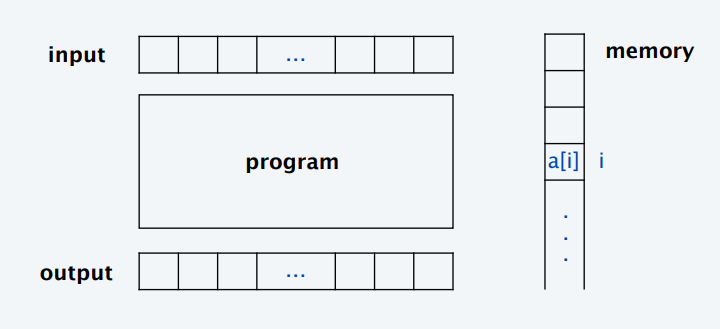
  • Word RAM
    • 执行指令：简单操作、复杂操作（简单操作的集合）、存储访问
    • 时间：基本操作个数
    • 空间：占用内存

  • 多项式运行时间
    • efficient
  • 算法
    • Brute Force（暴力）
  • 分析方式
    • 最好/最差情况
    • 平均情况：随机算法
    • 平摊分析（Amortized Analysis）

渐进分析

表示法

  • 大 \(O\) 表示法

\[ f(n)=O(g(n))\Longleftrightarrow0\le f(n)\le c\cdot g(n),\exists c>0,\forall n\ge n_0 \]

  • 大 \(\Omega\) 表示法

\[ f(n)=\Omega (g(n))\Longleftrightarrow f(n)\ge c\cdot g(n)\ge 0,\exists c>0,\forall n\ge n_0 \]

  • 大 \(\Theta\) 表示法

\[ f(n)=\Theta (g(n))\Longleftrightarrow 0\le c_1\cdot g(n)\le f(n)\le c_2\cdot g(n)\ge 0,\exists c_1,c_2>0,\forall n\ge n_0 \]

极限与渐进分析

\[ \lim_{n\to\infty}\dfrac{f(n)}{g(n)}=c,0<c<\infty\Longleftrightarrow f(n)=\Theta(g(n)) \]

\[ \lim_{n\to\infty}\dfrac{f(n)}{g(n)}=0\Longleftrightarrow f(n)=O(g(n)),f(n) \ne\Omega(g(n)) \]

\[ \lim_{n\to\infty}\dfrac{f(n)}{g(n)}=\infty\Longleftrightarrow f(n)=\Omega(g(n)),f(n) \ne O(g(n)) \]

极限

\[ \lim_{n\to\infty}\dfrac{\log_an}{n^d}=0,\forall a>1,\forall d>0 \]

\[ \lim_{n\to\infty}\dfrac{n^d}{r^n}=0,\forall r>1,\forall d>0 \]

  • Stirling’s formula

\[ n!\sim\sqrt{2\pi n}\left(\dfrac{n}{e}\right)^{n} \]

\[ n!=2^{\Theta(n\log n)} \]

多变量

  • 大 \(O\) 表示法

\[ f(m,n)=O(g(m,n))\Longleftrightarrow0\le f(m,n)\le c\cdot g(m,n),\exists c>0,\forall n\ge n_0,\forall m\ge m_0 \]

例子

常数时间

  • Constant time
  • \(O(1)\)
  • 基本操作

线性时间

  • Linear time

  • \(O(n)\)

  • TARGET-SUM

    • Given a sorted array of n distinct integers and an integer T, find two that sum to exactly T
    • 双指针法
      • 另一种理解，数组 a，数组 b，其中 b[i] = target - a[i]
      • 此时转化为判断 a 和 b 中是否有相同元素

对数时间

  • Logarithmic time
  • \(O(\log n)\)
  • 有序数组二分查找
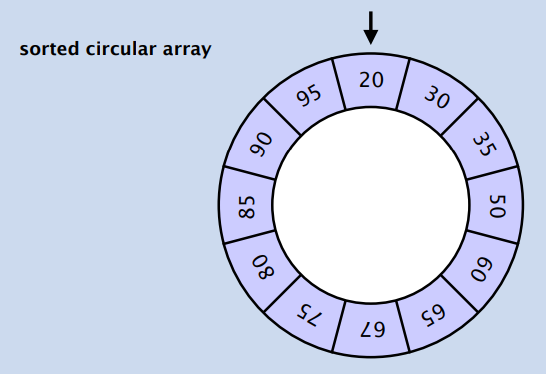
  • SEARCH IN A SORTED ROTATED ARRAY
    • 有序环状数组

线性对数时间

  • Linearithmic time
    • linearithmic
  • \(O(n\log n)\)
  • 归并排序：Mergesort
  • LARGEST EMPTY INTERVAL
    • 先排序？

平方时间

  • Quadratic time
  • \(O(n^2)\)
  • 最近点对问题：Closest pair of points
    • 枚举所有点对

立方时间

  • Cubic time
  • \(O(n^3)\)
  • 3-Sum：求满足和为给定数的三元组个数
    • 暴力枚举
    • \(O(n^2)\)：排序 + 双指针

多项式时间

  • Polynomial time
  • \(O(n^k),k>0\)
  • 独立集：Independent set of size k.
    • Given a graph, find k nodes such that no two are joined by an edge.
    • 枚举所有大小为 k 的子集，然后判断是否为独立集（枚举点对）
    • \(k^2{n\choose k}\le\dfrac{n^k}{k!}k^2\le n^k\)
    • \(O(n^k)\)

指数时间

  • Exponential time
  • \(O(2^{t}),t=n^k,k>0\)
  • 最大独立集（Independent set）
    • Given a graph, find independent set of max cardinality
    • 枚举所有的子集，然后判断是否为独立集
      • 子集数目：\(2^n\)
  • 旅行商问题（Euclidean TSP）
    • Given n points in the plane, find a tour of minimum length.
    • 枚举所有的排列，然后计算出距离之和
    • 排列数：\(n!\)
    • \(O(n\cdot n!)\)
      • \(n!=2^{\Theta(n\log n)}\)