算法设计与分析.01.稳定匹配算法

Posted on Edited on In Views:
Stable Matching，稳定匹配算法

Stable Matching

问题描述

  • 给定一组医院 hospitals 和学生 students，每个医院对学生都有一个偏好列表，每个学生对医院也都有一个偏好列表，求一个稳定匹配 stable matching

概念

Matching

  • 一个 h 最多只能和一个 s 匹配，一个 s 最多只能和一个 h 匹配

Perfect matching

  • \(\vert{M}\vert=\vert{H}\vert=\vert{S}\vert=n\)

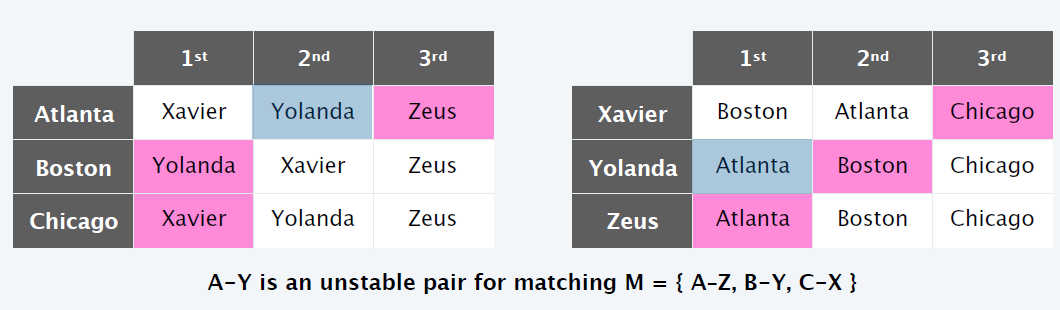
Unstable pair

  • 当 h - s 满足如下条件的时候，被称为 unstable pair
    • h 相较于现在的匹配学生，更喜欢 s
    • s 相较于现在的匹配医院，更喜欢 h
  • 例子：A - Y

Stable assignment

  • 不存在 unstable pair

Stable matching

  • perfect matching with no unstable pairs

Stable matching problem

  • 给定一组医院和学生（数目都为 n），每个医院对所有学生都有一个偏好列表，每个学生对所有医院也都有一个偏好列表，求一个稳定匹配

Stable roommate problem

  • 2n 个人，每个人对剩下的 2n-1 个人进行偏好排序
  • 根据这个偏好列表，找出一个稳定匹配
  • 不一定存在

Gale–Shapley algorithm

算法输入

  • n 个医院，n 个学生
  • 每一个医院对于 n 个学生的一个偏好列表，每一个学生对于 n 个医院的一个偏好列表

算法流程

正确性：会终止

  • 医院按照偏好列表降序选择学生
  • 学生一旦被选中之后，会一直处于匹配状态
    • 只会 trades up
  • 最外层的 WHILE 循环最多执行 \(n^2\) 次

正确性：perfect matching

  • 算法输出是一个匹配
    • 每个医院只会选择一个学生，每个学生只会选择一个医院
  • 所有医院都被匹配上了
    • 反证法：如果没有被匹配上，算法不会结束

  • 所有学生都被匹配上了
    • 计数：匹配 + 所有医院都被匹配上了

正确性：stability

  • 不存在 unstable pair
    • 假设存在一个不在匹配 M 中的 pair h-s，然后证明这不是非稳定对
  • 分类
    • h 已经选择过 s：根据 trade up，h-s 不是非稳定对
    • h 没有选择过 s：根据优先级，当前匹配 h-s1 优先级更高，h-s 不是非稳定对

结论

  • [Gale–Shapley 1962]
  • The Gale–Shapley algorithm guarantees to find a stable matching for any problem instance.

Hospital optimality

  • GS 算法是 hospital optimality 的
  • 对于下面的这个例子，存在两个稳定匹配，GS 算法会选择对于医院来说的最优解

  • All executions of Gale–Shapley yield hospital-optimality assignment

valid partner

  • 如果在某一个稳定匹配中存在匹配对 h-s，那么称 s 是 h 的 valid partner（可行伙伴）

证明

  • 反证法
  • 假设存在一个医院匹配上了一个不是最佳可行伙伴的学生（ GS 算法的过程中被最佳可性伙伴拒绝了）
  • 因为对于医院来说，是降序选取学生，此时也就是说存在某个医院在 GS 算法的过程中被他的某个可行伙伴拒绝了
  • 假设 h 是第一个满足上面条件的医院，假设 s 是第一个拒绝 h 的可行伙伴
  • 假设稳定匹配 M 中包含 h-s（接下证明 M 中存在不稳定对）
  • 当 GS 算法的过程中 s 拒绝 h 之后，匹配上的医院称为 h'，在 M 中 h' 的匹配对称为 s'
    • 于是有：s prefers hʹ to h
  • 根据上面的第一个的性质，算法执行到 s 拒绝 h 时，h' 没有被他的可行伙伴拒绝过
  • 也就是说，h' 先选择了 s，再选择了 s'
    • 于是有：h' prefers s to s'
  • 存在不稳定对 h'-s，与稳定匹配 M 矛盾

Student pessimality

  • 相应而言，GS 算法是 student pessimality 的
  • 类似的证明如下

扩展

  • Extension 1：Some agents declare others as unacceptable.
  • Extension 2：Some hospitals have more than one position.
  • Extension 3：Unequal number of positions and students.

GS 算法实现

  • \(\Theta(n^2)\)
  • 医院/学生索引：\(1\sim n\)
  • 维护结果数组 \(\text{hospital}[n],\text{student}[n]\)
    • 匹配：h - s 则 \(\text{hospital}[h]=s,\text{student}[s]=h\)
    • 未匹配：\(-1\)
  • 对每个医院维护一个 proposal list（链表或者数组）
  • 对每一个学生维护一个数组 \(\text{rank}[n]\)
    • \(\text{rank}[h]=k\) 表示医院 \(h\) 是该学生的第 \(k\) 个选择（优先级为 \(k\) ）
    • 预处理：\(\Omega(n^2)\)