GAMES103.王华民.11.Incompressible Fluid Dynamics and Eulerian Fluids
网格表示和有限差分
- A Grid Representation and Finite Differencing
- Incompressible, Viscous Navier Stokes’ equations
- 不可压缩、带有粘滞性的流体
- 空气(air)、液体(liquid)
规则网格表示
regular grid representation
在不做简化的前提下,模拟二维的流体,需要使用一个二维数组来表示
每一个格子都是一样大的正方形
每一个网格里可以定义一些物理量,表示网格中心的性质
- 标量:标量场
- Density/color、Pressure、Temperature
- 矢量:矢量场
- Velocities
- 标量:标量场
利用网格的离散性,容易实现计算导数、进行微分(差分)计算
中心差分
- 是 2 阶的
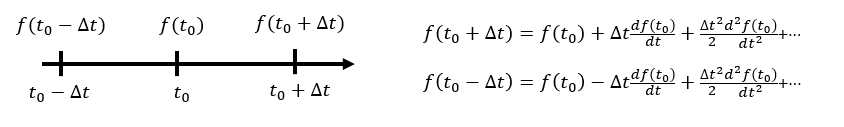
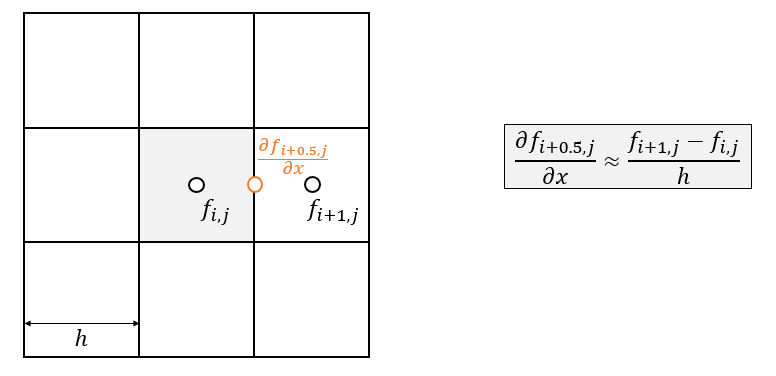
- 网格表示利于实现差分计算
- 从 1 阶导数到 2 阶导数
- 先计算 1 阶导数,再计算 2 阶导数
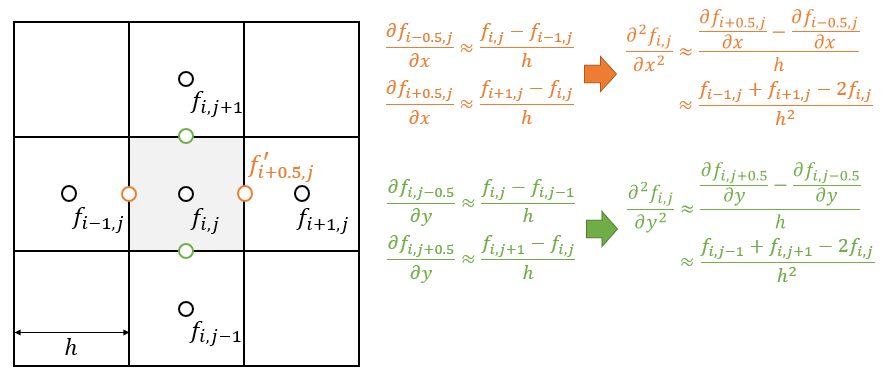
- 拉普拉斯算子
\[ \Delta f_{i,j}=\dfrac{\partial^2{f_{i,j}}}{\partial{x^2}}+\dfrac{\partial^2{f_{i,j}}}{\partial{y^2}} \approx\dfrac{f_{i-1,j}+f_{i+1,j}+f_{i,j-1}+f_{i,j+1}-4f_{i,j}}{h^2} \]
边界条件
- A Dirichlet boundary:\(f_{i-1,j}=C\)
- A Neumann boundary:边界和邻近边界的点具有某种关系
- 例:\(f_{i-1,j}=f_{i,j}\)
拉普拉斯方程
- \(\Delta f=0\)
\[ f_{i-1,j}+f_{i+1,j}+f_{i,j-1}+f_{i,j+1}-4f_{i,j}=0 \]
- 整个场上的任意点都满足这个条件
- 离散化则表示每一个网格都得满足拉普拉斯方程
- 边界条件中至少得有一个是 Dirichlet 边界条件,不能都是 Neumann 边界
- 如果全是 Neumann 边界,则问题会有无穷多个解
- 对于一个合理解,每一个点都加上一个常数 C,则还是合理解
- 求解拉普拉斯方程:Jacobi

- 拉普拉斯平滑:Laplacian Smoothing
- 直观理解:把当前点和邻居的点做平均
扩散
- 应用拉普拉斯平滑的过程,在仿真里面称为平滑
中心差分的问题
- 计算得到的一阶导数没有定义在网格的中心点上(计算出来的值是在边界上的)
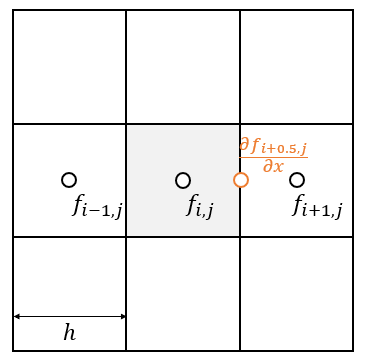
- 利用 \(f_{i+1,j},f_{i-1,j}\) 计算
\(\dfrac{\partial{f_{i,j}}}{\partial{x}}\)
- 有点奇怪,对于当前点的一阶导数计算竟然没有用到这个点本身的值
- 解决方案:没有必要把所有的变量都定义在网格中心,可以把一部分变量定义在墙(faces)上
Staggered Grid
- 交错网格
- 把一些物理量定义在墙上
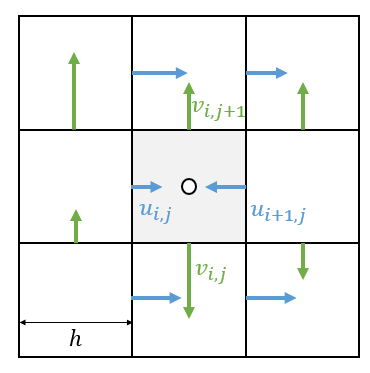
- 速度
- 把 x 方向的速度(u)定义在竖直的墙上
- 把 y 方向的速度(v)定义在水平的墙上
- 这样的定义可以把速度理解为流速:单位时间通过墙的液体量
- 在流体中很常见
- 应用:计算格子的净流出量
\[ (u_{i+1,j}+v_{i,j+1}-u_{i,j}-v_{i,j})\cdot\Delta{t} \]
- 好处:很直观的表示水流的变换
Divergence-Free Condition
- 不可压缩流体:每一个点的散度为 0
\[ \begin{aligned} \nabla\cdot\mathbf{u}_{i,j}&=0\\ &=\dfrac{\partial{u_{i,j}}}{\partial{x}}+\dfrac{\partial{v_{i,j}}}{\partial{y}}\\ &=\dfrac{u_{i+1,j}-u_{i,j}}{h}+\dfrac{v_{i,j+1}-v_{i,j}}{h}\\ \end{aligned} \]
- 每一个网格的净流入、净流出为 0
\[ u_{i+1,j}+v_{i,j+1}-u_{i,j}-v_{i,j}=0 \]
Bilinear Interlation
- 双线性插值
- 定义在网格中心的物理量
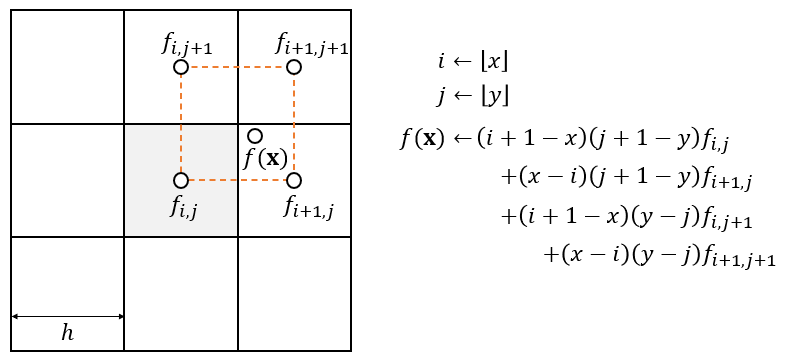
- 对定义在墙上的物理量进行插值
- 类似