NEE、MIS(多重重要性采样)

Posted on Edited on In Views:
NEE(Next Event Estimation)、MIS(Multiple Importance Sampling，多种重要性采样)

NEE

概念

  • NEE 的概念非常简单，就是在做积分的时候，将直接光照和间接光照区分开
    • 相当于分块积分

\[ \begin{aligned} I&=\int_{\Omega}g(X)\mathrm{d}\mu(X)\\ &=\int_{\Omega_1}g(X)\mathrm{d}\mu(X)+\int_{\Omega_2}g(X)\mathrm{d}\mu(X)\\ \end{aligned} \]

\[ \Omega_1\cap\Omega_2=\emptyset,\Omega_1\cup\Omega_1=\Omega \]

直接光照采样

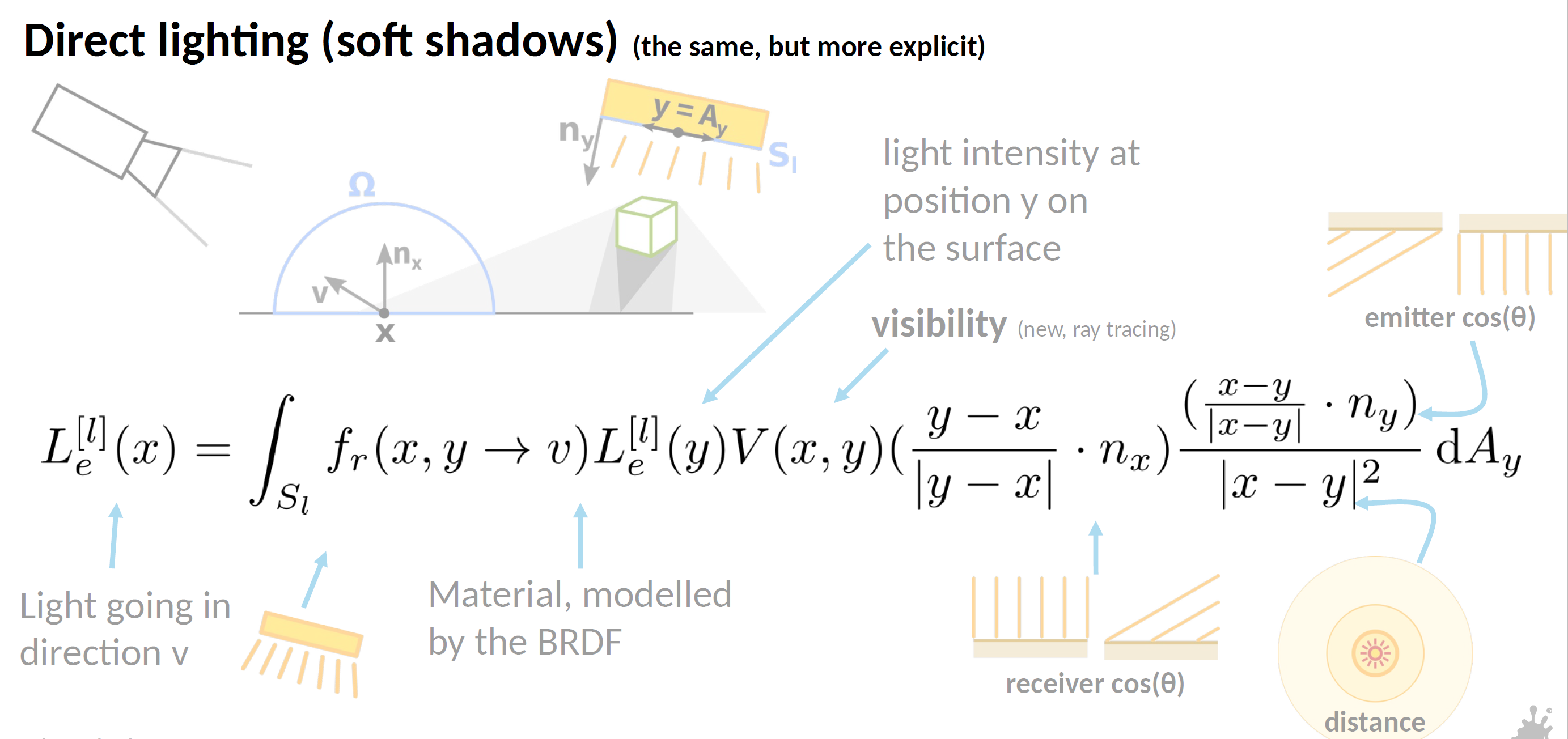
  • 这里的一个细节，需要将对光源的采样转化为对立体角的采样

算法流程

  • 首先在光源上采样，计算出贡献
  • 计算可见性，如果不可见，则计算得到的值为 0

实现

结果

  • 结果肯定是有偏的，因为只有 1-bounce 的光路，需要配合其他方法
    • 因为积分区域没有覆盖整个 BRDF 的定义域

NEE

  • 总体的思路是这样的

实现1

  • 在 path tracing 的框架中，每次求某一个点的 radiance 的时候，我们做两次采样，分别计算直接光照的和间接光照
  • 重复计算问题

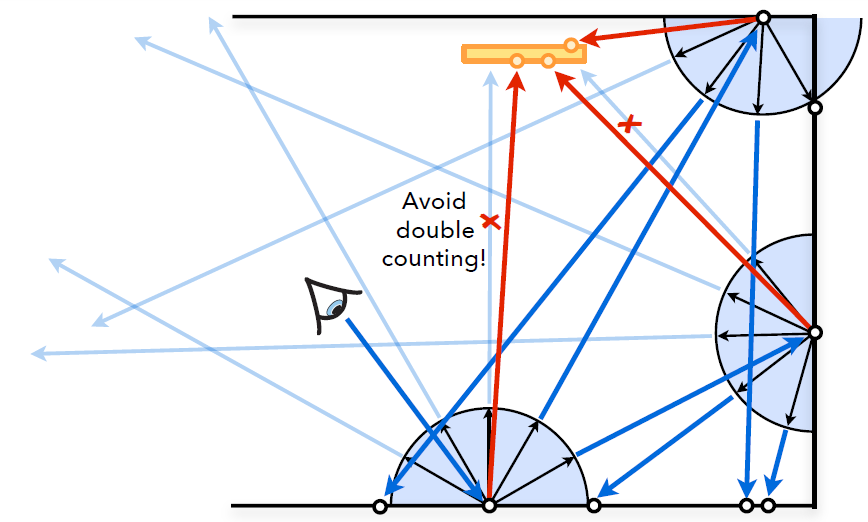
  • 直接光照采样，就和上面一样
    • 光源上采样一个位置，判断可见性，计算贡献值
  • 间接光照采样
    • 如果直接按照 BSDF 采样，那么结果是有偏的（太亮了）
    • 按照 BSDF 采样，这里的积分区域包含了上面光源的积分区域，导致重复计算
    • PPT 上给的一个实现，将第一次 bounce 之后的间接光照减半

  • 这种实现是无偏的吗？
    • 感觉不是无偏的

实现 2

  • 直接分离光照来源
    • 只有在直接光照采样的部分打到光源，才返回光源的 emission
    • 如果在间接光照采样的部分打到光源，返回 0
  • 这是无偏的
    • 所有路径都会被计算，且只会被计算一次

  • 另外一种写法
    • 镜面特殊处理，因为镜面没有直接光源采样（采不到）

问题

  • 我们使用 NEE 的原因是认识对光源采样比按照 BSDF 采样要好
  • 实际上对光源采样也会有问题
    • 不能很好的采样大光源

  • BSDF：能够较好采样大光源，对小光源采样差
  • 采样光源：能够较好采样小光源，对大光源采样差
  • 原因如下
    • 对于大光源，直接采样光源（面积）的范围比采样 BSDF（立体角）更大
    • 可以理解为立体角是面积采样的 Stratified Sampling
      • 面积采样有很多无效采样，例如一小部分面积内部可能一样

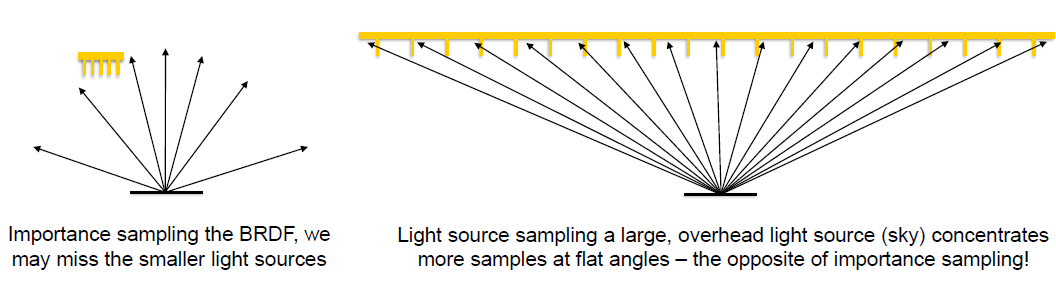
经典老图

  • Sampling the BRDF

  • A combination of samples from (a) and (b)

MIS

  • Multiple Importance Sampling
    • 多种重要性采样
  • 课件
  • 结合多种采样方式，更准确地说，结合多个 pdf

理论

  • 如果 \(\sum_{i=1}^{n}w_i=1\)
    • \(X_{i,j}\) 表示使用第 \(i\) 种采样方案采样到的第 \(j\) 个样本
    • \(p_i(X_{i,j})\) 表示这个方向在第 \(i\) 个 pdf 中的返回值

\[ F_i=\sum_{j=1}^{n_i}w_{i}(X_{i,j})\dfrac{f(X_{i,j})}{p_i(X_{i,j})} \]

\[ F=\sum_{i=1}^{n}\dfrac{1}{n_i}F_i \]

  • 注意 \(w_i(x)\) 和 \(x\) 相关，不能够将其从积分号中提出来

\[ \begin{aligned} E[F] &=\sum_{i=1}^{n}\dfrac{1}{n_i}E(F_i)\\ &=\sum_{i=1}^{n}\dfrac{1}{n_i}\int_{\Omega}\sum_{j=1}^{n_i}w_{i}(x)\dfrac{f(x)}{p_i(x)}p_{i}(x)\;\mathrm{d}\mu(x)\\ &=\sum_{i=1}^{n}\dfrac{1}{n_i}\int_{\Omega}\sum_{j=1}^{n_i}w_{i}(x)f(x)\;\mathrm{d}\mu(x)\\ &=\sum_{i=1}^{n}\int_{\Omega}\dfrac{1}{n_i}\cdot n_iw_{i}(x)f(x)\;\mathrm{d}\mu(x)\\ &=\sum_{i=1}^{n}\int_{\Omega}w_{i}(x)f(x)\;\mathrm{d}\mu(x)\\ &=\int_{\Omega}\sum_{i=1}^{n}w_{i}(x)f(x)\;\mathrm{d}\mu(x)\\ &=\int_{\Omega}\left(\sum_{i=1}^{n}w_{i}(x)\right)f(x)\;\mathrm{d}\mu(x)\\ &=\int_{\Omega}f(x)\;\mathrm{d}\mu(x)\\ \end{aligned} \]

  • 使用上面的这种方式就可以结合不同的采样策略（不同的采样 pdf）

确定 \(w_i\)

  • 如何确定 \(w_i\)
  • Balance heuristic
    • You can’t do much better than that, i.e. it’s always within a bound of the best strategy
    • Veach
    • \(c_i\) 表示使用第 \(i\) 种采样策略的概率
      • \(\sum_{i=1}^{n}c_i=1\)

\[ w_i(x)=\dfrac{c_ip_i(x)}{\sum_{k=1}^{n}c_kp_k(x)} \]

  • Power heuristic
    • better if there is one strategy with very low variance

\[ w_i(x)=\dfrac{p_i^{\beta}(x)}{\sum_{k=1}^{n}p_k^{\beta}(x)} \]

Balance heuristic

  • 细节推导

\[ \begin{aligned} E[F] &=\sum_{i=1}^{n}\dfrac{1}{n_i}E[F_i]\\ &=\sum_{i=1}^{n}\dfrac{1}{n_i}E\left[\sum_{j=1}^{n_i}\dfrac{f(X_{i,j})w_i(X_{i,j})}{p_i(X_{i,j})}\right]\\ &=\sum_{i=1}^{n}\dfrac{1}{n_i}\sum_{j=1}^{n_i}E\left[\dfrac{f(X_{i,j})w_i(X_{i,j})}{p_i(X_{i,j})}\right]\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n_i}\dfrac{1}{n_i}E\left[\dfrac{f(X_{i,j})c_ip_i(X_{i,j})}{p_i(X_{i,j})\sum_{k=1}^{n}c_kp_k(X_{i,j})}\right]\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n_i}\dfrac{c_i}{n_i}E\left[\dfrac{f(X_{i,j})}{\sum_{k=1}^{n}c_kp_k(X_{i,j})}\right]\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n_i}\dfrac{1}{N}E\left[\dfrac{f(X_{i,j})}{\sum_{k=1}^{n}c_kp_k(X_{i,j})}\right]\\ &=\dfrac{1}{N}\sum_{i=1}^{n}\sum_{j=1}^{n_i}E\left[\dfrac{f(X_{i,j})}{\sum_{k=1}^{n}c_kp_k(X_{i,j})}\right]\\ &=\dfrac{1}{N}\sum_{i=1}^{N}E\left[\dfrac{f(X_{i})}{\sum_{k=1}^{n}c_kp_k(X_{i})}\right]\\ \end{aligned} \]

  • 使用 MC 的方式的话，相当于使用一个联合分布 \(\bar{p}(x)\) 进行采样

\[ \bar{p}(x)=\sum_{k=1}^{n}c_kp_k(x) \]

  • 这样我们就可以很容易的将 BSDF 采样和对光源采样结合在一起
  • 一般而言，很容易实现对多种 pdf 的采样

效果图

效果图

法向半球采样

  • 19s

BRDF

  • 18s

Light

  • 8s

MIS with BRDF and Light

  • 12s

NEE

实现1

  • 37s

  • 1000spp, 417s

  • 可以看出来确实亮一些，是有偏的

实现2