GAMES103.王华民.10.Surface Waves

Posted on In Views:
流体模拟、表面波模拟、Shallow Wave Equation、细节处理（边界处理、two-way coupling）

流体模拟

  • Waves: An introduction to fluid simulation
  • 流体呈现的形态是各种各样的，因此很难有一个通用的模拟算法能够很有效率的、很好的模拟各种效果
    • 水、烟雾等

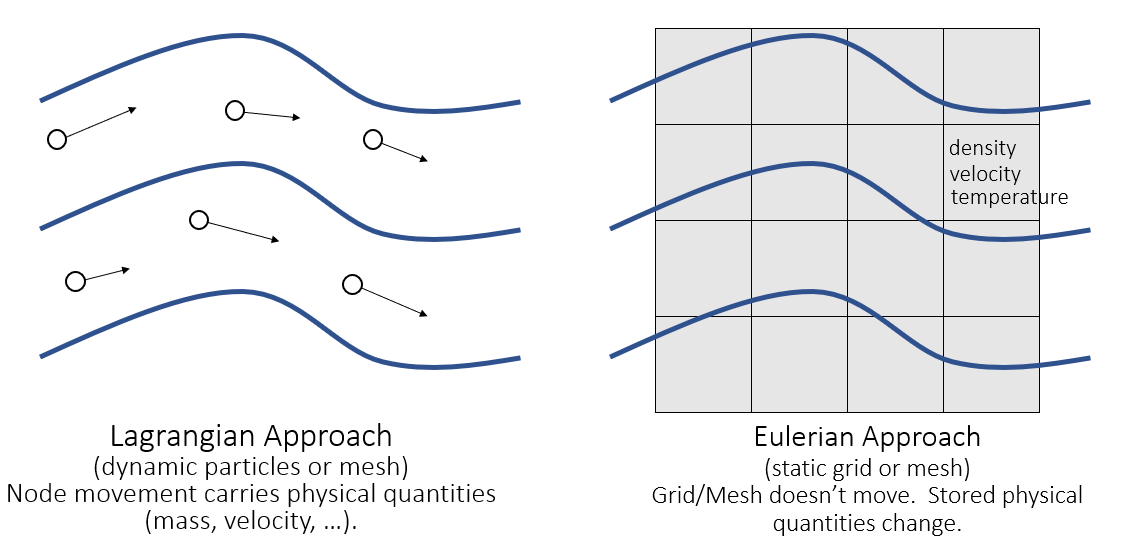
两种视角

  • 拉格朗日视角
    • 物理变量是定义在随物体运动而运动的一些物质点上的
    • 之前做的刚体、弹性体的模拟可以认为是拉格朗日视角的
  • 欧拉视角
    • 物理变量定义在空间网格中（不随物体运动而运动）

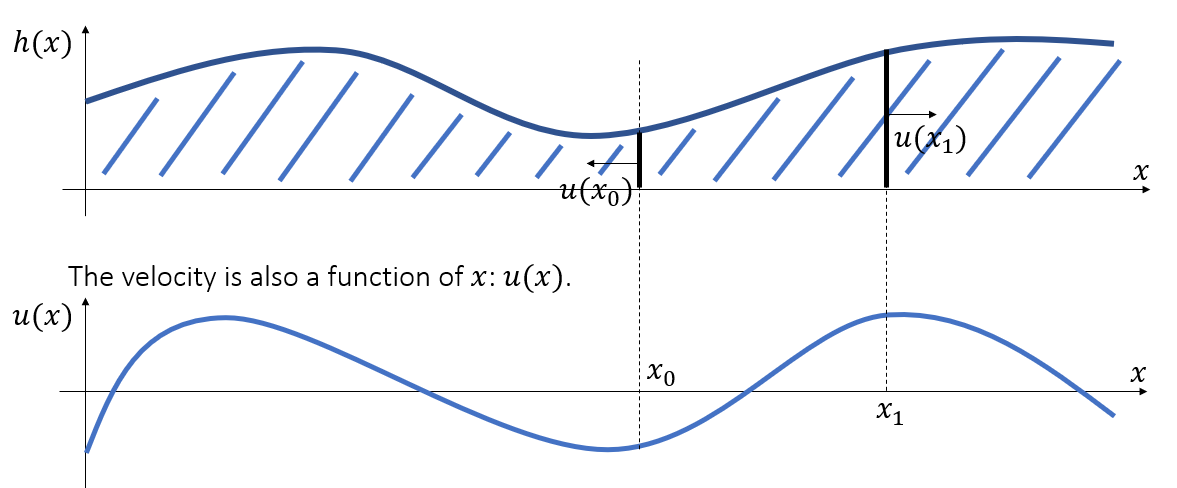
高度场

  • 高度场 \(h(x)\)
    • 定义每一个点的高度值
  • 2D 中，一般认为高度场是 1.5D 的
    • 因为高度场只能够表达函数能够表示的形式，是受限制的
    • 不能表示非函数形式，例如一个 \(x\) 对应多个 \(y\) 值
  • 速度（场）
    • 带方向，决定流体的流向

Shallow Wave Equation

  • 论文：Kass and Miller. 1990. Rapid, Stable Fluid Dynamics for Computer Graphics. Computer Graphics.

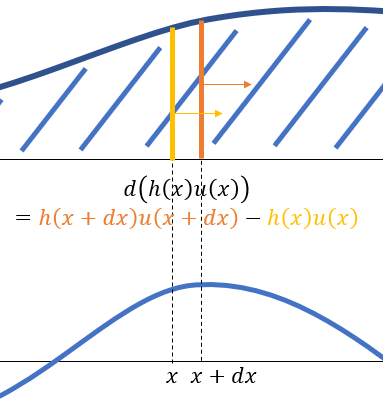
高度场更新

\[ \dfrac{\mathrm{d}h(x)}{\mathrm{d}t}+\dfrac{\mathrm{d}(h(x)u(x))}{\mathrm{d}x}=0 \]

  • 从微分的定义去理解
    • 体积的减小等于这一个点向外输送的流体体积

\[ \begin{aligned} &-\Big(h(x+\mathrm{d}x)u(x+\mathrm{d}x)\cdot\mathrm{d}t-h(x)u(x)\cdot\mathrm{d}t\Big)\\ =&(h(x+\mathrm{d}x)-h(x))\cdot\mathrm{d}x\\ \Longrightarrow&-\mathrm{d}(h(x)u(x))\cdot\mathrm{d}t=\mathrm{d}h(x)\cdot\mathrm{d}x\\ \end{aligned} \]

速度场更新

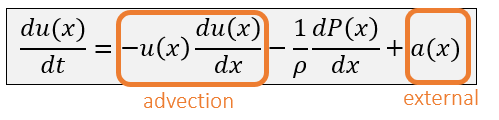
  • 由好几个部分构成
    • advection：水流的速度会随着自身的运动被带走
      • 想象某一个粒子，他的位置会随水流变化
        • 上一时刻 \(x\) 的速度，直接计算得到的并不是这一时刻 \(x\) 的速度（位置变了）
    • external：外力
      • 例如螺旋桨
    • 这里主要分析的部分
  • 不考虑 advection、external，我们得到如下的简化式子

\[ \dfrac{\mathrm{d}u(x)}{\mathrm{d}t}=-\dfrac{1}{\rho}\dfrac{\mathrm{d}P(x)}{\mathrm{d}x} \]

  • 物理量
    • \(\rho\)：密度
    • \(P(x)\)：压强
  • 直观理解
    • \(P(x+\mathrm{d}x)\) 大，则这个点的速度 \(u(x)\) 减小 \(\to\) 需要加一个负号
    • \(\rho\) 越大，越难推动
    • 量纲

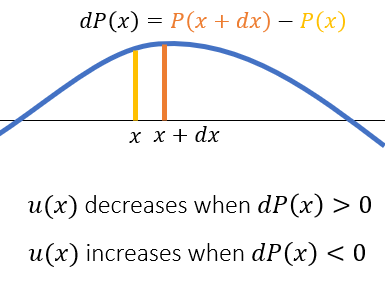
  • 具体物理推导：牛顿第二定律
    • 二维的，可以认为 \(\mathrm{d}V=h(x)\mathrm{d}x\)

\[ P(x+\mathrm{d}x)=\rho gh(x+\mathrm{d}x) \]

\[ \begin{aligned} \dfrac{\mathrm{d}u(x)}{\mathrm{d}t}&=a(x)\\ &=-\dfrac{(\rho gh(x+\mathrm{d}x)-\rho gh(x))\cdot h(x)}{\rho h(x)\mathrm{d}x}\\ &=-\dfrac{\mathrm{d}P(x)}{\rho \mathrm{d}x}\\ \end{aligned} \]

Shallow Wave Equation

  • 根据两个公式进行更新

\[ \begin{array}{c} \dfrac{\mathrm{d}h(x)}{\mathrm{d}t}+\dfrac{\mathrm{d}(h(x)u(x))}{\mathrm{d}x}=0\\ \dfrac{\mathrm{d}u(x)}{\mathrm{d}t}=-\dfrac{1}{\rho}\dfrac{\mathrm{d}P(x)} {\mathrm{d}x} \end{array} \]

  • Shallow Wave Equation
    • 假设波很小，产生的都是小水波 \(\Rightarrow\dfrac{\mathrm{d}h}{\mathrm{d}x}\approx0\)
    • 忽略高阶小项 \(\dfrac{\mathrm{d}h}{\mathrm{d}t}\cdot\dfrac{\mathrm{d}u}{\mathrm{d}x}\)
  • 链式法则展开

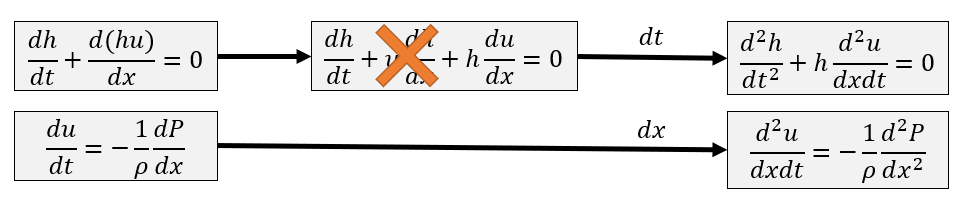
  • 合并得到 Shallow Wave Equation
    • 好处是不用管速度场了

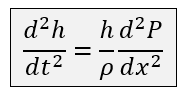
  • 此时问题转变成了对上述方程的离散化求解

离散化

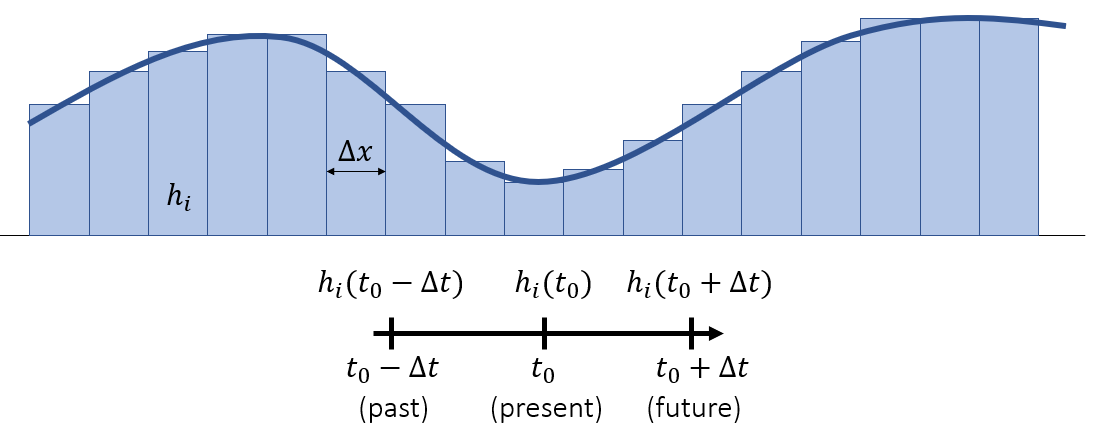
  • 如何将上面的微分算子和离散化之后的高度对应起来？

有限差分

一阶导数

  • finite differencing
  • 一阶近似：前向差分、后向差分

  • 二阶近似：中心差分

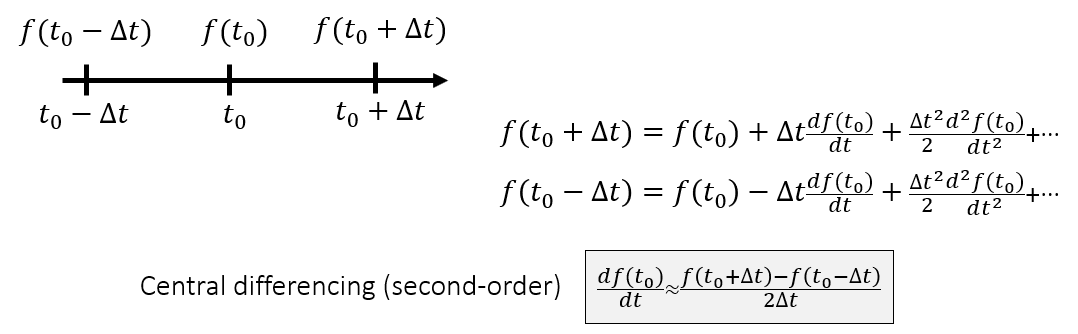
二阶导数

  • 先计算出来一阶导数，然后再计算二阶导数

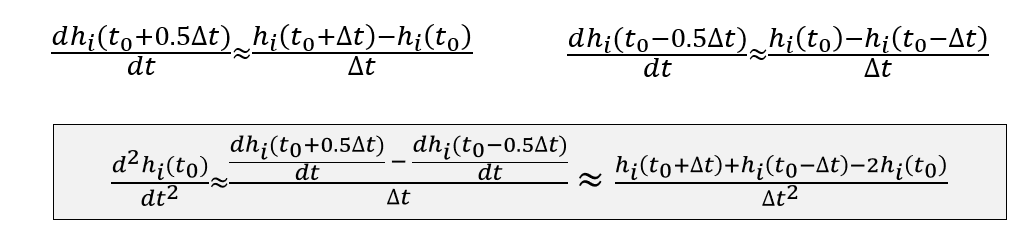
  • 一维拉普拉斯算子：\([1,-2,1]\)
  • 类似的可以计算：\(\dfrac{\mathrm{d}^2P(x)}{\mathrm{d}x^2}\)

离散化的 SW 方程

  • 得到了一个离散化之后的 \(h(x)\) 的更新函数

Volume Preservation

  • 保持水的体积不变（算法问题会导致体积变化）
  • 保持水的体积不变：\(\sum_{i}h_i(t)=\sum_{i}h_i(t-\Delta t)\)
  • 算法问题：黄色部分不能保证为零

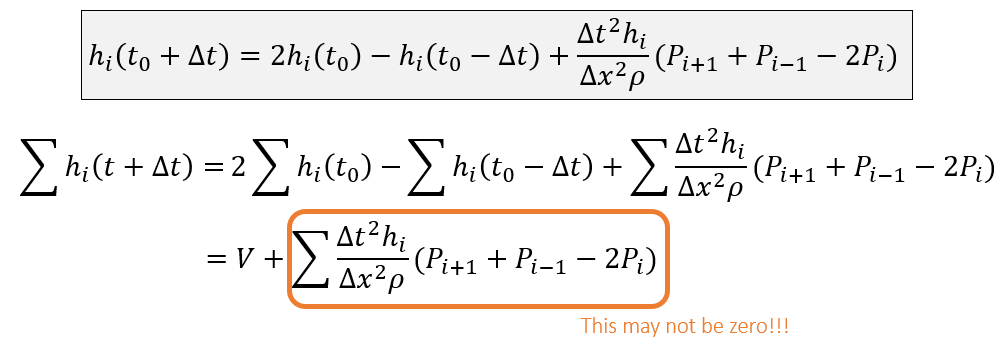
solution1

  • 直观理解：\(h_{i}\) 和 \(h_{i+1}\) 的交换量相同

solution2

  • 使用常数替代 \(h_i\)

压强

\[ P_i=\rho gh_i \]

  • 替换 \(p_i\)

Viscosity

  • 流体中的阻尼：粘滞
  • 类似于阻尼控制动量的变化 \(v_i(t_0)-v_i(t_0-\Delta t)\)

整体算法

其他细节

边界处理

  • Dirichlet boundary
    • 模拟范围外的高度都为一个常数（空气墙）
    • 一般用于模拟开放的水面（很大的海面）
  • Neumann boundary
    • 边界上的一阶导数为 0，边界没有流体交换（实体墙）
      • 无限高的边界，水出不来
    • 一般用于模拟小的水面

neumann boundary 算法

3D

Two-Way Coupling

  • 如何处理流体和其他物体的交互？
    • 流体与刚体、流体与气泡
  • Two-Way Coupling：影响是相互的
    • 液体对小方块有浮力
    • 小方块会把水排出去

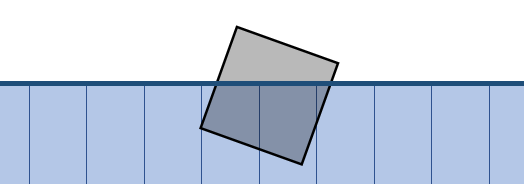
方块对流体

  • 关键问题：计算排水

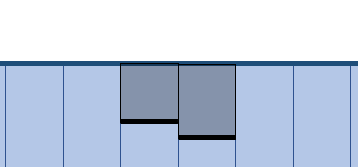
  • 如何排水？
    • 直接加到周围邻居的格子（当小方块占据空间很大时，不容易计算周围格子）
    • 添加虚拟高度（因为我们就是利用高度查进行水面模拟的）

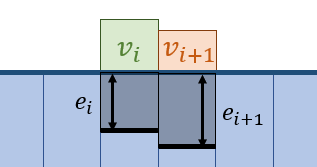
  • 虚拟高度如何确定？如何计算虚拟高度使其排出定量的水？
    • \(h_i^{\text{real_new}}=h_i-e_i\)
    • \(e_i\)：排水的高度（灰色部分）
    • \(v_i\)：增加的虚拟高度（绿色部分）
    • \(h_i^{new}\)：不添加虚拟高度模拟得到的结果

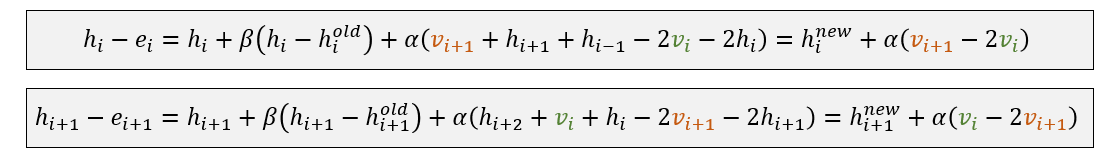
  • 求解 \(v_i,v_{i+1}\)

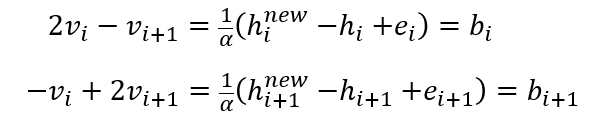
  • 我们允许拖动小方块，因此需要排水的位置 \(i\) 会变化，使用如下统一形式描述

  • 设置需要排水的位置的 \(b_i\)，添加需要排水位置的 mask/tag
  • 作业中使用共轭梯度法（PCG_Solver）求解
  • 算法

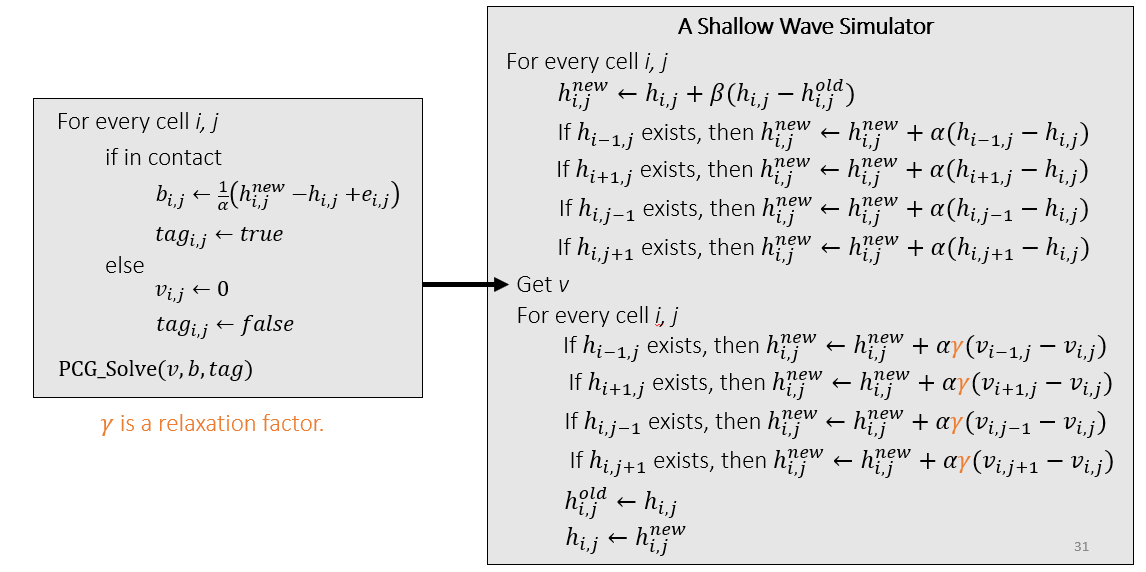
  • 添加一个系数 \(\gamma\)
    • 当我们快速拖动小方块的时候，会发现水浪特别大
    • 因为我们使用显示积分的方式计算，具有不稳定性
    • 添加系数不是物理正确的，但是能够让模拟看上去稳定

流体对方块

  • 阿基米德定律：\(F_{浮力}=\rho gV_{排}\)

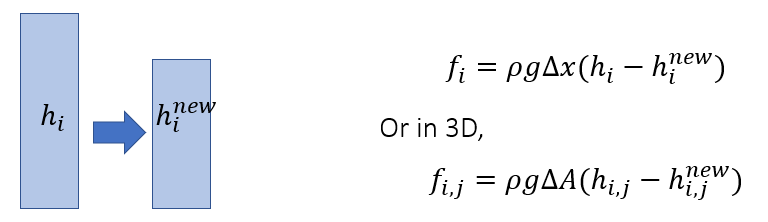
  • 需要考虑不同小格子对小方块的力，考虑这些力对方块的作用
    • 移动、旋转（力矩）
  • 旋转的准确模拟可能需要使用隐式积分的方式
    • 高度场的隐式积分是可以做的