(论文)[2021] A Survey on Bounding Volume Hierarchies for Ray Tracing(4)

Posted on Edited on Views:
关于层次包围盒的一篇 survey（拓扑结构优化，在建立好一颗 BVH 之后如何做优化，结构旋转，删除与插入，PRBVH，TRBVH）

BVH Survey

4. construct bvh

4.5. Topology Optimization

  • 我们在构建 BVH 的过程中，无法知道子结点的代价函数值，因此都是做的局部优化（简化）
    • 例如将子节点的内部节点都当作叶子节点来考虑
  • 因此结构优化就是先建立好一个 BVH，然后对其进调整优化
  • 这一部分的优化目标基于 SAH（内部节点的 BVH 表面积之和最小）

tree rotation

  • 树结点的旋转操作（二分查找树的旋转操作）
  • 一共有 4 种旋转方式
  • 论文提出了两种方法
    • Hill Climbing
    • Simulated Annealing：避免陷入局部极值

Hill Climbing

  • 按照中序遍历的方式一次检测每一个节点
    • 对每一个节点做如下操作
    • 计算当前点的代价函数
    • 应用上面的 4 种旋转（不行则不旋转），记录代价函数减小最多的旋转
      • 如果有减小，使用这个旋转更新，同时更新当前点的代价函数值
      • 如果没有减小，则检测下一个节点
  • 问题：可能会陷入局部极值（很多情况下）

Simulated Annealing

  • 模拟退火
  • 基本思想是，对于可能增加 SAH 的旋转，也有一定概率接受（可能会走向全局最优）

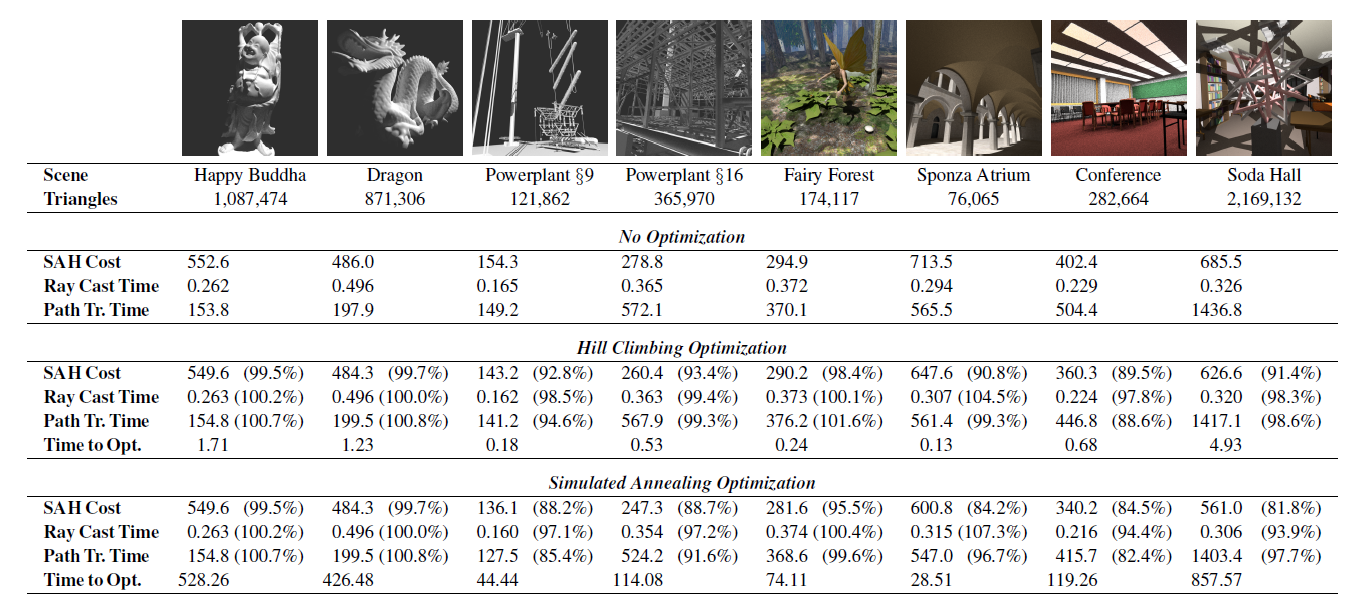
结果

remove and reinsert

  • Fast Insertion-Based Optimization of Bounding Volume Hierarchies.
    • 移除一棵子树，然后把这棵子树中的节点重新插入
    • 查找空间很大，因此需要确定处理子树的顺序
      • 一个直观的顺序：按照 SAH 的代价函数值的大小（下图）
    • 查找新位置
      • 带剪枝的搜索算法（分支限界算法）

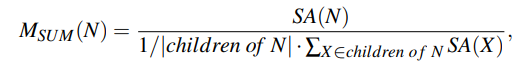
  • T-SAH: Animation Optimized Bounding Volume Hierarchies
    • 使用 Metropolis-Hastings sampling 的方式优化先移除哪一棵子树

PRBVH

  • 一个很重要的假设：每个叶子节点只包含一个三角形
  • 论文：Parallel Reinsertion for Bounding Volume Hierarchy Optimization
  • 并行化，把上面的问题重新形式化成一个可以并行的问题
    • 最终结果：类似质量下，比原来串行化快两个数量级
  • The key insight：我们在计算 SA 缩减的时候不需要真正去移除子树，找到最优位置之后再进行移除
  • 给很多个 node 并行的找最优的插入位置（SAH cost 减少最多）
  • 思路：迭代算法
    • 输入为一个任意的 BVH，然后迭代优化，每一轮迭代并行执行一组 reinsertion 操作
    • each node searches for its best output node in parallel
    • the conflicts between nodes are resolved using the locking scheme
    • The nodes with successful locks can be reinserted
    • After the reinsertion, we recompute the bounding boxes and the SAH cost
  • SAH cost

\[ c(N)=\dfrac{1}{SA(N)}\left[c_T\sum_{N_i}SA(N_i)+c_I\sum_{N_l}SA(N_l)\vert{N_l}\vert\right] \]

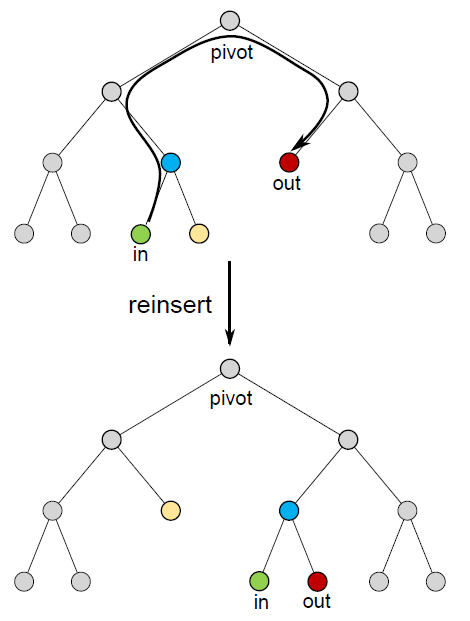
Reinsertion Operation

  • 对每一个节点
  • 将其所在的子树（绿色）连同它的父节点（蓝色）一起移除，然后将其兄弟节点（淡黄色）放到父节点原来的位置
  • 将移除部分插入到找到的最优位置（红色），将这个位置原来的节点挂在兄弟节点的位置

  • 每一个叶子节点都只包含一个三角形
  • 此时优化 SAH cost，就等价于优化这个部分（其他都变为常数）

\[ \sum_{N_i}SA(N_i) \]

  • 形式化优化问题：maximization of the surface area decrease
    • 等价于最大化受影响的 BVH 的 SA 减小
  • 受影响的 BVH 只有输入、输出节点之间的路径
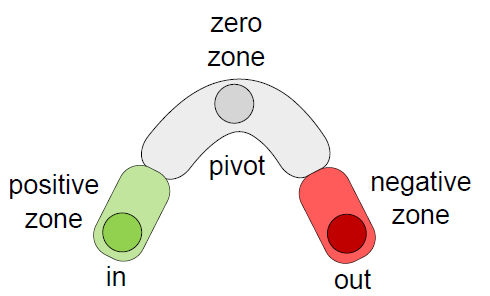
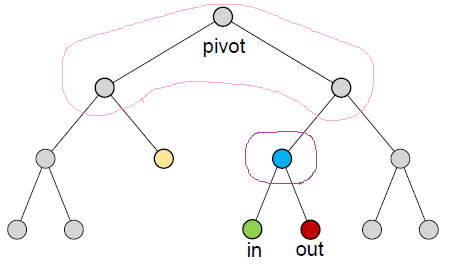
    • 上图中的 in-pivot-out
    • pivot：最近公共祖先节点
    • 移除：\((pivot,in]\) 中的节点的 SA 的减小的非负的（一定减小或不变）
    • 插入：\((pivot,out]\) 中的节点的 SA 的减小是非正的（一定增加或不变）
  • 可以按照 SA 是增加还是减小，将这些路径上的节点划分为几类
    • 路径不包括 in 节点、in 节点的父节点、output 节点

  • 对一个输入节点 in，如何寻找输出节点 out？
    • 查找所有树上的节点（除了以 in 节点为根的子树内的节点）
    • 利用 parent 指针可以不使用辅助的栈结构实现
      • 利用一个 bool 记录是上行还是下行，利用指针进行上下游走
      • python 代码
  • 总的来说就是一个带剪枝的找最优 output 位置的算法
  • 对于所有的节点，可以并行地找出最佳位置
算法细节
  • demo
  • 初始化的最优 out 节点就是 in 节点的兄弟节点
    • decrease=0
  • \(d_{bound}\)：整条路径的 SA 减小的上界
    • 就是对 \(d_{direct}\) 上界的估计
  • \(\mathbf{b}_{pivot}\)：去掉 in 节点之后的 pivot 的包围盒
    • \(\mathbf{b}_{pivot}\) 的计算：pivot 的右子节点的包围盒和 \(\mathbf{b}_{pivot}\) 的并集
    • 用于累计计算路径上 SA 的减小
  • 有些在算法运行过程中不变的量
    • \(\mathbf{b}_{parent},d_{bound}\)
  • 整体是一个前序遍历的算法
  • \(d\) 是进入到新的节点之后才被更新

down=True

  • down=True

  • \(d\)：搜索到当前 out 节点为止，路径上的 SA 减少值

    • 粉红色路径的 SA 减小值
    • 这里的更新是更新粉红色路径最后的节点的 SA，相当于在原来的子树内插入了 in 节点
      • 减少值就是 \(SA(\mathbf{b}_{out})-SA(\mathbf{b}_{merge})\)

  • \(d_{direct}\)：紫色路径（蓝色节点）的 SA 减小值（原来是 in 的父节点）

    • 因此这里的更新使用 \(SA(\mathbf{b}_{parent})-SA(\mathbf{b}_{merge})\)

  • 剪枝：由于 \(d\) 在 down=True 的遍历过程中是不增的

    • \(d_{max}\le d\)（\(d\) 表示当前计算得到的 \(d\)）

    \[ \begin{aligned} d_{may\_be\_best} &=d_{max}+d_{direct}\\ &\le d+d_{direct}\\ &= d+SA(\mathbf{b}_{parent})-SA(\mathbf{b}_{merged})\\ &\le d+d_{bound} \end{aligned} \]

  • down 的更新

    • 剪枝向上回溯
    • 如果没有左子节点，则向上回溯

down=False
  • 首先更新 \(d\)：去除最后一个结点的减小值
  • 两种情况分类讨论：子树的前序遍历完成、还处于前序遍历的 up-phase
  • 遍历完成
    • 更新 pivot 的包围盒值
      • 原来的 pivot 的包围盒记录的是 pivot 左子树的包围盒
        • 因为 in 插入到 pivot 子树中时，pivot 的 SA 变化为 0，不影响 \(d\) 的计算
      • 不包含 in 节点
    • 27-29：out=pivot
    • 33-36：in 节点不能插入到父节点位置，除了父节点，都需要进行尝试
    • 更新 \(d\)：pivot 减去 in 节点 SA 减小了多少
    • 42-44：对兄弟子树进行遍历
  • up-phase
    • 从左子节点上来，则继续遍历右子节点
    • 从右子节点上来，则继续向上

Parallel Reinsertion

  • 解决可能存在的冲突问题
  • 两种冲突
    • topological conflicts
    • path conflicts

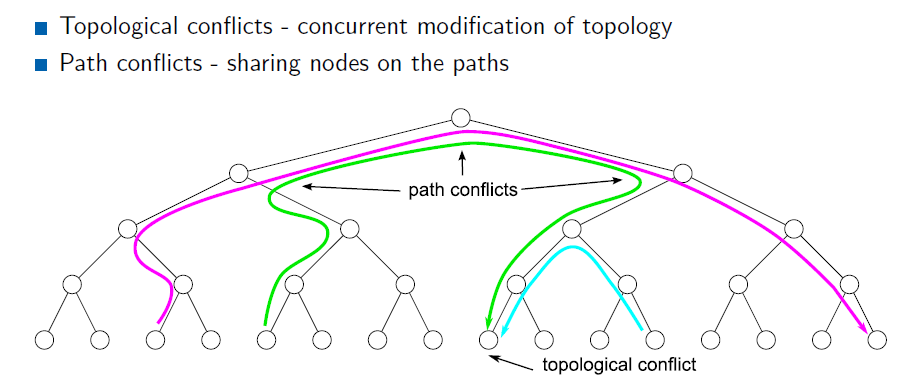
  • 当发生冲突的时候，丢弃优先级小的
  • topological conflicts：同时修改树结构
    • 并发操作加锁，SA 减小更多的优先操作
    • 锁定影响到的节点
  • path conflicts：同时修改 BVH
    • 锁定路径上的所有节点
Locking Strategy
  • 保守的：path+topological 都加锁
    • 一定能够保证 SA 减少的总量和所有成功加锁的 path 的 SA 减少之和相等
  • 激进的：topological 加锁
    • 不能保证总量和分量之和想的相等（可能多、少、相等）
    • 实验表明，收敛更快
激进策略分析
  • 对于一个 AABB 包围盒来说，决定这个包围盒的内部包围盒最多只有 6 个（一个面一个）
    • 如果有两个包围盒决定了同一个面，选择一个即可
移除
  • 不同节点的内部节点移除
    • 只有决定了包围盒的面的节点移除才会有 positive SA decrease
    • 如果和其它节点共同决定一个面，那么移除这个节点对这个面，SA 无变化
    • 不决定面，则 SA 无变化
  • 同时对有 positive SA decrease 的节点进行移除，可能会导致总的减少比部分减少之和要小
    • 例如移除决定相邻的面的两个节点
      • 下图中的 1、2、3，虚线方框部分的在总的减少中只会被计算一次
  • 同时移除也可能导致总的减少比部分减少要大
    • 决定面的节点的移除，使得本身不决定 bvh 面的节点决定面
      • 下图中的 4、5，本身不决定 bvh 面的节点变成决定面

插入
  • 插入的时候也有类似的问题，本身所有的节点插入，都会有 negative SA decrease
  • 总的增加 < 分量增加之和
    • 1、2、3：图 3 的右下角虚线黑框只会被总的计算一次
    • 5：内部有些红色节点的插入本身会导致 SA 增加，但是现在不会了
  • 总的增加 > 分量增加之和
    • 3、4：一开始最左边红色块的插入不需要计算图 4 的两个黑色虚线黑框内的部分

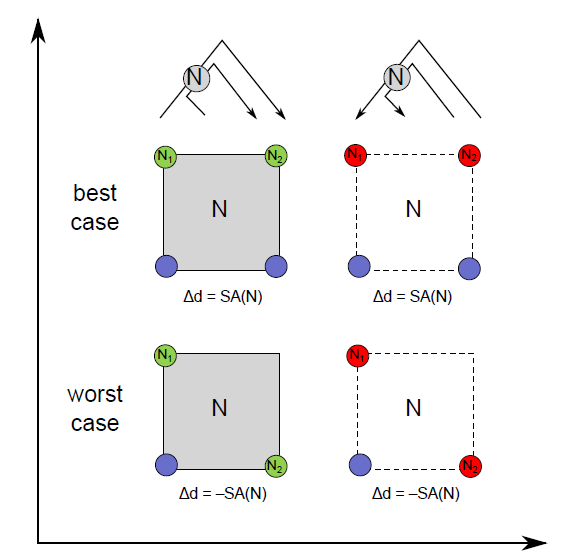
最好最坏情况分析
  • two path analysis
  • 移除（下图中的绿色节点移除）
    • 最好：单个移除不影响 bvh，两个一起移除 SA \(\to\) 0
    • 最差：单个移除 SA \(\to\) 0
  • 插入（下图中的红色节点插入）
    • 最好：单个插入 SA 的增加和两个插入一样
    • 最差：单个插入 SA 的增加都为 0，但是两个插入让其变大
      • 红色为点（退化的 bvh）

  • 为什么激进策略更好呢？
    • 锁住的节点少，在一次迭代能够有更多操作同时进行（throughput）
    • 一开始的时候，positive SA decrease 比 negative SA decrease 更多，因此总的效果来说是更好的
    • 大量移除的节点都是不决定原来的 bvh 的
      • 可能会有更多的 SA decrease，在移除其他节点之后决定了 bvh
    • 大量插入的节点都是不决定最终的 bvh 的（不会导致 SA increase）

完整算法

  • sparse search
    • 算法瓶颈是在查找 search phase
    • 相邻的节点搜索得到的路径引起冲突的可能性比较大，因此同一轮的搜索中，相邻的几个节点我们尽量只搜索少量几个
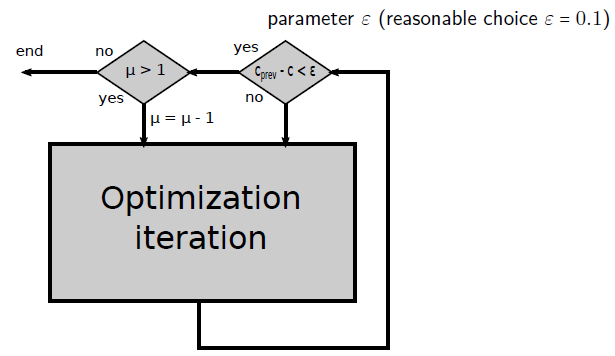
    • 只有满足如下式子的 \(i\) 才进行搜索，\(I\) 表示迭代轮数，\(\mu\in\{4,\cdots,9\}\)

\[ I(\mod\mu)\equiv i(\mod\mu) \]

  • 终止条件
    • 两次迭代的 SA cost 差异小于 \(\epsilon\)
    • 实验值：\(\epsilon=0.1\)
  • GPU 实现
    • Find the best node
    • Lock nodes
    • Check locks
    • Reinsert
    • Recompute bounding boxes
    • Compute the SAH cost

TRBVH

  • treelet restructuring
    • treelet：small subtrees of a fixed size
  • 基本思想是重构树形结构
    • 每次使用动态规划的方式重构一个 treelet
    • bottom-up
  • 改进
    • 使用 agglomerative clustering（聚集方法）代替动态规划，能够处理更大的 treelet