(论文)[2021] A Survey on Bounding Volume Hierarchies for Ray Tracing(3)

Posted on Edited on Views:
关于层次包围盒的一篇 survey（BVH 的构建、增量更新、LBVH 的构建）

BVH Survey

4. construct bvh

4.3. Incremental Construction

  • 论文：Automatic Creation of Object Hierarchies for Ray Tracing
  • 在插入的时候增量更新
  • 初始的时候为一个人空的 BVH，当插入新物体的时候，找到一个合适的叶子节点进行插入，如果插入之后节点过大则进行分裂
  • 在初始的时候不知道场景中所有物体的时候很有用
    • e.g., streaming the data through the network
  • 质量通常不是很高
  • 在另一篇论文中改进了
    • Incremental BVH Construction for Ray Tracing
      • 以优先队列的方式选择插入场景中的原体，同时贪心的最小化每次插入的代价，结合下面这篇论文的方法，防止插入的时候达到局部最小化
    • Fast Insertion-Based Optimization of Bounding Volume Hierarchies

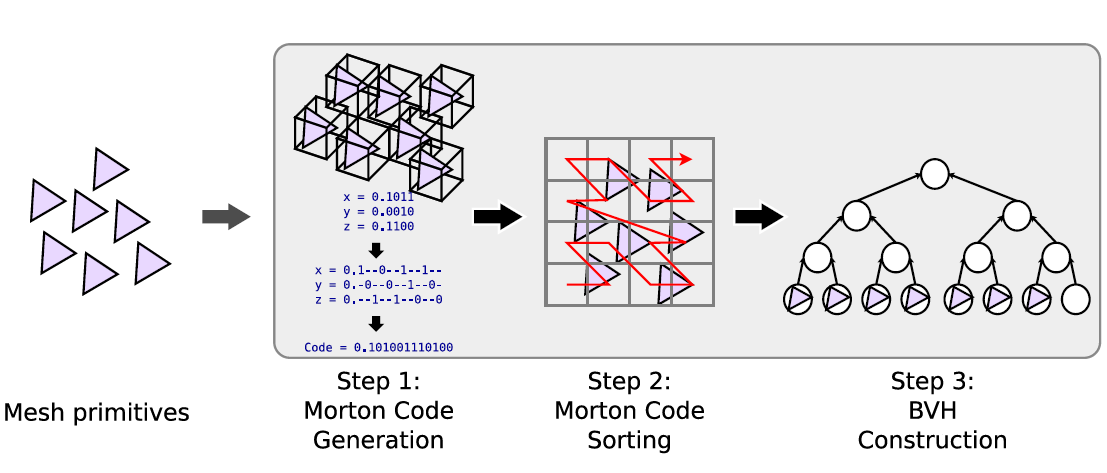
4.4 LBVH

  • BVH 构建上的并行不是很直观
  • 归约：BVH 的构建能够被归约为对场景原体在 Morton Curve 上的排序，顺序由定长（32/64bit）的 Morton codes 决定
    • 排序则有很多并行算法
    • 定长：可以使用基数排序的方式 \(O(n)\) 实现
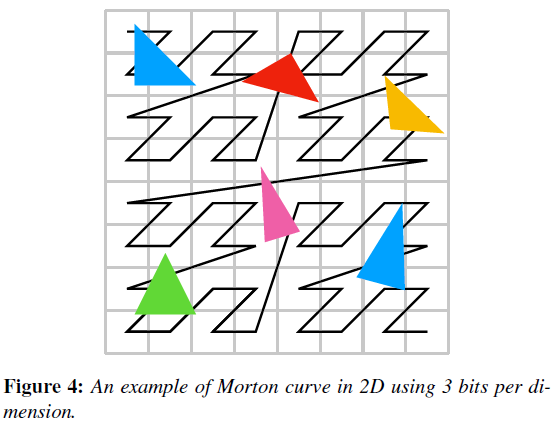
  • Morton curve：space-filling curve subdividing space into a uniform grid
    • 每一个小的 grid 都会被分配一个唯一的 morton 码（容易计算）

LBVH

  • linear BVH (LBVH)
    • 使用 Morton Curve 构建 BVH，GPU-based
    • top-down
    • 每一个 level 调用一次 kernel
    • lower level 的时候使用 SAH binning 算法
  • 论文：Fast BVH Construction on GPUs
  • 算法整体思路
    • linearizing：将输入的原体转化为一个长度为 \(n\) 的定长序列
    • 然后我们对所有区间进行递归划分，从而构建起 BVH，每一个节点都对应一段区间
      • root：\([0,n)\)
    • 每一个 BVH 上的几点就对应 \([l_i.r_i)\) 内的原体
  • Morton curve：space filling curve
    • 又被称为 Lebesgue curve / z-order curve
  • 假设
    • 使用 AABB 包围盒
    • 每个原体的包围盒都是已知的
    • 整个场景的包围盒是已知的
  • 使用每个原体的重心表示这个原体
  • 将整个场景的包围盒划分为 \(2^k\times2^k\times2^k\) 个格子，于是每一个格子能够使用 3 个 k bit 的整数来表示
  • morton code 例子如下图所示
    • 拼接，然后构成一个顺序

  • 然后根据每一个原体重心的位置为其分配一个 Morton code，根据这个码进行排序
  • 按照 Morton code 进行排序得到的结果，能够让相邻的原体在空间位置上也是相邻的
  • 一个例子

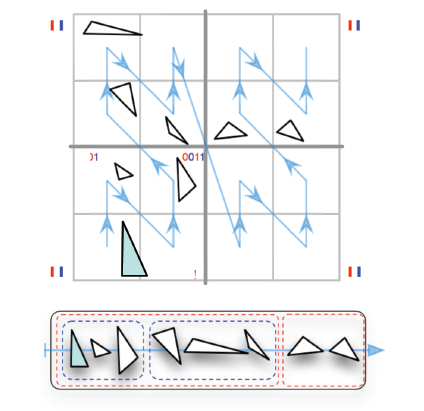
  • 构建 BVH
    • 从最高位开始，将为 0/1 的原体分别划分到两棵子树内
      • 如果全部相同，则看下一位
    • 递归处理子树，直到所有位都处理完毕
  • 构造过程等价于 MSD 的 2-基数排序（most-significant-bit radix-2 sort）
    • 泛化到 most-significant-bit radix-\(2^b\) sort（每次比较 \(2^b\) 位），则可以构造出 \(2^b\) 叉树
    • radix-8：octree
  • 并行算法
    • 先排序（并行算法），然后从排好序的序列中构建出 BVH
  • 排序
    • 排序过程中由于高位可能全 0，使用 LSD 效果更好

构建

  • 每一个 morton code 都表示了一个从根节点到这个原体的唯一路径，他们的包围盒就是最近的公共祖先节点
    • 例如：0000,0001,0011 \(\Longrightarrow\) 00
  • 对每一组相邻的原体 \((i,i+1)\) 做如下处理
    • 如果这两个原体，从高位到低数，第 \(h\) 位开始不一样，则它们在第 \(h,h+1,\cdots,3k\) 层将被隔开（处于不同的 BVH）节点中，因此我们记录如下的 pair

\[ \Big[(i,h),(i,h+1),\cdots,(i,3k)\Big] \]

  • 我们将所有的 pair 合在一起，并将它们按照第二个关键字排序，则得到了在某一层的分裂信息
  • 根据这个分裂信息，进行构建
  • 勾结按结果可能存在只有一个儿子的父节点，需要收缩，对每个子结点都向上收缩一遍路径

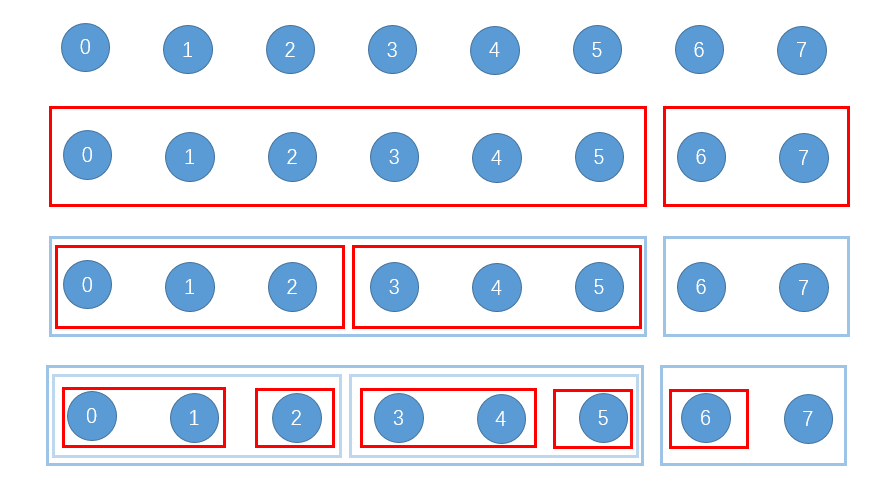
构建例子

  • 所有的 Morton code 如下
1
2
3
4
5
6
7
8
0: 0000
1: 0001
2: 0011
3: 0100
4: 0101
5: 0111
6: 1100
7: 1110
  • 得到的的 pair 如下
1
2
3
4
5
6
7
(0, 4)
(1, 3), (1, 4)
(2, 2), (2, 3), (2, 4)
(3, 4)
(4, 3), (4, 4)
(5, 1), (5, 2), (5, 3), (5, 4)
(6, 3), (6, 4)
  • 排序
1
2
3
4
(5, 1)
(2, 2), (5, 2)
(1, 3), (2, 3), (4, 3), (5, 3), (6, 3)
(0, 4), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4)
  • 构建顺序的示意图如下
    • 最后一行划分为单原体的包围盒没有画出来

HLBVH

  • hierarchical LBVH
    • combine LBVH with SAH sweeping for the upper levels
  • 将 sweeping 改进为使用 binning
    • 使用 morton code 的前缀作为 bin 的下标
    • 引入和很多同步（并行不友好）

加速构建1

  • 论文
    • Maximizing Parallelism in the Construction of BVHs, Octrees, and k-d Trees
  • 一次 kernel 的调用便构建好整棵 BVH
    • 之前 LBVH 的构建 level 与 level 之间有相互依赖，这里消除这个依赖
  • idea：内部节点和叶子节点放在两个数组里面
    • 内部节点的位置和属于该区间的某个端点原体相一致（分裂时的端点）

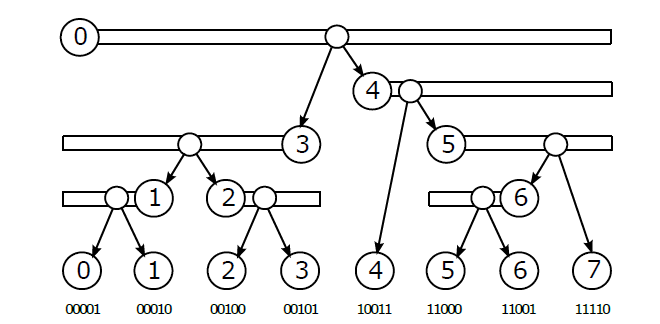
  • 加速从排好序的原体中构建出 BVH
    • 我们知道一定会有 \(n-1\) 个内部节点
  • \(I,L\)：内部节点、叶子节点
  • 根节点 \(I_0:[0,n-1]\)
    • 左子节点 \([0,\gamma]\)，右子节点 \([\gamma+1,n-1]\)
    • 如何确定 \(\gamma\) ？
  • \(\delta(i,j)\)：表示 \(k_i,k_j\) 的最长公共前缀的长度
    • 如果 \(j\notin[0,n-1]\) 等于 \(-1\)
  • 算法：确定节点 \(I_i\) 的左右端点（至少含有两个原体）
    • 其中一个端点是确定的，\(k_i\in I_i\)
      • 直观的理解，每一对相邻的节点只会被分裂一次，因此可以有这种规定
    • 确定方向，左还是右（那一边公共前缀的长度更长）
      • 不存在 \(a<b<c\) 的公共前缀长度相同（二进制表示），否则则有 \(\text{x1,x2,x3}\)（\(\text{x}\) 表示前缀）
    • \(I_i\) 内部的最长公共前缀一定要大于 \(\delta(k_i,k_{i-d})\)，否则不是分裂点
      • 根据这个性质去找另外一个端点
    • 找端点，找端点只是为了更新 \(\delta_{node}\) 的值
      • 6-8 行，先确定另外一个端点的最大返回
        • 倍增尝试
      • 10-14 行，找到端点之后，使用二分进行结果的查找
        • 原理：\(\delta(a,b)\ge\delta(a,c),a<b<c\)
    • 接下来确定分裂点（左右子节点）
      • 二分查找（分裂点左右两段内部的 \(\delta>\delta_{node}\)）
  • 结果图

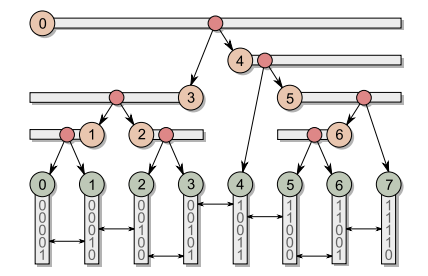
  • 伪代码如下

  • c++ 代码
  • 这里的问题是，这个 pass 只是构建好了 BVH 的拓扑结构，实际上 BVH 中 AABB 包围盒的计算并没有算出来
  • 计算 AABB 包围盒
    • 每一个叶子节点一个线程，从叶子节点出发向根节点移动计算 AABB 包围盒
    • 使用全局的原子计数，记录到达每一个内部节点的线程数，当下一个线程处理到这个节点时，前一个处理过这个节点的线程马上终止
    • 每一个节点只会被一个线程同时处理，时间复杂度是 \(O(n)\) 的，同步问题

加速构建2

  • 论文
    • Fast and Simple Agglomerative LBVH Construction
  • 在加速构建1的基础上进行优化
  • 一次 kernel 调用便同时构建好拓扑结构和 AABB 包围盒
    • 必须是 bottom-up fashion
  • 使用了另外一种分布方式

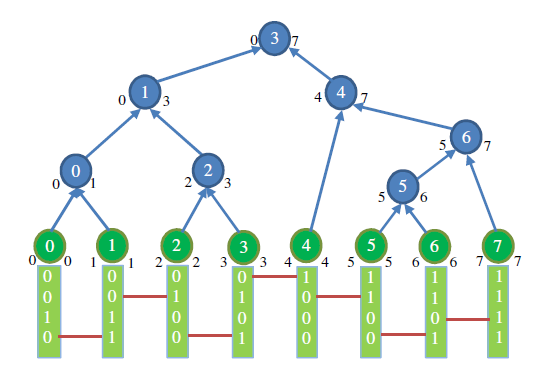
  • 如果某一个节点覆盖了范围 \([a,b]\) 之间的 keys，那么下标为 \(a-1,b\) 的两个节点都是当前节点的祖先节点，其中有一个为当前节点的父节点
  • 定义函数 \(\delta(i)\)，表示内部节点 \(i\) 覆盖的 keys 的最不同位的下标
    • 例如节点 \(i\) 包含的 keys 为 0010,0011,0100,0101，\(\delta(i)=2\)
    • 于是如果 x 节点是 y 节点的祖先节点的话，就有 \(\delta(x)>\delta(y)\)
      • 根据这个性质，我们可以判断 \(\delta(a-1),\delta(b)\) 的大小关系，来选择父节点
    • 实际实现可以使用两端点的 key 异或实现（偏序关系是一致的）
  • 如何计算 \(\delta(i)\) 
1
2
3
4
5
// delta function in sec3 of the paper
// "Fast and Simple Agglomerative LBVH Construction"
__forceinline uint32_t Delta(const std::vector<glm::uvec3> &leaves, const uint32_t id) {
    return leaves[id + 1].z ^ leaves[id].z;
}
  • 为什么可以这么做呢？
    • 上面的红线其实就表示了这两个节点在哪一层会被连接
    • \(i\) 号内部节点一定包含叶子节点 \(i\)
    • 因此这就成了判断：是 \(i\) 号节点会先被加进来合并还是 \(j\) 号节点会先被加进来合并
      • 同时一个内部节点必然包含至少两个 key
      • 上面的计算其实就是算出了红线的位置
  • 可以这么理解，内部节点 \(i\) 的子节点必然是 \([x,i),[i,y)\)
    • 这样就可以理解上面的计算了
      • 哪边差异小，哪边就会先被连接
    • 这么理解的话，内部节点的标号也就是肯定的了（不会有冲突），因为每一个相邻的位置只会被分裂一次
  • 构建包围盒的算法和加速构建1一致
  • 感觉这里的优化似乎是省掉了加速构建1中的拓扑结构生成部分，把拓扑结构生成直接集成到构建包围盒中

其他优化1

  • 内存优化，紧凑表示，无冗余表达（指针）
  • This algorithm is the fastest construction algorithm to date.
  • pipeline

  • ostensibly-implicit layout
    • 能够快速检测得到二叉树中的缺失部分，能让排布更紧凑
    • 只需要保存包围盒的信息，其他信息都能够推断出来（不需要保存）

ostensibly-implicit layout

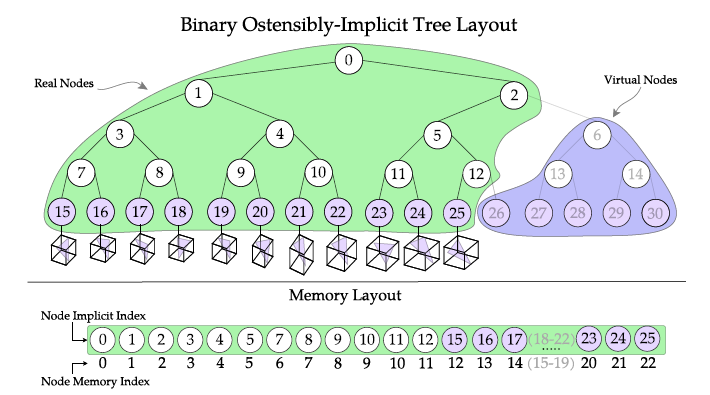
  • 数据结构
    • 完全二叉树：需要引入虚拟节点
    • 堆结构：需要预处理，需要存储指针数据
    • ostensibly-implicit layout：不需要存储指针（多余的数据），同时不需要预处理
  • idea：构造一棵隐式的完全二叉树，把虚拟节点都放在最右边，然后编码一系列的小的完全二叉树
  • 物体个数为 \(t\)
  • 最深的一层需要引入的虚拟节点的个数 \(L_v=2^{\lceil \log_2t\rceil}-t\)
  • 最深的一层总共的叶子结点数 \(L_c=t+L_v=2^{\lceil \log_2t\rceil}\)
  • 因此树上总结点数 \(N_c=2L_c-1\)
  • \(N_c=N_r+N_v\)
    • \(N_v\)：virtual node（树上的虚拟节点总数）
    • \(N_r\)：real node（树上真实的节点的总数）
  • \(L_v\) 可以表示成 2 的幂次方的和，定义如下集合
    • \(N\) 应该和二进制表示中 \(1\) 的个数相等

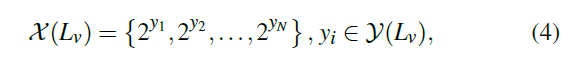
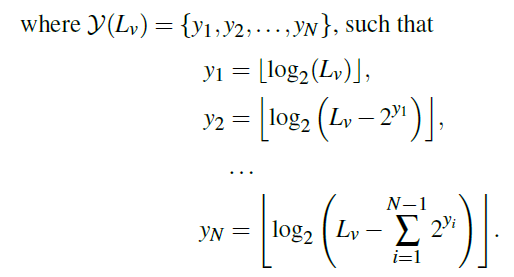
  • \(N_v\) 和 \(L_v\) 有如下关系
    • 叶子数为 \(x_k=2^{y_k}\) 构成的完全二叉树的总结点数为 \(2x_k-1\)
    • 参考上图中的紫色部分，从右往左
      • 4（27,28,29,30）向上形成一棵完全二叉树
      • 1（26）又向上形成一棵完全二叉树

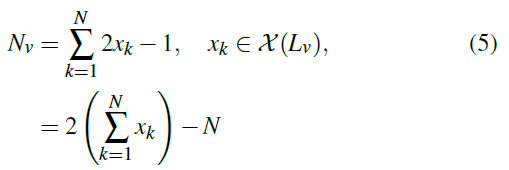
  • \(count\_set\underline\_bits(X)\) 表示计数 \(X\) 的二进制表示中 \(1\) 的个数
  • 上面的式子 (5) 表示如下

\[ N_v=2L_v-count\_set\_bits(L_v) \]

  • 更新

\[ \begin{aligned} N_r &=N_c-N_v\\ &=(2L_c-1)-(2L_v-count\_set\_bits(L_v))\\ &=2t-1-count\_set\_bits(L_v) \end{aligned} \]

建立映射

  • 一个真实的节点，假设它对应的虚拟节点下标为 \(i\)
  • 虚拟节点深度 \(l_i=\log_2(i+1)\)，\(0\le l_i\le \bar{l}=\lceil{\log_2t}\rceil\)
  • 位于深度 \(l\) 的虚拟节点个数如下

\[ L_{vl}=\left\lfloor{\dfrac{L_v}{2^{\bar{l}-l}}}\right\rfloor=L_v\gg(\bar{l}-l) \]

  • 因此这个节点在内存中的位置 \(i_m\)

  • \(N_{vl}\) 的计算如上面提到的一样

\[ N_{vl}=2L_{vl}-count\_set\_bits(L_{vl}) \]

建立 BVH 算法

  • 我们获取到的是按照 Morton code 排序之后的原体序列
  • 内部节点和叶子节点分开存储
    • 叶子节点的包围盒可以提前知道，之前已经算出来了
  • [3] tNode：上面提到的 \(j\)
    • 需要通过上面 \(eq(9)\) 的计算，得到真实的内存地址
  • [23,24] 为了同步，第一个到达当前结点的线程不操作（和之前的优化方法类似）

  • 一个别人代码的实现
  • 评价：质量可能不是很高，但是 BVH 构建很快，而且内存占用少（指针隐式表示）

其他优化2

  • 扩展了 Morton code，同时将场景中原体的大小编码进去了，能够提升 BVH 的质量