(论文)[2021] A Survey on Bounding Volume Hierarchies for Ray Tracing(2)

BVH Survey

• 目录

4. construct bvh

4.1 Top-Down Construction

• 借鉴 KD-tree 的建立过程
  • On Fast Construction of SAH-based Bounding Volume Hierarchies.
• 算法
  • 根节点包含场景中所有的原体
  • 从根节点开始，将包含的原体划分为两个不相交的子集（对应两个子节点）
  • 对子节点做递归的操作，直到遇到终止条件
• 终止条件
  • 节点中包含的最大原体数目（叶子节点）
  • 最大树深度
  • 最大使用内存
• 问题：划分为两个子集的方式很多，是指数级别的（NPC）
  • Object partitioning considered harmful: space subdivision for BVHs
    • AABB 包围盒 \(O(n^6)\) 的方法
    • 进一步可以利用 grid approximation 控制时间复杂度，同时受限于 grid 的分辨率，可能只是个局部最优
• BVH 中，每一个原体只会被引用一次
  • 引入空间划分放宽这个限制（section 5.1）
• 实际操作中，每一次的划分我们都使用一个轴对齐的平面（axis-aligned plane）
  • 对于场景的原体，我们使用一个点来代替
    • 可以是包围盒的中心
  • 这个点只会在选择平面的一侧
• 划分轴
  • 首先我们选择一个轴（xyz）
    • 测试 3 个轴，选出最好的
    • 启发式算法：round-robin，最长的轴
      • rr：根据轴的长度依概率选择划分轴
• 划分平面
  • 选择划分平面的 3 种基本方式
    • 恰好把包围盒空间划分为两半：spatial median split
    • 恰好把原体数目换分为两半：object median split
      • 实用
    • 损失函数：split based on a cost model
      • 试图求得代价函数的局部最优解
      • 因为我们在划分之前无法准确的知道子结点的代价（cost）
      • 我们将子节点都当作叶子节点进行估计

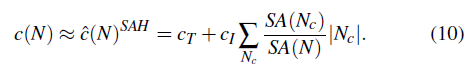
• 推导

\[ \begin{aligned} c(N) &=c(N)^{SAH}\\ &=c_T+\sum_{N_c}\dfrac{SA(N_c)}{SA(N)}c(N_c)\\ &\approx\hat{c}(N)^{SAH}\\ &=c_T+c_I\sum_{N_c}\dfrac{SA(N_c)}{SA(N)}\vert N_c\vert\\ \end{aligned} \]

• 我们也可以把这个当作终止条件的判断标准，如果 \(c_I\vert N\vert\le \hat{c}(N)\) 则停止划分
  • 也就是说，如果把当前节点当作叶子节点的代价比继续划分更小，则停止划分
• 损失函数加上一项，希望子节点的 BVH 重合更少
  • \(V(N)\)：节点 \(N\) 的包围盒的体积
  • \(c_O\)：常数
  • 很直观，就是重合的比例越小越好

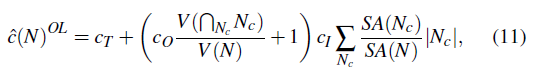
• 这样的损失函数比 EPO 更容易实现，与渲染相关性小，在 BVH 构建的时候便很容易计算
• 以下介绍一些寻找划分平面的算法

sweeping

• 选择划分平面的时候，依次测试所有的可能平面
  • \(N-1\) 个在原体之间的平面
• 计算代价很大，尤其是在算法开始的时候，节点包含的原体数目很多

binning

• 将待划分的轴空间平均的划分为 \(b\) 个区间
• 将所有原体映射到 \(b\) 个区间内部
• 现在我们只需要在这 \(b-1\) 个平面上测试损失函数即可
• 实验表明，一个较小的 \(b(16/32)\) 效果也不错
  • 加速了 bvh 的构建
  • 求交的加速效果和 sweeping 方式差不多
• 随着深度变深，可以使用更少数量的 bin

binning 并行

• 两种并行方式：horizontal parallelization \(\to\) vertical parallelization

• 深度较小：horizontal parallelization（感觉本质上就是并行的桶排序）

  • 少量的内部节点，但是都包含大量的原体

  • 场景的原体被均等分配给不同的线程（\(0\sim T-1\)）

  • 对于每一个线程，将自己的原体映射到 bin 中（\(0\sim B-1\)）

    • 可能存在不同的线程中的原体映射到相同的 bin，因此我们让每个线程新包含一个私有的 bin set，最后做完之后在进行合并
      • 合并过程如下
    • 同时每一个线程 \(t\) 计算 \(N_{L,i,t},N_{R,i,t}\)
      • \(N_{L,i,t}\) 表示对于线程 \(t\) 分到的原体，位于第 \(i\) 个 bin 左边（包含 \(i\) ）的原体数目

  • 做完之后，计算得到 \(t\) 个前缀和 \(N_{L,i}^{t}\)（对所有线程 \(1\sim t\) 求和）

  • 此时每一个线程再扫描一遍它的所有原体，将原体对应的 ID 写到原始的三角形列表中

    • offset 可以从前缀中得到，例如线程 \(t\) 中有 \(a\) 个落在第 \(m\) 个 bin 中，那么这 \(a\) 个原体对应的在三角形列表中的偏移就是如下

    \[ \begin{aligned} &\Big[N_{L,m-1,T-1}+N_{L,m,t-1}, N_{L,m-1,T-1}+N_{L,m,t-1}+a\Big)\\ =&\Big[N_{L,m-1,T-1}+N_{L,m,t-1},N_{L,m-1,T-1}+N_{L,m,t}\Big) \end{aligned} \]

  • 遍历所有的平面，计算最佳划分平面

• 深度较大：vertical parallelization

  • 子树数量和线程数目相当
  • 每一棵子树分配给一个线程

Bonsai 算法

• Bonsai: Rapid Bounding Volume Hierarchy Generation using Mini Trees
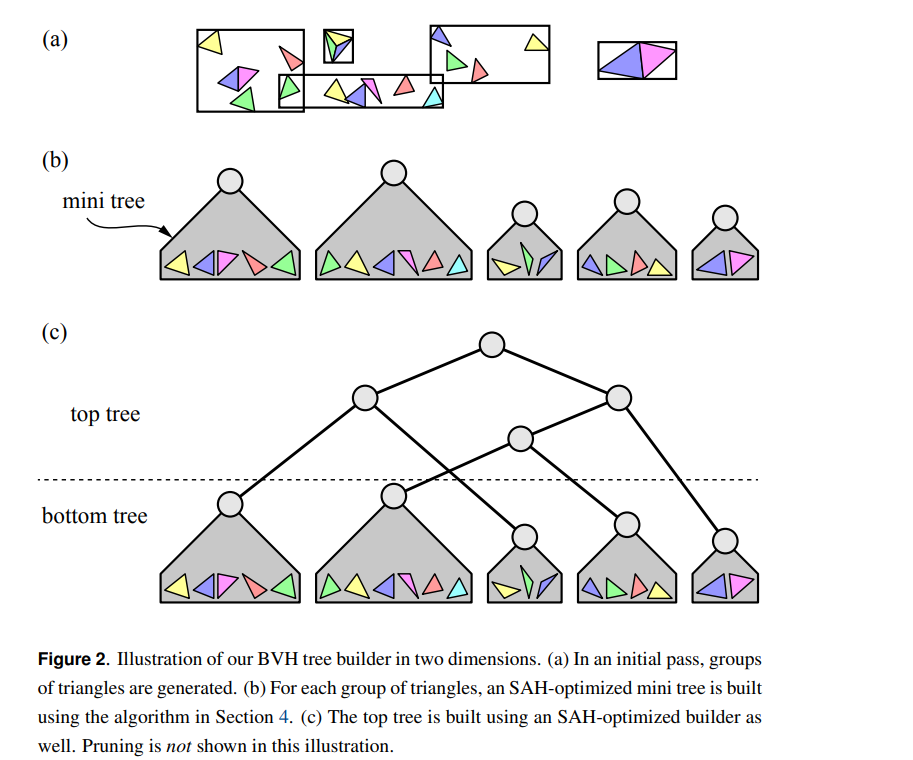
• 算法
  • 首先利用 spatial median split 的方式，将所有的三角形划分为若干个相邻的区域（cluster）
  • 对于每一个区域建立一个 mini-tree，mini-tree 使用 sweeping 的方式建立
  • 之后，将这些区域都看成叶子节点，建立上层的 BVH
    • 论文还提出了剪枝优化

PHR 算法

• progressive hierarchical refinement (PHR)
  • Parallel BVH Construction Using Progressive Hierarchical Refinement

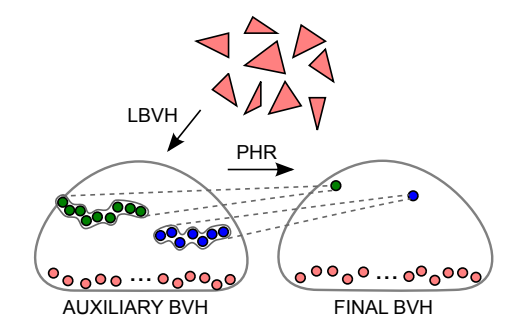
• 算法
  • 首先按照某种方式建立起 BVH（论文是 LBVH）
  • 找到一个 cut（一组节点，这组节点能够将根节点和所有叶子节点分开）
  • 要求这个 cut 满足如下性质
    • 包含的树上的节点数量最少
    • 表面积之和小于一个设定的阈值
  • 对这个 cut，将其划分为两个集合
    • 遍历 3 个轴，使用 sweeping 算法得到最好的划分平面
    • 算的很快，因为节点数目和场景中的原体数目相比很小
  • 此时我们得到两个新的 cut（此时我们建立起了一个两层的 bvh）
  • 对这两个 cut 构建子树（把 cut 内部节点的所有子节点都挂到这个节点上形成一棵树），重复上面的算法（找 cut）
    • 阈值会根据细分的次数进行更新

其他算法

• 更好的近似 EPO 代价函数
• a parallel on-demand construction on the GPU
  • 只构建在遍历过程中可能经过的部分
• 随机采样划分平面
  • Automatic Bounding Volume Hierarchy Generation Using Stochastic Search Methods
• GPU-based
  • binning
  • uniform grids of various resolutions to accelerate binning on GPUs
• 其他的 binning 算法
  • 根据节点的大小进行分类（而不是位置）
• 利用 k-means 的方式构造 BVH，形成 k-分叉的 BVH，然后再聚合

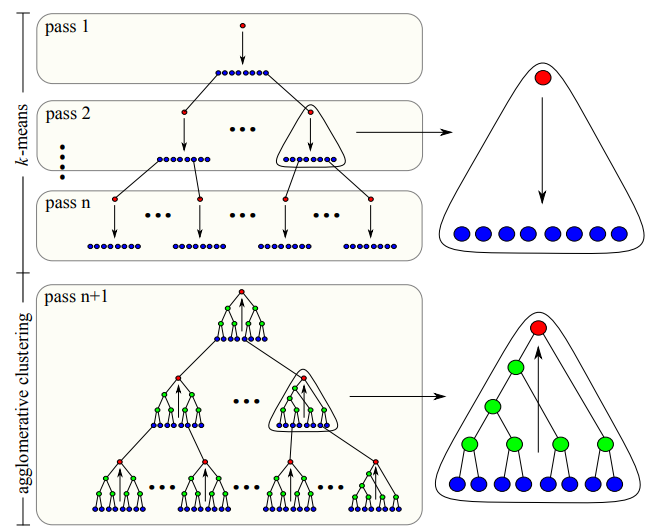
4.2. Bottom-Up Construction

• 聚合算法
  • 最早提出：Fast Agglomerative Clustering for Rendering
• 基本思路
  • 初始的时候，所有的原体都被当做是 clusters
  • 每轮迭代的时候，最近的两个 cluster 会被合并
    • 距离函数：将两个 cluster 都包含的包围盒的表面积
  • 反复迭代，直至只剩下一个 cluster
• 一般而言效果好，但是时间开销极大
• 从算法来看，很容易看出这里的优化主要集中在 bottom 的部分
  • 可能导致 top 部分的优化很差
• 优化的难点：每次迭代都需要对每一个点找最近邻
  • the nearest neighbor search has to be performed for each cluster to determine the closest cluster pair in each iteration

堆与 kd-tree

• 论文：Fast Agglomerative Clustering for Rendering
• 数据结构
  • 堆：以距离为优先级函数保存最近邻
  • 辅助的 kd-tree：加速最近邻的查找
• 伪代码如下

KDTree kd = new KDTree(InputPoints);
MinHeap heap = new MinHeap();
foreach A in InputPoints do {
    Cluster B = kd.findBestMatch(A);
    heap.add(d(A,B), new Pair(A,B));
}

while( kd.size() > 1 ) {
    Pair <A,B> = heap.removeMinPair();
    if (! kd.contains(A) ) {
        // A was already clustered with somebody
    } else if (! kd.contains(B) ) {
        // B is invalid, find new best match for A
        B = kd.findBestMatch(A);
        heap.add(d(A,B), new Pair(A,B));
    } else {
        kd.remove(A);
        kd.remove(B);
        Cluster C = new Cluster(A,B);
        kd.add(C);
        Cluster D = kd.findBestMatch(C);
        heap.add(d(C,D), new Pair(C,D));
    }
}

• 不太容易并行，kd-tree 在合并的过程中会被更新

AAC

• approximate agglomerative clustering (AAC)
  • Efficient BVH Construction via Approximate Agglomerative Clustering
• idea：利用 Morton curve 来限制最近邻搜索的区域
  • Morton curve，section 4.4
• 首先，场景中的原体按照 spatial median splits based on Morton codes 的分割方式进行分割，直到每一棵子树包含的 cluster 数目都小于预先设定的一个值
• 在每一棵子树中对 cluster 进行合并
  • 利用聚合算法进行合并，直到数量比较小（可以不是 1）
• 此时对还没有合并的 cluster 进行合并
  • 不是所有的 cluster 都放到一起合并，cluster 数目都小于预先设定的一个值，会先分成多个
• 反复合并，直到树构建完成

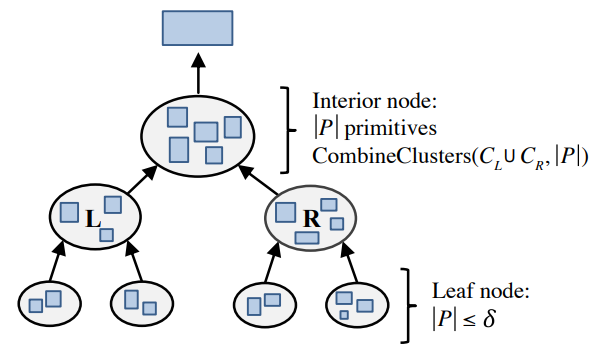
• 每一次合并，为了加速最近邻的查找，使用一个距离矩阵（\(n^2\)）进行 cache
  • 因为每次合并只有少量的距离会被影响

PLOC

• AAC 一开始划分的时候，栈深度较大（导致距离矩阵大）， GPU 不友好
• parallel locally-ordered clustering(PLOC)
  • GPU-based
• idea：距离函数是非减的
  • 如果两个 cluster 的最近邻是相互对应的，那么就可以马上合并
  • 这带来了并行的可能，一次合并所有互相对应的 cluster pair
• cluster 保持在 Morton curve 上的有序性，每次查找最近邻，只查找旁边指定数量的邻居（不需要其他的数据结构，例如距离矩阵）
• 算法
  • 使用 Morton curve 找到每一个 cluster 的最近邻
  • 合并所有的互相是最近邻的节点
    • 移除这些节点，并且将合并后的新节点放到第一个节点原来的位置
  • 使用 parallel prefix scan 的方式移除缺失的部分
• 一般而言，少量几次迭代便能构建出 BVH