(论文)[2021] A Survey on Bounding Volume Hierarchies for Ray Tracing(1)
BVH Survey
banner

1. introduction
- 加速光追方式
- efficient sampling techniques
- denoising methods
- an efficient spatial data structure
- BVH
- Bounding Volume Hierarchy
- 层次包围盒
- 问题:给定一条光线,找到它和场景原体最近的交点
- 光在均匀介质中沿直线传播
2. preliminaries
- 前置知识
- 问题:给定一条光线,找到它和场景原体最近的交点
- 光线:\(\mathbf{o}+t\mathbf{d}\)
- 暴力方法:求出光线和场景中所有原体的交点,取最近的
- 时间复杂度:\(O(n)\)
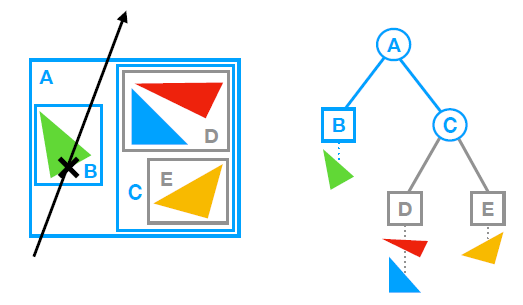
BVH
- k叉有根树
- 叶子节点指向场景中的原体,是包含的原体的包围盒
- 父节点是子结点的包围盒
- 根节点是场景中所有原体的包围盒
- 基于这样一个事实
- 光线和父节点不相交,那么一定和子节点不相交
- 包围盒
- AABB:axis-aligned bounding boxes
- OBB:oriented bounding boxes
- bounding spheres
- 渲染中,场景几何原体一般是 3D 的
BVH 的优点
Predictable memory footprint
- 空间复杂度近似是叶子节点数目的 \(2\) 倍
- 满 \(k\) 叉树总节点 \(N\) 和叶子节点数 \(n\) 有如下关系
\[ N=n+\dfrac{n-1}{k-1}\le 2n-1 \]
Robust and efficient query
- 平均时间复杂度是在 \(\log(N)\) 级别的
- 大多数情况下性能能够和 KD-tree 差不多
- VINKLER M., HAVRAN V., BITTNER J.: Performance Comparison of Bounding Volume Hierarchies and Kd-Trees for GPU Ray Tracing. Computer Graphics Forum (2016)
Scalable construction
- 有很多现成的方法
- 快速建立 \(\longrightarrow\)
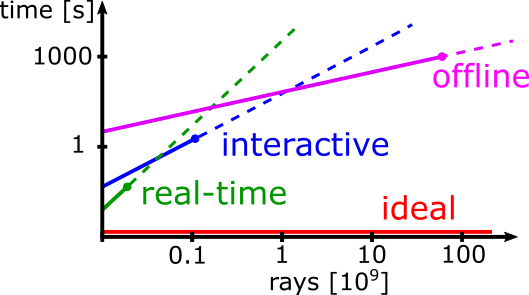
高度优化:trade-off
- construction speed
- BVH quality
- MRays/s
- 实时渲染中,由于时间的限制,只允许投射少量的光线,只能够建立中等质量的 BVH(够了)
- 离线渲染倾向于建立高度优化的 BVH
- 如下图
- 斜率表示质量,截距表示建立的时间开销
Dynamic geometry
- 通过动态调整 BVH 节点实现,传统的 KD-tree 是实现不了的
- 使用 fast BVH construction methods(质量?)
建立 BVH
- 自顶向下建立 BVH 的伪代码如下

求交
- 一般来说有两种需求
- 求出交点:radiance ray
- 判断某一个点是否被遮挡:occlusion ray
- occlusion test
- 使用栈来保存可能有交点的树节点
- 光线和父节点不相交,那么一定和子节点不相交
- 记录当前已经求出来的最近节点位置,用于剪枝
- 记录 \(t\)
- 如果一个包围盒的交点已经比记录的距离远,直接剪枝
- 这个位置必须是和几何原体求交得到的距离(不能是包围盒,可能不和几何原体相交)
- 对于 occlusion test 而言,找到一个交点之后便可以提前停下了(early exit)
- 伪代码如下

- 一次求交的过程
3. cost function
- 对于 BVH 质量的评估,可以使用如下的量表示
- 光线一次求交的平均操作次数
- 根节点的代价函数(递归定义)

- \(\vert N\vert\):当前节点包含的几何原体数目
- \(P(N_c\vert N)\):光线和父节点相交的前提下,子结点 \(N_c\) 和光线相交的概率
- \(c_{T}\):和一个 bvh 节点求交的平均代价
- \(c_I\):和一个几何原体求交的平均代价
- \(c_I,c_T\)
通常是粗略的估计,而不是汇编级的精确值指令数目
- 实际操作很有用
- \(c_T\) 代价很大 \(\Longrightarrow\) 使用更大的 \(k\)(更多分叉,更小深度)
SAH
- Surface Area Heuristic
- 将上面的条件概率转化为几何概率(可计算)
\[ P(N_c\vert N)^{SAH}=\dfrac{SA(N_c)}{SA(N)} \]
- \(SA(\cdot)\) 表示 bvh 节点的表面积

- \(N_i\):以当前节点为根节点的子树的内部节点数目
- \(N_l\):以当前节点为根节点的子树的叶子节点数目
- SAH 的假设(理想的假设,unrealistic)
- 光线的起点在场景包围盒外部均匀分布
- 光线的方向均匀分布
- 光线不会被遮挡
RDH
- ray distribution heuristics
- 对 SAH 不现实的假设的修正,考虑实际光线的分布
\[ P(N_c\vert N)^{RDH}=\dfrac{R(N_c)}{R(N)} \]
- \(R(\cdot)\):击中 bvh 节点的光线数目
- 最早是在 KD-tree 中提出的
OH
- occlusion heuristic
- 在高遮挡条件下,能过够有一个更好的性能
\[ P(N_c\vert N)^{OH}=\dfrac{OC(N_c)}{OC(N)} \]
- \(O(\cdot)\):以当前节点为根节点的子树包含的可见的几何原体的数目
- \(O(N)\) is the number of visible scene primitives in a subtree with root \(N\).
- 这种方法试图将可见的原体和不可见的原体分在不同的 bvh 中
- 如果一个 bvh 中只有(不)可见的原体,则使用 SAH 构建
- 细节见论文
- 单独使用 RDH/OH 可能为导致不稳定
- 由于欠采样、过采样导致的
- 论文中采用和 SAH 进行混合的方法
光源在内部
- 考虑光源在场景包围盒内部
- 例如发反射光的起点便是在内部
- 论文假设:Ray origins are uniformly distributed in space inside S
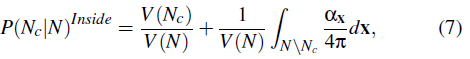
- \(V(\cdot)\):包围盒的体积
- \(\alpha_{\mathrm{x}}\):对于 \(S\backslash N\) 内部的点 \(\mathrm{x}\),bvh 节点 \(N\) 所占的立体角
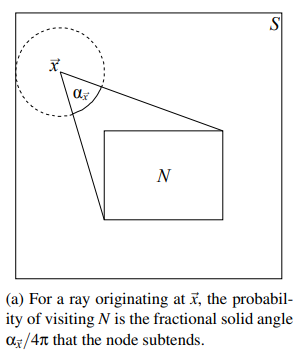
- 公式解释
- 对于光源起点在 \(N\) 内部的光线
- 对于光源起点 \(\mathrm{x}\) 在
\(N\) 外部的光线,可见性的比例就是
\(\alpha_{\mathrm{x}}\)
- 我们假设方向也是均匀分布的
EPO
- end-point overlap heuristic
- 动机:几乎大部分光线都是起源于场景中的某个原体
- 多 bounce 情况下的散射
- 如果光源的起点处在多个分支的包围盒中,那么我们需要全部遍历他们
- If a ray origin (or hit point) is inside multiple branches, we have to visit all of them.
- 惩罚这样的表面,他的位置处于某个 bvh 节点中,但是它本身没有被划分在这个节点中
- 假设三角形可以被拆分(被划分到两个 bvh 中的时候拆分为多个)
- 理想情况下,我们期望没有重叠发生
- 例如一棵所有三角形都被拆分到叶结点的八叉树(octree)
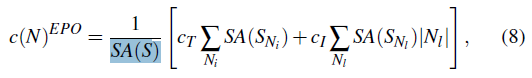
- \(S\):场景中所有几何原体的集合
- \(S_{N}=N\cap S\):在 bvh 节点 N 内部的原体
- 分解惩罚
- \(S^{\ast}_{N}\):位置在当前 bvh 节点内部,而且属于当前节点的原体
- \(S_{N}\backslash S^{\ast}_{N}\):位置在当前 bvh 节点内部,但是不属于当前节点的原体
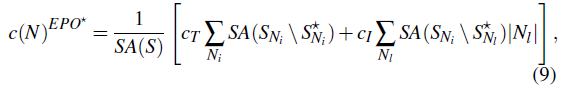
- 实现的时候和 SAH 进行混合
- 如何将其直接用于 bvh 的构建,这个不是很直观