GAMES103.王华民.08.Linear Finite Element Method II(2)

Posted on Edited on In Views:
Hyperelastic Models、有限元模拟的 Hessian 计算、有限元模拟的隐式积分、非线性优化

有限元模拟

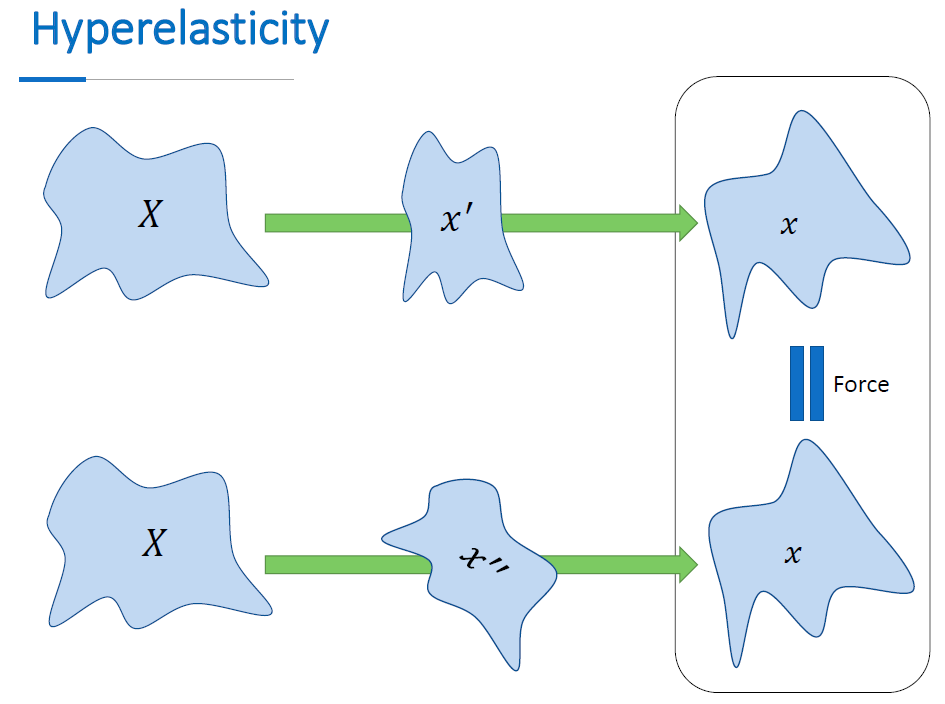
Hyperelastic Models

  • 之前使用的 Stvk 模型存在很多局限性
    • 不能处理反转情况
    • 真实材料力学的工程里面 Stvk 模型使用的很少
    • 图形学中为了简化，使用的比较多
  • 通用模型：Hyperelastic models
    • 通过能量密度推出来的
    • 如何构造一个从 G 到 S（stress）的映射
    • 能量/力与变形过程无关，只与当前时刻的形状有关
    • 可以势能描述

各向同性材料

  • isotropic material
  • first piola-kirchhoff stress 是 \(\mathbf{F}\) 的一个函数

\[ \mathbf{P}(\mathbf{F})=\mathbf{P}(\mathbf{UDV^{\text{T}}}) \]

  • 对于各向同性的材质来说，可以把旋转项提出来
    • F：旋转 + 拉伸 + 旋转

  • principal stretches：主拉伸量
  • 在论文中常常这样描述 \(\mathbf{P}\)

  • 然而这里实际上，由于 \(\text{trace}(\mathbf{AB})=\text{trace}(\mathbf{BA})\)

\[ \begin{aligned} \text{trace}(\mathbf{F}^{\text{T}}\mathbf{F}) &=\text{trace}(\mathbf{UDV^{\text{T}}VDU^{\text{T}}})\\ &=\text{trace}(\mathbf{UD^2U^{\text{T}}})\\ &=\text{trace}(\mathbf{U^{\text{T}}UD^2})\\ &=\text{trace}(\mathbf{D^2})\\ \end{aligned} \]

  • 类似的还有

\[ \begin{aligned} \text{trace}(\mathbf{C}^2) &=\text{trace}(\mathbf{UD^2U^{\text{T}}UD^2U^{\text{T}}})\\ &=\text{trace}(\mathbf{UD^4U^{\text{T}}})\\ &=\text{trace}(\mathbf{U^{\text{T}}UD^4})\\ &=\text{trace}(\mathbf{D^4})\\ \end{aligned} \]

  • 于是不同模型的描述如下

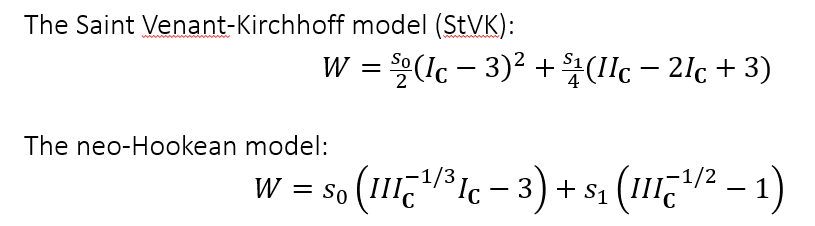
  • 注意这里的 stvk 模型
    • 之前提到的模型长这样

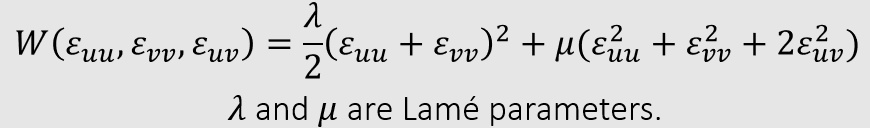
  • 我们可以将其展开，发现 \(\lambda,\mu\) 和 \(s_0,s_1\) 的关系如下（做 lab 3 的时候要注意）
    • 证明方式就是把 \(\epsilon_{uu}\) 等直接展开

\[ s_0={\color{red}\dfrac{1}{4}}\lambda,\;s_1=\mu \]

  • neo-Hookean 模型在真实的材料力学中使用的更多
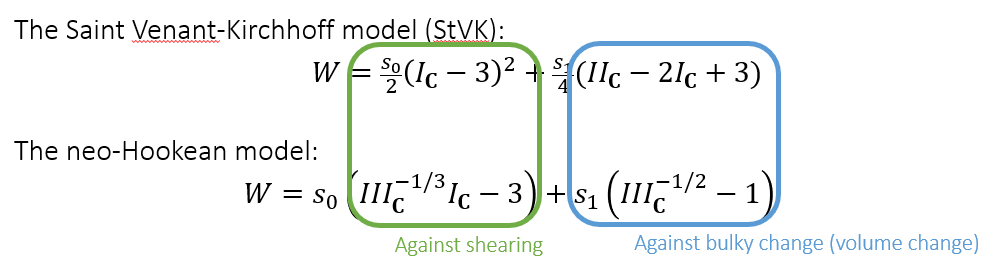
  • 这些模型都有两项
    • 第一项：抵抗拉伸
    • 第二项：阻止体积/面积的改变

  • 其他模型
    • the Mooney-Rivlin model：neo-Hookean 的增强版、模拟橡胶
    • the Fung model：模仿人体组织

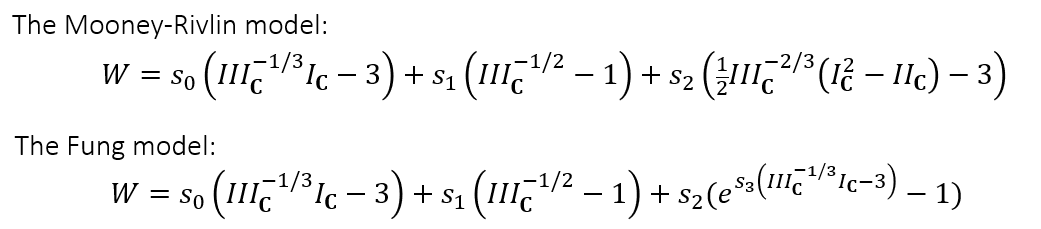
  • 计算 stress

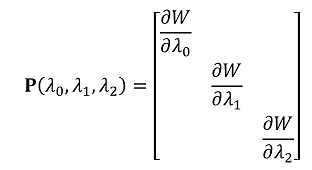
  • 于是对于各向同性的模型，我们可以如下计算

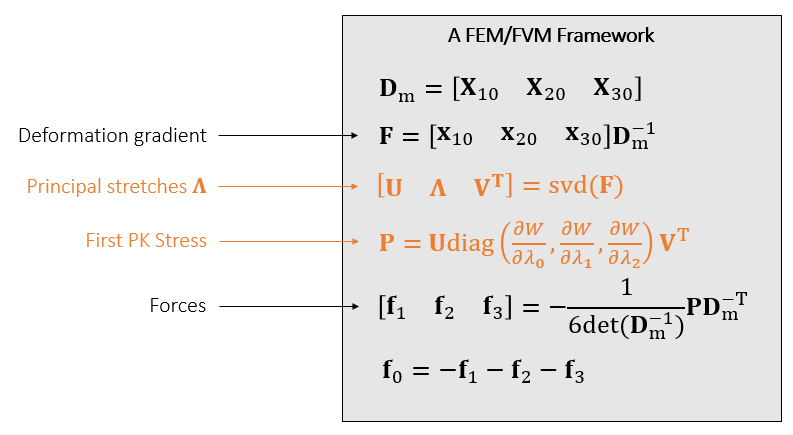
  • 对于同样的模型，这种方法和之前的方法计算结果应该是一样的
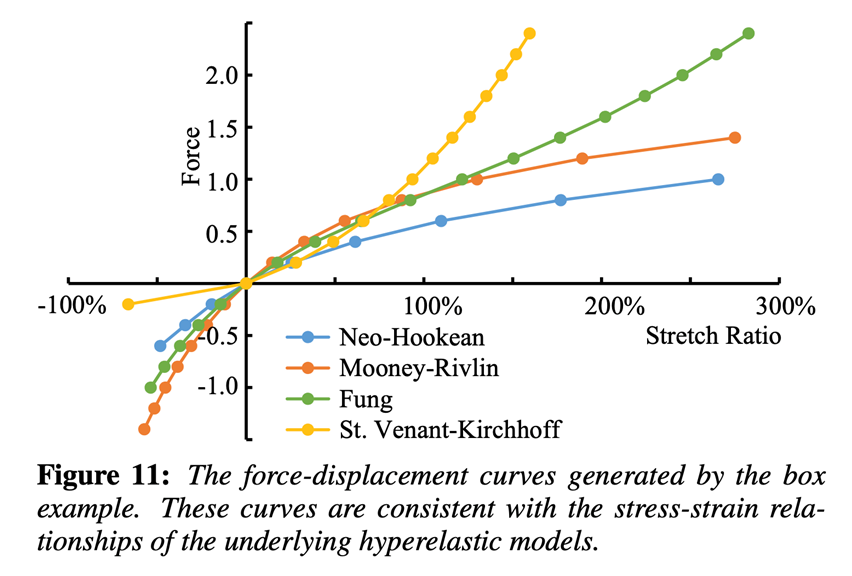
  • Stvk 模型的问题可视化
    • 压缩的时候，压缩到一定程度之后，抵抗力反而变小了
    • 反转之后，不会回到原来的状态，而是反转后的一个平衡状态
      • 反转：四面体的一个顶点跑到它所对的面的另一面去
    • Irving et al. 2004. Invertible Finite Elements For Robust Simulation of Large Deformation. SCA

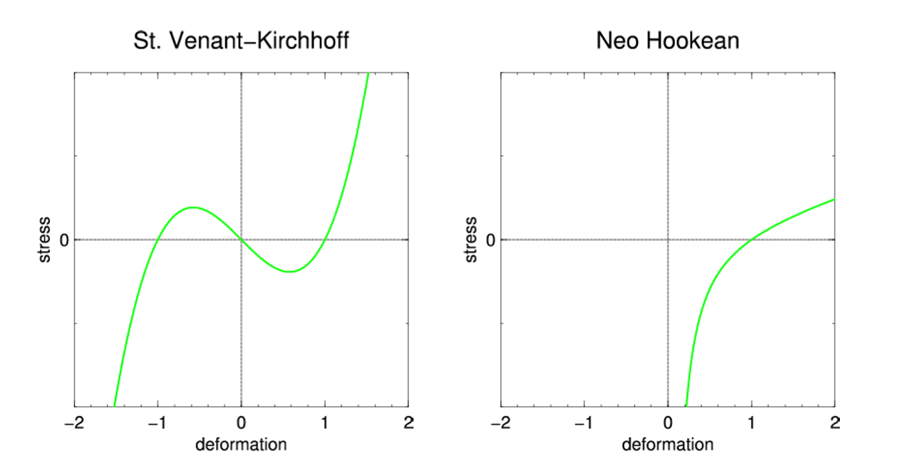
  • 不同模型的模拟
    • Descent Methods for Elastic Body Simulation on the GPU (SIGGRAPH Asia 2016)

  • Poisson Effect：物体被拉伸的时候中间会凹进去
    • 抵抗体积的改变

Hessian(skip)

  • Xu et al. 2015. Nonlinear Material Design Using Principal Stretches. TOG (SIGGRAPH).

  • 计算 Hessian（二阶导）
  • 使用 \(\mathbf{d}_i\) 简化表示，\(V\) 表示体积（前面的那个常数）

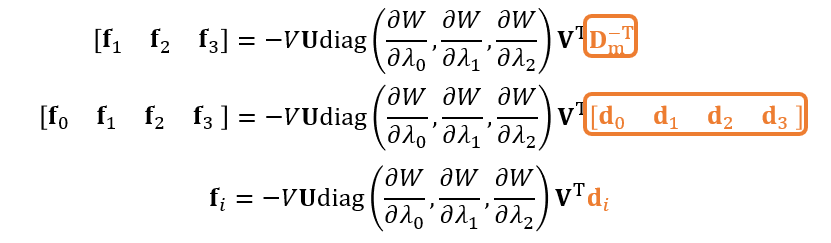
计算过程

  • 绿色部分为常数，可以预计算

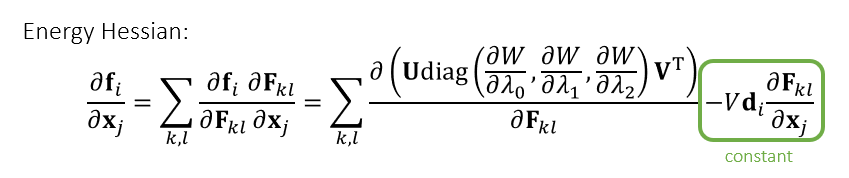
拆解

  • 链式法则计算剩余部分

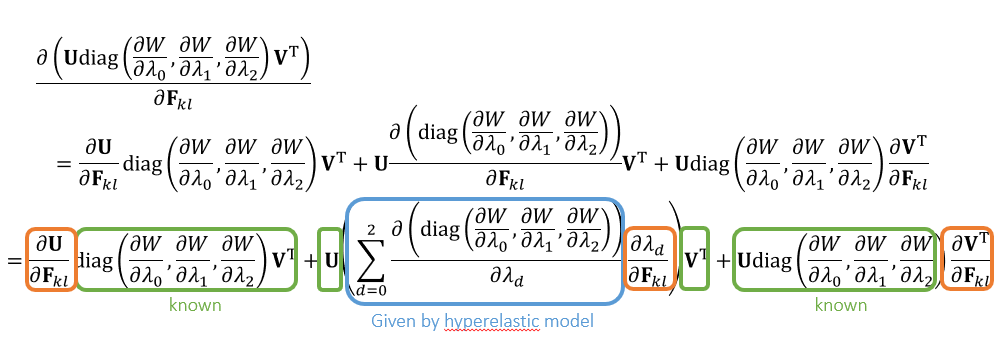
  • 此时只有橙色部分需要计算，其他部分现在都能计算
  • 利用 SVD 分解定义：\(\mathbf{U},\mathbf{V}\) 为正交矩阵，\(\Lambda\) 为对角矩阵
    • \(\mathbf{U}^{\text{T}}\mathbf{U}=\mathbf{I},\mathbf{V}^{\text{T}}\mathbf{V}=\mathbf{I}\)

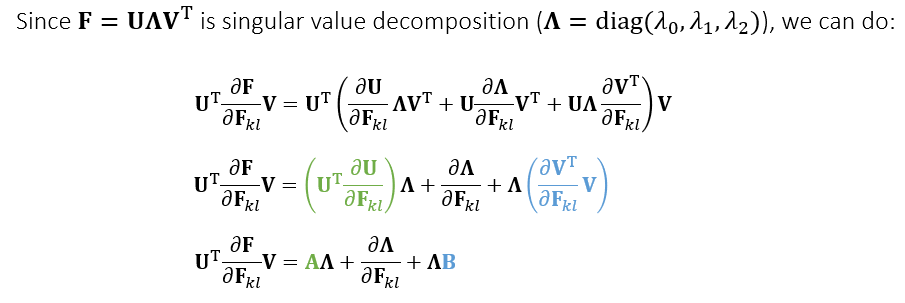
反对称矩阵

  • 如下证明 \(\mathbf{A},\mathbf{B}\) 都是反对称矩阵
    • 反对称矩阵定义如下：\(\mathbf{M}=-\mathbf{M}^{\text{T}}\)

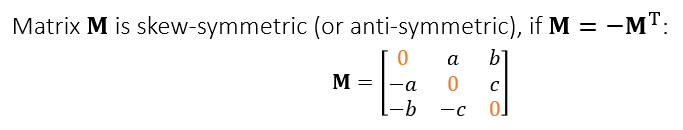
  • 可以由正交性证明

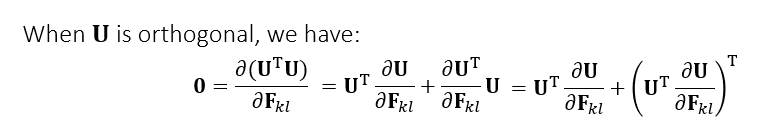
  • \(\mathbf{B}\) 同理

反对称矩阵好处

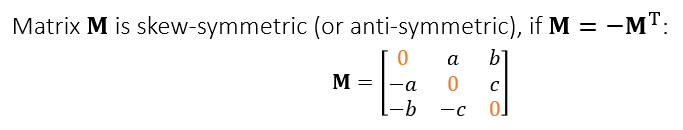
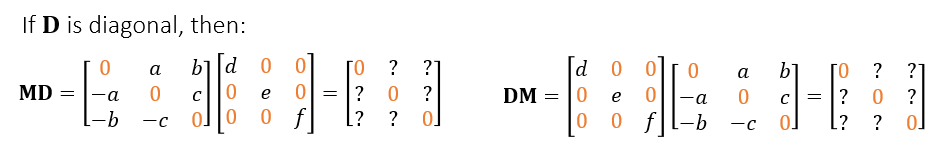
  • 反对称矩阵和对角矩阵的乘积矩阵，对角元都为 0

展开求 A 和 B

  • 回到上面的式子

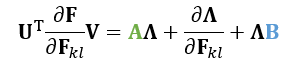
  • 根据反对称矩阵展开

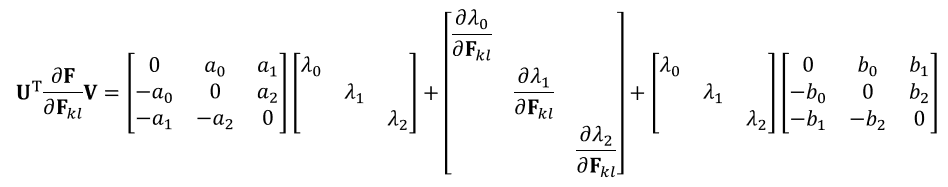
  • 进一步将其计算出来
    • 左边是可以计算的
    • 对应项相等，计算得到 \(\mathbf{A},\mathbf{B}\)（6个变量，6个等式）
    • 同时计算得到了 \(\dfrac{\partial\lambda_d}{\partial\mathbf{F}_{kl}}\)

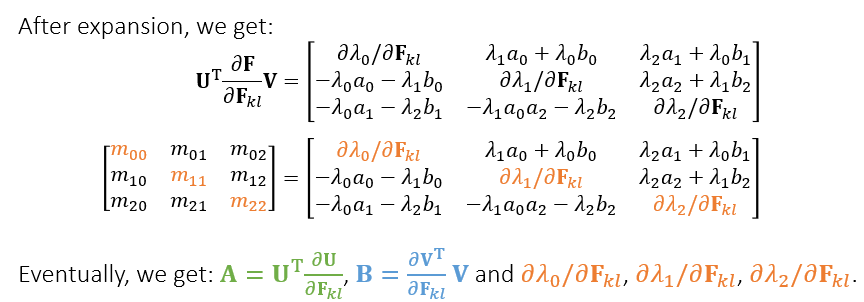
  • 此时返回去，可以把需要求的项都计算出来了，于是我们得到了 Hessian

思路

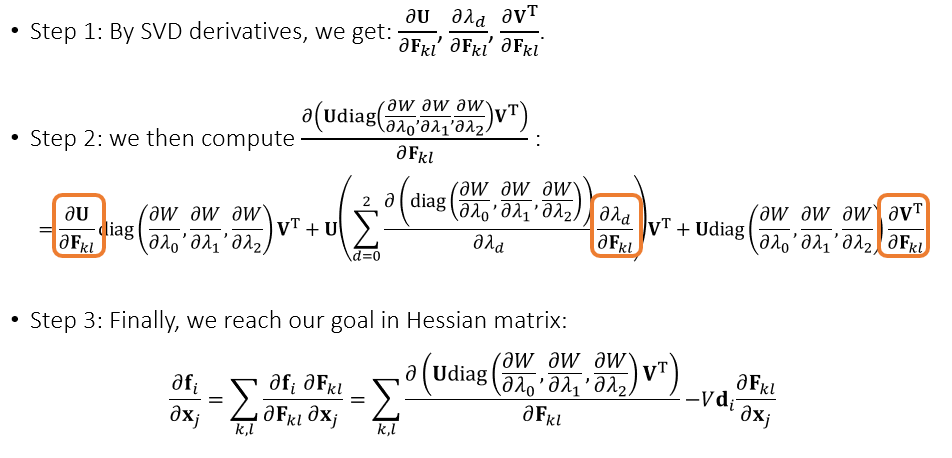
隐式积分(skip)

  • 计算出来 Hessian 之后，思路和之前完全一样

  • 隐式积分

    • 最上面的式子，单独算则是显式积分（不准确），同时求解 \(\mathbf{v},\mathbf{x}\) 则是隐式积分
    • 如果 \(\mathbf{f}\) 仅依赖于 \(\mathbf{x}\)，再根据 \(\mathbf{f}(\mathbf{x})=-\nabla E(\mathbf{x})\) ，则转化为下面的式子
    • 变成最值问题

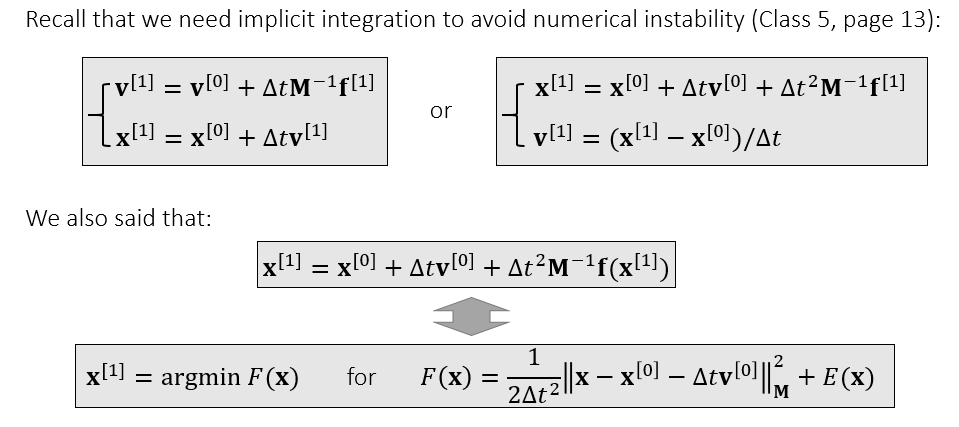
  • 牛顿法求解

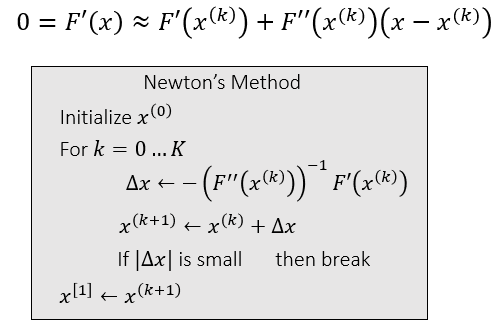
  • 代入 Jacobian 和 Hessian

非线性优化

  • Nonlinear Optimization
  • 现在很多物理模拟都是在做优化，在物理模型上创新不大，基本上都是之前的力学模型
    • GPU、CPU 端的优化
    • 如何让几万个四面体的模型，在 GPU 上能够进行实时模拟

梯度下降方法

  • Gradient Descent

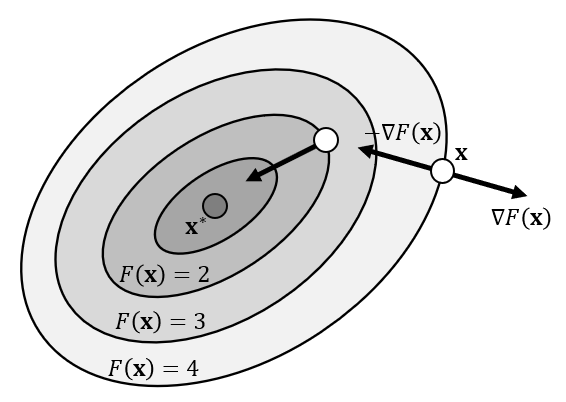
  • 算法流程

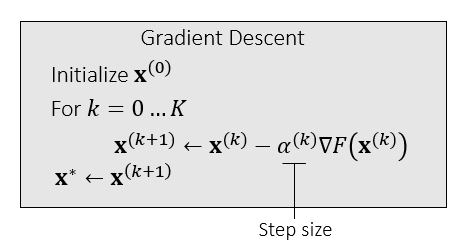
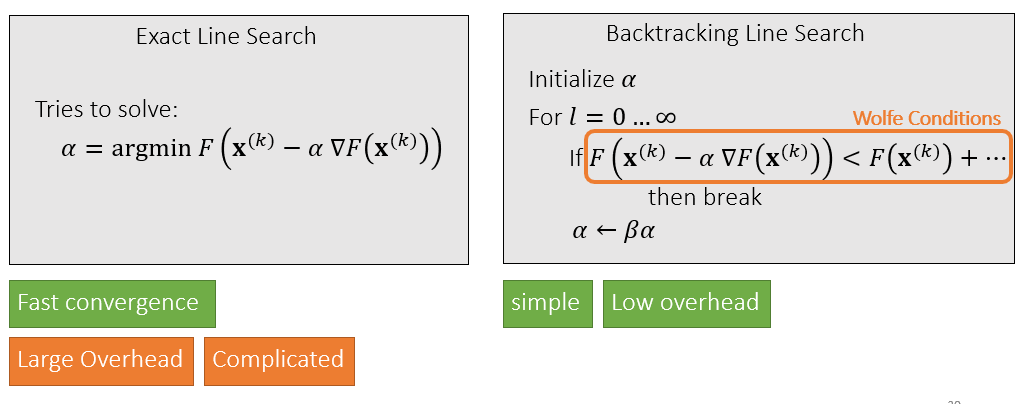
  • 如何找到一个好的步长（step size）是一个困难/重要的问题（critical）
    • 精确解（收敛快、计算代价高）
      • exact line search
    • 近似解（步长尽量大、值要下降）
      • backtracking line search

下降方法

  • Descent Method
  • 负梯度方向不一定是最好的方向

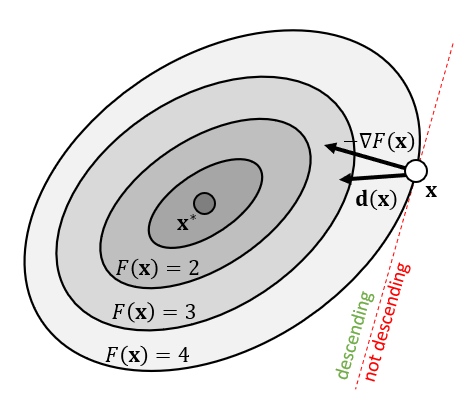
  • 如何找到一个能够下降的方向 \(\mathbf{d}(\mathbf{x})\) ？

\[ F(\mathbf{x})>F(\mathbf{x}+\alpha\mathbf{d}(\mathbf{x})) \]

  • \(\mathbf{d}(\mathbf{x})\) 和负梯度方向在同侧（点积大于 0）

\[ -\nabla F(\mathbf{x})\mathbf{d}(\mathbf{x})>0 \]

  • 目的

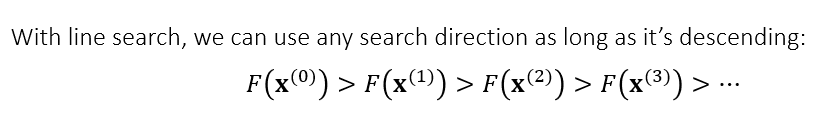
  • 算法流程

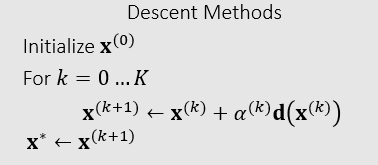
例子

  • 梯度下降法

\[ \mathbf{d}(\mathbf{x})=-\nabla F(\mathbf{x}) \]

  • 牛顿法
    • 要求 Hessian 是正定的
    • 正定矩阵的逆矩阵也是正定矩阵

\[ \mathbf{d}(\mathbf{x})=-\left(\dfrac{\partial^2F(\mathbf{x})}{\partial\mathbf{x}^2}\right)\nabla F(\mathbf{x}) \]

\[ -\nabla F(\mathbf{x})\mathbf{d}(\mathbf{x})=\nabla F(\mathbf{x})\left(\dfrac{\partial^2F(\mathbf{x})}{\partial\mathbf{x}^2}\right)\nabla F(\mathbf{x})>0 \]

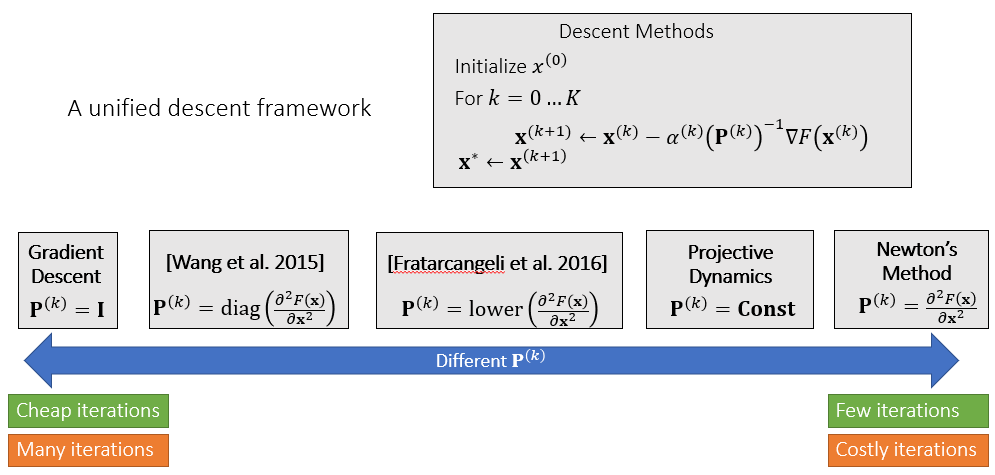
  • 推广，只要 \(\mathbf{P}\) 是一个正定矩阵，如下方法都是一个下降方法
    • 在 lab2 中的衣服模拟，我们使用一个很简单的对角矩阵（正定）也能够使得结果收敛

\[ \mathbf{d}(\mathbf{x})=-\mathbf{P}^{-1}\nabla F(\mathbf{x}) \]

通用框架

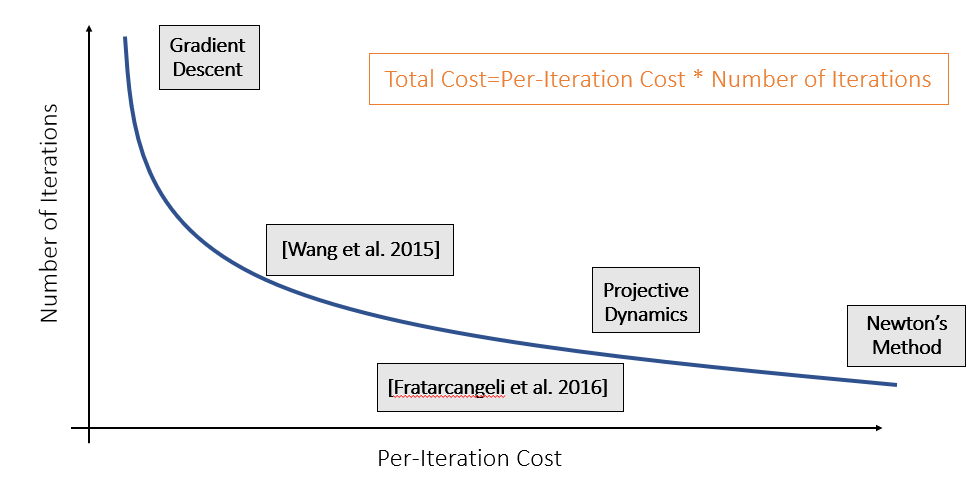
计算代价

  • 总的计算代价 = 每次迭代的代价 \(\times\) 迭代次数

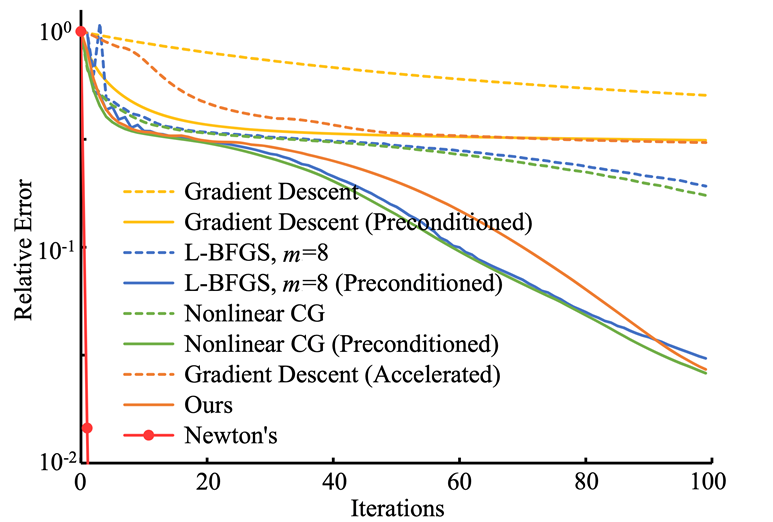
  • 对比
    • Wang. 2016. Descent Methods for Elastic Body Simulation on the GPU. TOG (SIGGRAPH Asia).

其他

  • 真实感的模拟
    • serious 的应用
    • 模拟对真实感的要求很高
    • 例如服装产业，期望和实际成衣在模特上效果一致
    • 设计对比实验
      • 真实的物理实验，参数化特征，量化误差
  • 金属塑性形变一般使用**有限元模拟*