Ray Tracing-The Rest of Your Life(3)

Posted on 2022-03-28 Edited on 2023-09-06 In CG.Kits Views:

直接对光源采样、混合 pdf 采样

Ray Tracing-The Rest of Your Life

Ray Tracing: The Rest of Your Life

8. 直接对光源采样

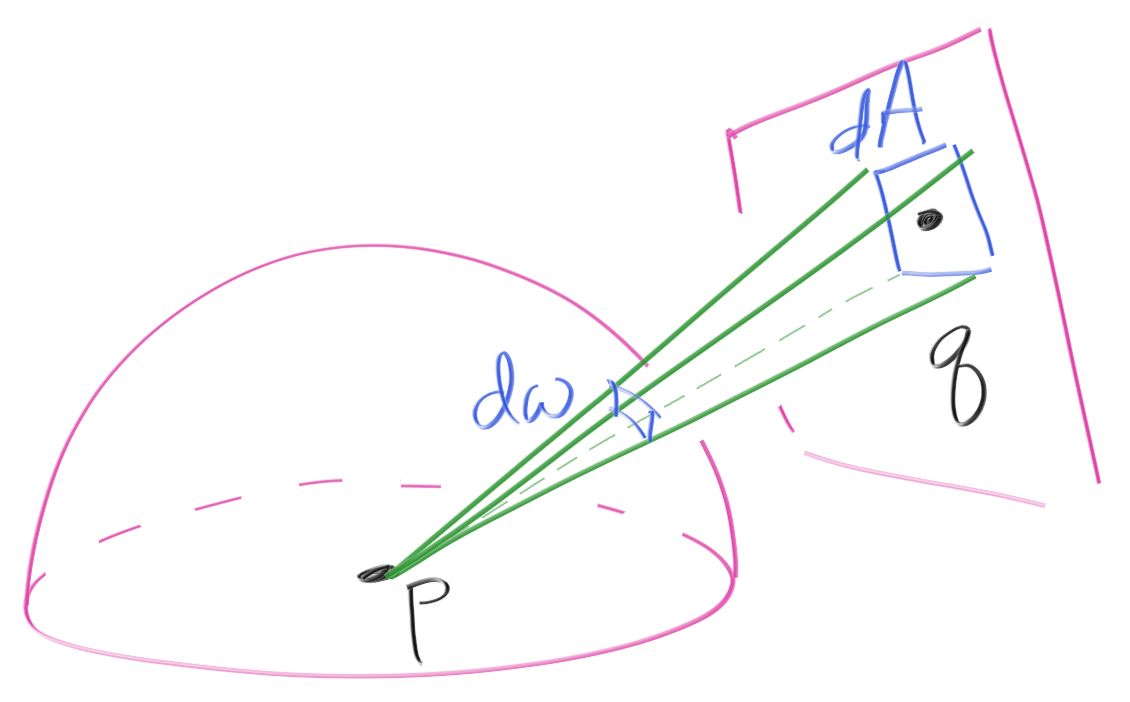
在一块面积为 \(A\) 的区域上均匀采样

\[ p_q(q)\cdot\mathrm{d}A=\dfrac{1}{A}\cdot\mathrm{d}A \]

需要转化到单位球面上

\[ \dfrac{\mathrm{d}\omega}{1^2}=\dfrac{\mathrm{d}A\cdot \cos\alpha}{\text{distance}^2(p,q)} \]

转化为等价在单位球面上均匀采样

\[ p_q(q)\cdot\mathrm{d}A=p(dir)\cdot\mathrm{d}\omega \]

\[ p(dir)\;\mathrm{d}\omega=p(dir)\cdot\dfrac{\cos\alpha}{\text{distance}^2(p,q)}\;\mathrm{d}A=\dfrac{1}{A}\cdot\mathrm{d}A \]

\[ p(dir)=\dfrac{\text{distance}^2(p,q)}{A\cdot\cos\alpha} \]

对比图

常规采样：10spp，2s

直接对光源采样：10spp，1s
- 问题：只有直接光照（1-bounce）

光源边上的亮斑
- 代码中的光源是两面的（two-sided）
- 光源位于屋顶下面一点点（不是完全重合）
如果使用定向光，则不会出现这种情况
- 效果如下

默认的 rect_xz 法向向上，加入 flip_face 包装类，需要修改法向方向

跑一个 1000 spp 看看
- 54s

那确实就变成了实时渲染中的直接光照了（其实也不是，这里的软阴影还是有的hh）
准确的来说，这种方法是有偏的，因为 pdf 的非零值的定义域没有覆盖到整个积分域上
下面这种混合 pdf 则是无偏的，因为其覆盖了整个积分域

9. 混合 pdf

重构 pdf 类

class pdf {
    public:
    pdf() {}
    ~pdf() {}
    // 按照给定的 pdf 返回一个方向
    virtual vec3 generate() const = 0;
    // 返回 pdf(direction)
    virtual double value(const vec3& direction) const = 0;
};

新的 pdf 采样都继承自这个类
例如构造一个朝着某个物体采样的 pdf（hittable_pdf）

混合 pdf

结合对光源直接采样、常规采样
简单使用平均两种 pdf

\[ \text{mixture}_\text{pdf}(dir) = \frac{1}{2} \text{reflection}_\text{pdf}(dir) + \frac{1}{2} \text{light}_\text{pdf}(dir) \]

实现

if (random_double() < 0.5)
    pick direction according to pdf_reflection
else
    pick direction according to pdf_light

vec3 mixture_pdf::generate() const {
    if (random_double() < 0.5) {
        return p[0]->generate();
    } else {
        return p[1]->generate();
    }
}

double mixture_pdf::value(const vec3& direction) const {
    return 0.5 * (p[0]->value(direction) + p[1]->value(direction));
}

效果比较

10 spp

混合 pdf，1s

常规采样：2s

直接对光源采样：1s

1000 spp

直接对光源采样：54s

常规采样：177s

混合采样：117s

10. 架构的建议

上面的混合采样方法，对光源方向给予更大的采样比例，能够让场景收敛的更快
一些问题
- pdf 采样现在是硬编码在 ray_color() 函数里面的，应该是要放到材质里面去
- 镜面材质
- 背景色
- 使用光谱代替 RGB

11. 管理 PDF

放到材质里面去
如何让一种物体有两种材质的效果
- varnished wood：漆木
- 部分 diffuse：木
- 部分 specular：漆
修改不同材质的 scatter() 函数即可
把左边的 box 材质替换为镜面
- 左上角应该是反射（1000 spp）

50000 spp
- 5339s

对球体采样

之前我们只写了对一个长方形采样，现在增加其他的部分
- 修改 object 的 random() 函数
计算 pdf
- 采样一个单位长度的出射方向, 起点在 (0,0,0), 方向和球体有交点
- 在这个立体角内部均匀后采样

求 \(\theta_{\max}\)

\(\theta_{\max}\) 如下图所示

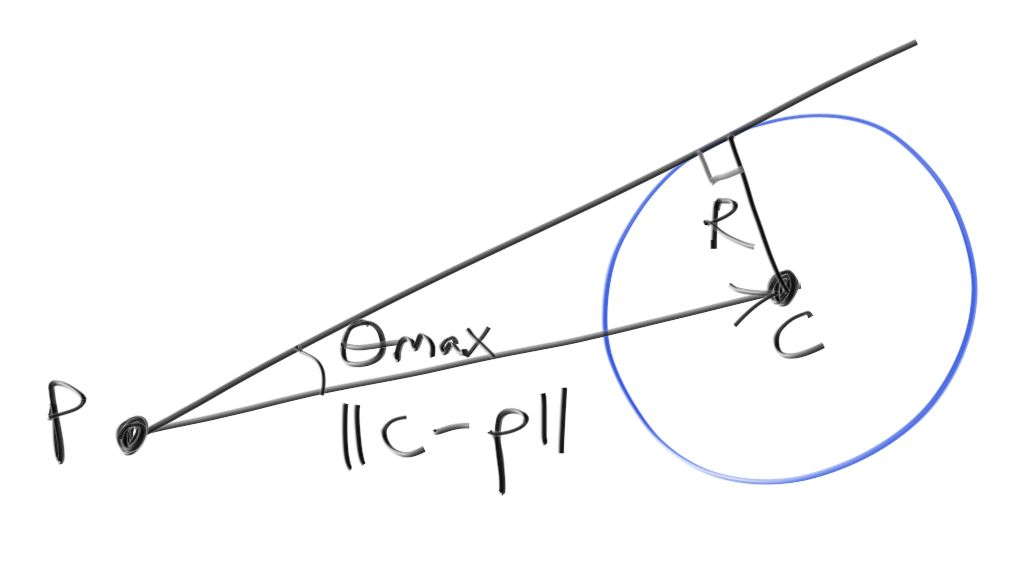\[ \sin(\theta_{\max})=\dfrac{R}{\Vert\mathbf{c}-\mathbf{p}\Vert_2} \]

\[ \cos(\theta_{\max})=\sqrt{1-\dfrac{R^2}{\Vert\mathbf{c}-\mathbf{p}\Vert_2^2}} \]

采样

最大张角为 \(\theta_{\max}\)

\[ f(\theta)=\dfrac{1}{\int_{0}^{2\pi}\int_{0}^{\theta_{\max}}\sin\theta\;\mathrm{d}\theta\mathrm{d}\phi}=\dfrac{1}{2\pi(1-\cos\theta_{\max})} \]

求出对应关系

\[ \phi=2\pi r_1 \]

\[ \begin{aligned} &\Pr(R_2\le r_2)=\Pr(\Theta\le\theta)\\ \Longrightarrow&\;r_2=\int_{0}^{\theta} 2\pi f(t)\sin t\;\mathrm{d}t=\dfrac{1-\cos\theta}{1-\cos\theta_{\max}}\\ \Longrightarrow&\;\cos\theta=1-r_2(1-\cos\theta_{\max})\\ \end{aligned} \]

因此 \(x,y,z\) 表达如下

\[ \begin{array}{c} z = \cos(\theta)=1+r_2(\cos\theta_{\max}-1)\\ x = \cos(2\pi r_1) \cdot \sqrt{1-z^2}\\ y = \sin(2\pi r_1) \cdot \sqrt{1-z^2}\\ \end{array} \]