Stratified Sampling 分层采样
Stratified Sampling
分层采样
- 分层采样就是将采样区域划分为若干个区域,这些区域两两不相交,所有区域的并为原始的积采样区域
- 在不同区域上分配的样本数,和他们区域上的测度成比例
- 此时得到的结果仍然是对原始估计的一个无偏估计,而且方差更小
直观感觉
- 采样的点数没有减少,方差不会变大
- 分组这个操作提供了新的信息
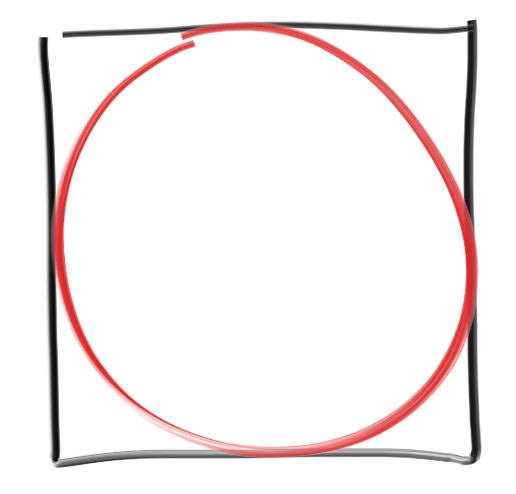
- 想象如下例子,你找的划分恰好把圆划为一部分,剩下的划为一部分,此时 \(I=EI\),方差为 0
例子
蒙特卡洛积分
问题
- 求
pi
- 定义
\[ I=\int_{\Omega}g(X)\rho(X)\;\mathrm{d}X,X=(x,y) \]
- 定义域:\(\Omega\)
\[ \Omega=\{X=(x,y)\vert x^2+y^2\le 1\}\\ \]
- 分布:\(\rho(X)\)
\[ \rho(X)=\left\{\begin{array}{ll} 1,&X\in\Omega\\ 0,&else\\ \end{array}\right. \]
- 函数:\(g(X)\)
\[ g(X)=1 \]
- 一般还有另外一种写法
\[ \rho(X)\;\mathrm{d}X=\mathrm{d}\mu(X) \]
- 实际积分得到:\(I=\pi\)
- 假设 \(p(X)\) 是 \(\Omega\) 上不为 \(0\) 的任意分布,那么对 \(I\) 的蒙特卡洛估计如下
- \(X_i\) 为独立同分布的样本
\[ \hat{I}=\dfrac{1}{N}\sum_{i=1}^{N}\dfrac{g(X_i)\rho(X_i)}{p(X_i)} \]
期望分析
- 这是一个无偏估计
\[ \begin{aligned} E\left[\hat{I}\right] &=E\left[\dfrac{1}{N}\sum_{i=1}^{N}\dfrac{g(X_i)\rho(X_i)}{p(X_i)}\right]\\ &=E\left[\dfrac{g(X_i)\rho(X_i)}{p(X_i)}\right]\\ &=\int_{\Omega}\dfrac{g(X)\rho(X)}{p(X)}p(X)\;\mathrm{d}X\\ &=\int_{\Omega}g(X)\rho(X)\;\mathrm{d}X\\ &=I \end{aligned} \]
方差分析
- 方差如下
\[ \begin{aligned} Var\left[\hat{I}\right] &=\dfrac{1}{N^2}Var\left[\sum_{i=1}^{N}\dfrac{g(X_i)\rho(X_i)}{p(X_i)}\right]\\ &=\dfrac{1}{N}Var\left[\dfrac{g(X)\rho(X)}{p(X)}\right]\\ &=\dfrac{1}{N}\left(E\left[(\dfrac{g(X)\rho(X)}{p(X)})^2\right]-\left(E\left[\dfrac{g(X)\rho(X)}{p(X)}\right]\right)^2\right)\\ &=\dfrac{1}{N}\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{p(X)}\;\mathrm{d}X-\dfrac{I^2}{N}\\ &=\dfrac{1}{N}\left(\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{p(X)}\;\mathrm{d}X-I^2\right)\\ \end{aligned} \]
最小方差分析
- 首先分析:\(g(X)\) 恒非负
- 恒非正同理(\(k\) 取负即可),难的是有正有负
- 首先 \(Var\left[\hat{I}\right]\ge0\),因此如果能够造出一个分布 \(p(X)\) 使得方差为 \(0\),则就是最小值
- 我们如下构造 \(p(X)\)
\[ p(X)=k\cdot g(X)\rho(X) \]
\[ \begin{aligned} &\int_{\Omega}p(X)\;\mathrm{d}X=1\\ \Rightarrow\quad&\int_{\Omega}k\cdot g(X)\rho(X)\;\mathrm{d}X=kI=1\\ \Rightarrow\quad&k=\dfrac{1}{I}\\ \end{aligned} \]
- 此时方差如下
\[ \begin{aligned} Var\left[\hat{I}\right] &=\dfrac{1}{N}\left(\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{p(X)}\;\mathrm{d}X-I^2\right)\\ &=\dfrac{1}{N}\left(\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{k\cdot g(X)\rho(X)}\;\mathrm{d}X-I^2\right)\\ &=\dfrac{1}{N}\left(\dfrac{1}{k}\int_{\Omega}g(X)\rho(X)\;\mathrm{d}X-I^2\right)\\ &=\dfrac{1}{N}\left(\dfrac{I}{k}-I^2\right)\\ &=\dfrac{1}{N}\left(I^2-I^2\right)\\ &=0 \end{aligned} \]
- 因此我们只需要取 \(p(X)\propto
G(X)=g(X)\rho(X)\),就能零方差得到结果
- 这在渲染领域是合理的,渲染的 \(G(X)\) 非负
- 如果有正有负,分析如下
- 有最小值,但不是 \(0\)
- 柯西不等式
\[ \begin{aligned} &\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{p(X)}\;\mathrm{d}X\\ =\quad&\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{p(X)}\;\mathrm{d}X\int_{\Omega}p(X)\;\mathrm{d}X\\ \ge\quad&\left(\int_{\Omega}\sqrt{\dfrac{g^2(X)\rho^2(X)}{p(X)}}\sqrt{p(X)}\;\mathrm{d}X\right)^2\\ =\quad&\left(\int_{\Omega}\vert{g(X)}\vert\rho(X)\;\mathrm{d}X\right)^2\\ \end{aligned} \]
- 取等条件
\[ p(X)\propto \vert{G(X)}\vert=\vert{g(X)}\vert\rho(X) \]
- 方差最小值为
\[ \begin{aligned} Var\left[\hat{I}\right] &=\dfrac{1}{N}\int_{\Omega}\dfrac{g^2(X)\rho^2(X)}{p(X)}\;\mathrm{d}X-\dfrac{I^2}{N}\\ &\ge\dfrac{1}{N}\left(\left(\int_{\Omega}\vert{g(X)}\vert\rho(X)\;\mathrm{d}X\right)^2-I^2\right)\\ \end{aligned} \]
- 使用一个 \(p(X)\) 进行采样,则正比于绝对值已经是最小方差策略
实现
- 如果 \(p(X)\) 为 \(\Omega'\)
上的均匀分布,可以简化如下(代码实现)
- 估计 \(\pi\)
\[ \Omega'=\{-1\le x\le1,-1\le y\le 1\}\\ \]
\[ \hat{I}=\dfrac{1}{N}\sum_{i=1}^{N}\dfrac{g(X_i)\rho(X_i)}{p(X_i)}=\dfrac{4}{N}\sum_{i=1}^{N}g(X_i)\rho(X_i) \]
分层采样
- 简单的来说,对一个区域使用 \(p(X)\)
进行采样的效率,比不上将样本划分给不同区域的采样效率
- \(\pi\) 的例子:整个区域均匀采样 160 个点的效率不如对每个小区域采样 10 个点
- 为了方便描述,利用 \(G(X)\)进行简记, \(G(X)=g(X)\rho(X)\)
- 划分为 \(k\) 个不相交且并集为 \(\Omega\) 的区域:\(\Omega_j\)
- 例如这里划分为
4*4的采样区域
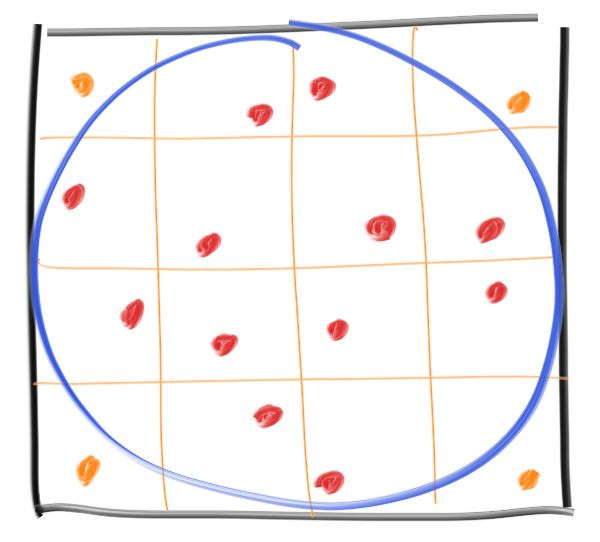
- 采样数:\(n_j\)
- \(N=\sum_{i=1}^{k}{n_j}\)
- \(n_j\) 表示在区域 \(j\) 中采样 \(n_j\) 个样本
- 每个区域的样本数正比于区域内 \(p(X)\) 积分和的大小
\[ n_j\propto \int_{\Omega_j}p(X)\mathrm{d}X \]
- 容易得到
\[ \dfrac{n_j}{N}=\int_{\Omega_j}p(X)\mathrm{d}X \]
- 每个区域内部的采样分布为 \(p_j\),其分布由 \(p\) 决定
- 简单的说就是 \(p\) 在 \(\Omega_j\) 内的分布归一化
- 按比例分配,容易验证 \(p_j\) 积分和为 \(1\),是一个分布
\[ p_j(X)=\left\{\begin{array}{ll} p(X)\cdot\dfrac{N}{n_j},&X\in\Omega_j\\ 0,&else\\ \end{array}\right. \]
- 估计如下
- \(X_{i,j}\) 表示在区域 \(j\) 采样的第 \(i\) 个样本
\[ \begin{aligned} \hat{I}_2&=\sum_{j=1}^{k}\dfrac{1}{n_j}\sum_{i=1}^{n_j}\dfrac{G(X_{i,j})}{p_j(X_{i,j})}\\ \end{aligned} \]
- 这是无偏的,相当于划分定义域,转化为独立的子问题
- 基于黎曼积分的可加性
- \(I_j\) 的定义如倒数第三行
\[ \begin{aligned} E\left[\hat{I}_2\right] &=E\left[\sum_{j=1}^{k}\dfrac{1}{n_j}\sum_{i=1}^{n_j}\dfrac{G(X_{i,j})}{p_j(X_{i,j})}\right]\\ &=\sum_{j=1}^{k}E\left[\dfrac{1}{n_j}\sum_{i=1}^{n_j}\dfrac{G(X_{i,j})}{p_j(X_{i,j})}\right]\\ &=\sum_{j=1}^{k}E\left[\dfrac{G(X_{j})}{p_j(X_{j})}\right]\\ &=\sum_{j=1}^{k}\int_{\Omega_j}\dfrac{G(X)}{p_j(X)}p_j(X)\;\mathrm{d}X\\ &=\sum_{j=1}^{k}\int_{\Omega_j}G(X)\;\mathrm{d}X=\sum_{j=1}^{k}I_j\\ &=\int_{\Omega}G(X)\;\mathrm{d}X\\ &=I \end{aligned} \]
- 方差估计
\[ \begin{aligned} Var\left[\hat{I}_2\right] &=Var\left[\sum_{j=1}^{k}\dfrac{1}{n_j}\sum_{i=1}^{n_j}\dfrac{G(X_{i,j})}{p_j(X_{i,j})}\right]\\ &=\sum_{j=1}^{k}Var\left[\dfrac{1}{n_j}\sum_{i=1}^{n_j}\dfrac{G(X_{i,j})}{p_j(X_{i,j})}\right]\\ &=\sum_{j=1}^{k}\dfrac{n_j}{n^2_j}Var\left[\dfrac{G(X_{j})}{p_j(X_{j})}\right]\\ &=\sum_{j=1}^{k}\dfrac{1}{n_j}Var\left[\dfrac{G(X_{j})}{p_j(X_{j})}\right]\\ &=\sum_{j=1}^{k}\dfrac{1}{n_j}\left(E\left[\left(\dfrac{G(X_{j})}{p_j(X_{j})}\right)^2\right]-\left(E\left[\dfrac{G(X_{j})}{p_j(X_{j})}\right]\right)^2\right)\\ &=\sum_{j=1}^{k}\dfrac{1}{n_j}\left(E\left[\left(\dfrac{G(X_{j})}{p_j(X_{j})}\right)^2\right]-I_j^2\right)\\ &=\sum_{j=1}^{k}\dfrac{1}{n_j}\left(\int_{\Omega_j}\dfrac{G^2(X_{j})}{p_j^2(X_{j})}p_j(X_{j})\mathrm{d}X_j-I_j^2\right)\\ &=\sum_{j=1}^{k}\int_{\Omega_j}\dfrac{G^2(X_{j})}{p_j(X_{j})n_j}\mathrm{d}X_j-\sum_{j=1}^{k}\dfrac{I_j^2}{n_j}\\ &=\sum_{j=1}^{k}\int_{\Omega_j}\dfrac{G^2(X_{j})}{p(X_{j})N}\mathrm{d}X_j-\sum_{j=1}^{k}\dfrac{I^2}{n_j}\\ &=\dfrac{1}{N}\sum_{j=1}^{k}\int_{\Omega_j}\dfrac{G^2(X_{j})}{p(X_{j})}\mathrm{d}X_j-\sum_{j=1}^{k}\dfrac{I_j^2}{n_j}\\ &=Var\left[\hat {I}\right]+\dfrac{I^2}{N}-\sum_{j=1}^{k}\dfrac{I_j^2}{n_j}\\ &=Var\left[\hat {I}\right]+\dfrac{1}{N}\left(I^2-\sum_{j=1}^{k}\dfrac{N}{n_j}I_j^2\right)\\ \end{aligned} \]
- 根据柯西不等式
\[ I^2 =\left(\sum_{i=1}^{k} I_i\right)^2 =\left(\sum_{i=1}^{k} \sqrt{\dfrac{N}{n_j}}I_i\times\sqrt{\dfrac{n_j}{N}}\right)^2 \le\sum_{i=1}^{k}\dfrac{N}{n_j}I_i^2\sum_{i=1}^{k}\dfrac{n_j}{N} =\sum_{i=1}^{k}\dfrac{N}{n_j}I_i^2 \]
- 于是有
\[ Var\left[\hat{I}_2\right]\le Var\left[\hat{I}\right] \]
- 如果 \(p_i\)
是均匀采样,可以简化如下(代码实现)
- 估计 \(\pi\)
\[ \begin{aligned} \hat{I}_2 &=\sum_{j=1}^{k}\dfrac{1}{n_j}\sum_{i=1}^{n_j}\dfrac{G(X_{i,j})}{p_j(X_{i,j})}\\ &=\sum_{j=1}^{k}\dfrac{4}{kn_j}\sum_{i=1}^{n_j}G(X_{i,j})\\ &=\dfrac{4}{N}\sum_{j=1}^{k}\sum_{i=1}^{n_j}G(X_{i,j})\\ \end{aligned} \]
证明
- 上面的期望和方差分析都是一般性的分析
- 书上的证明
- 注意这里的 \(p_i\) 表示的是选到这一个划分区域的概率,而不是上面的 pdf
- 原始蒙特卡洛积分为,积分区域为 \([0,1]^s\)
\[ \int_{\mathcal{L}}\kappa(\mathrm{z})\mathrm{d}F(\mathrm{z}) \]



规范化描述
数值积分
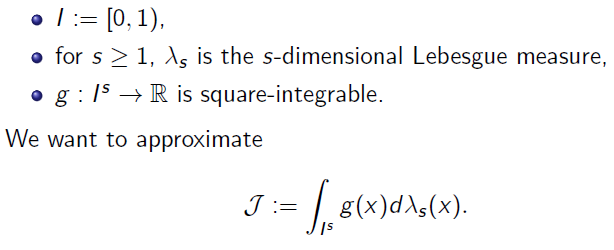
蒙特卡洛积分
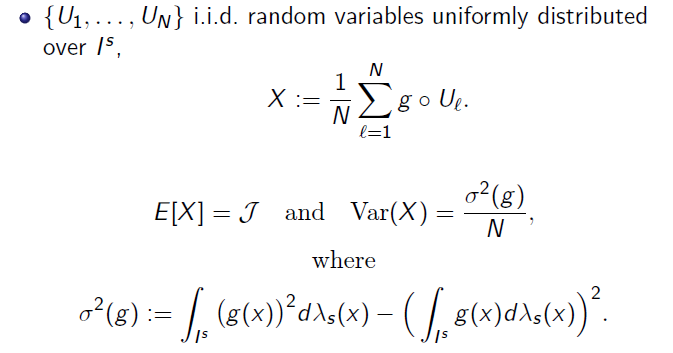
分层积分

参考资料
- 课件
- 书籍:Monte Carlo: concepts, algorithms, and applications
- 4.3 Stratified Sampling
- 图形学|Robust:MC Integration 基础部分+PBRT:MC Sampling 采样算法
- 蒙特卡洛计算中减少方差的技巧