Ray Tracing-The Rest of Your Life

Posted on 2022-03-11 Edited on 2023-06-16 In CG.Kits Views:

蒙特卡洛积分

Ray Tracing: The Rest of Your Life

Ray Tracing-The Rest of Your Life

1. 蒙特卡洛采样

Monte Carlo (MC)

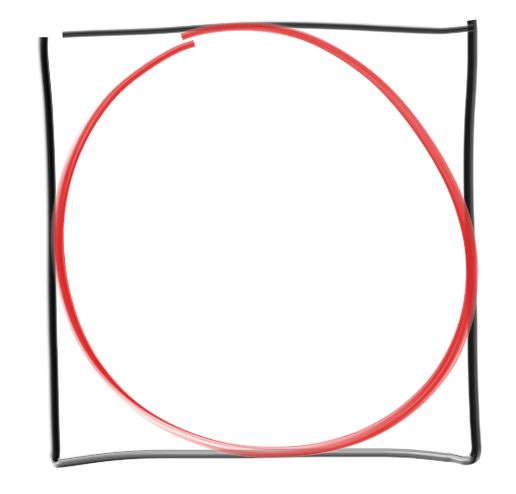\[ \dfrac{\pi r^2}{(2r)^2}=\dfrac{\pi}{4} \]

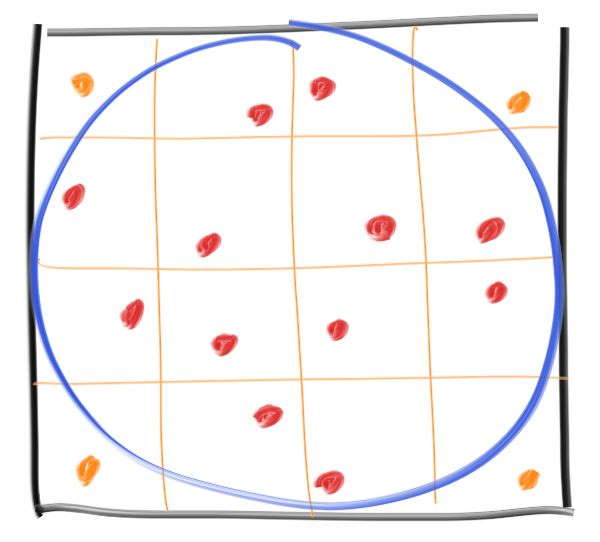
(1) Stratified Samples (Jittering)

我们很快能够得到一个 \(\pi\) 的估计，但是收敛的很慢
- 收益递减定律：law of diminishing return
可以通过分层来降低影响

// 常规的 MC
double x = random_double(-1, 1);
double y = random_double(-1, 1);
if (x * x + y * y < 1) {
    ++circle;
}

// 分层 MC
// 分成了 sqrt_N * sqrt_N 个
x = 2 * ((i + random_double()) / sqrt_N) - 1;
y = 2 * ((j + random_double()) / sqrt_N) - 1;
if (x * x + y * y < 1) {
    ++circle_j;
}

1 2	Regular Estimate of PI: 3.1416273200 Stratified Estimate of PI: 3.1415919200

效果确实好了，估计得更准确，收敛的也更快
- 为什么呢？分层采样的方差更小
- 分层采样的方差分析
这个优势会随着维度的增加而递减，例如把上面的代码应用到 3D 的球和正方体，用体积占比算 PI
- 维度的诅咒： Curse of Dimensionality

2. 一维 MC

例子

\[ I=\int_{0}^{2}x^2\;\mathrm{d}x \]

\([0,2]\) 上均匀采样，\(p(x)=\dfrac{1}{2}\)

\[ \hat{I}=\dfrac{1}{N}\sum_{i=1}^{N}\dfrac{X_i^2}{p(X_i)}=\dfrac{1}{N}\sum_{i=1}^{N}2X_i^2 \]

结果如下：\(\dfrac{8}{3}\)

1
2
3

2.6671368997
2.6669793315
2.6669378018

MC 适用于一些很难显式求出积分的问题，例如

\[ I=\int_{1}^{2}\log(\sin x)\;\mathrm{d}x \]

PDF

pdf：probability density function
- \(p(x)\)

\[ \int_{\infty}^{\infty}p(x)\;\mathrm{d}x=1 \]

cdf：cumulative probability distribution function
- \(F(x)\)

\[ F(x_0)=\int_{-\infty}^{x_0}p(x)\;\mathrm{d}x \]

采样特定分布

如何从一个均匀分布采样得到另外一个分布呢？
目标 cdf 为 \(F(x)\)，目标 pdf 为 \(p(x)\)，\(p(x)\) 在 \([0,1]\) 上非零，\(U\) 表示 \([0,1]\) 上的均匀分布
我们需要找函数 \(f(u(x))\)，使得 pdf 为 \(p(x)\)
设 \(X=f(U)\)

\[ \begin{aligned} F(x)&=\Pr(X\le x)\\ &=\Pr\Big(f(U)\le x\Big)\\ &=\Pr\Big(U\le f^{-1}(x)\Big)\\ &=f^{-1}(x) \end{aligned} \]

于是有

\[ f(x)=F^{-1}(x) \]

于是我们便可以产生指定分布的样本

例子

指定 \(p(x)=\dfrac{x}{2},0\le x\le2\)
\(F(x)=\dfrac{x^2}{4}\)
\(f(x)=\sqrt{4y}\)
样本生成：\(X=2\sqrt{U}\)

void estimate_x_x_pdf() {
    const int N = 100000000;
    double ans = 0.0, ans_pdf = 0.0;
    long long num = 0;
    while (true) {
        ++num;
        double x = random_double(0, 2);
        ans += 2 * x * x;

        x = 2 * sqrt(random_double(0, 1));
        ans_pdf += x * 2;  // x*x/p(x) = x*x*2/x = x*2
        if (num % N == 0) {
            printf(
                "uniform: %.10lf\n"
                "pdf=x/2: %.10lf\n\n",
                ans / num, ans_pdf / num);
        }
    }
}

Importance Sampling

重要性采样
我们期望在积分值比较大的地方采样更多的样本，这样可以得到更小的噪声，而且收敛更快
我们试图将采样引导向分布中比较重要的部分，这也是我们为什么要设计一个非均匀分布采样的原因
- 这被称为重要性采样
例如我们如果令 \(p(x)=\dfrac{f(x)}{\int f(x)}\)，此时 \(E(X)=X,Var[X]=0\)，直接一次采样返回结果

MC 方法流程

一个积分函数

\[ I=\int_{\Omega}G(X)\;\mathrm{d}X=\int_{\Omega}g(X)\rho(X)\;\mathrm{d}X \]

一个在 \(\Omega\) 上不为 0 的分布函数 pdf \(p(X)\)
采样计算结果

\[ \hat{I}=\dfrac{1}{N}\sum_{i=1}^{N}\dfrac{G(X_i)}{p(X_i)} \]

3. 球面 MC

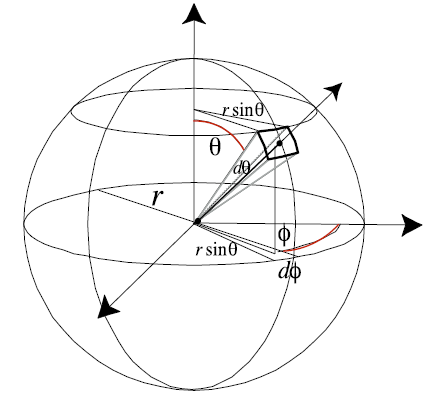
3D 中的方向可以表示为单位球上的一个点

\[ X=(\theta,\phi) \]

考虑球面均匀采样

\[ \int_{\Omega}\;\mathrm{d}S=4\pi \]

\[ \mathrm{d}S=\sin\theta\;\mathrm{d}\theta\;\mathrm{d}\phi \]

例子

\[ I=\int\cos^2\theta\;\mathrm{d}S=\dfrac{4\pi}{3} \]

方法一

均匀采样 \(x,y\)，等价于对 \(\phi,\cos{\theta}\) 均匀采样

vec3 vec3::random_on_unit_sphere_surface() {
    // 如何在一个球面上均匀采样 ? 单位球上的面积(r=1)
    // dA = \sin{\theta}d{\theta}d{\phi} = \cos{\theta}d{\phi}
    // 应该是对 \phi, \cos{\theta} 均匀采样
    double phi = random_double(0, 2 * pi);
    double z = random_double(-1, 1);
    double r = std::sqrt(1 - z * z);
    return vec3(r * std::cos(phi), r * std::sin(phi), z);
}

方法二

\[ I=\int_{0}^{\pi}\left(\int_{0}^{2\pi}\cos^2\theta\sin\theta\;\mathrm{d}\theta\right)\;\mathrm{d}\phi \]

对 \(\phi,\theta\) 均匀采样，此时的估计如下

\[ p(\theta,\phi)=\dfrac{1}{\int_{\Omega}\;\mathrm{d}\theta\;\mathrm{d}\phi}=\dfrac{1}{2\pi^2} \]

代码

// I = \int_{\Omega}\cos^2\theta
void estimate_cos_sphere() {
    const int N = 20000000;
    double ans = 0.0, ans1 = 0.0;
    long long num = 0;
    double const pi4 = pi * 4;
    double const pi22 = 2 * pi * pi;
    double const result = pi4 / 3;
    while (true) {
        ++num;
        // p(x) = 0.5, 0<=x<=2
        vec3 x = vec3::random_on_unit_sphere_surface();
        // p(X) = 1/(4*pi)
        ans += x.z() * x.z() * pi4;

        double theta = random_double(0, pi);
        double phi = random_double(0, pi2);
        double t = cos(theta);
        // p(X) = 1/(2*pi*pi)
        ans1 += t * t * sin(theta) * pi22;
        if (num % N == 0) {
            printf(
                "standard                :   %.10lf\n"
                "dS uniform              :   %.10lf\n"
                "d(theta), d(phi) uniform:   %.10lf\n",
                result, ans / num, ans1 / num);
        }
    }
}

1
2
3

standard                :   4.1887902048
dS uniform              :   4.1888837271
d(theta), d(phi) uniform:   4.1887124194