GAMES103.王华民.07.Other Constrained Methods and Finite Element Method I(2)
有限元方法
- 方法
- The linear finite element method (FEM)
- The finite volume method (FVM)
- Hyperelastic models
- 对于 linear element(三角形、四面体),FEM、FVM 是一样的
FEM
- 这里的例子都是 2D 的
- Linear Finite Element Method
- 线性有限元:对于一个三角形,假定内部的形变是均匀的
- 对于内部形变,可以使用一个统一的公式描述
\[ \mathbf{x}=\mathbf{F}\mathbf{X}+\mathbf{c} \]
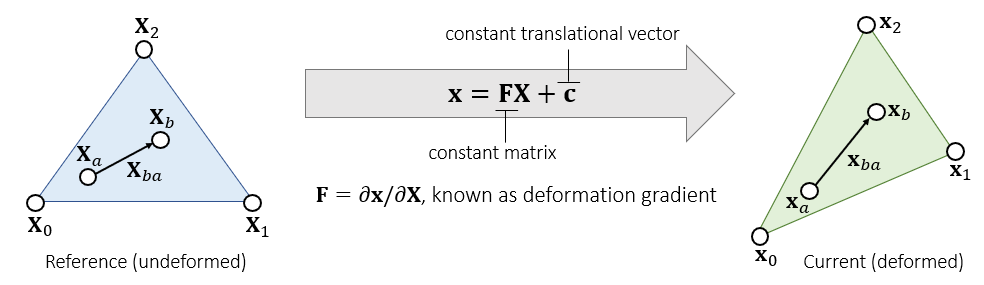
- 对于
- \(\mathbf{F}\):表示形变和旋转
- 形变梯度:\(\mathbf{F}=\partial{\mathbf{x}}/\partial{\mathbf{X}}\)
- \(\mathbf{c}\):表示平移
形变梯度
求解
- 如何求 \(\mathbf{F}\)?
- 对于一条边(两个点),我们有如下结论
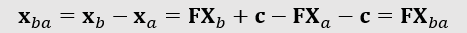
- 通过两条边联立方程组求解

- \(\mathbf{F}\) 中还含有旋转成分,如何去掉旋转成分?
分析
- 形变过程:\(\mathbf{F}=\mathbf{U}\mathbf{D}\mathbf{V}^{\textbf{T}}\)

- 只有 \(\mathbf{D}\mathbf{V}^{\textbf{T}}\)
这两个分量和形变相关
- \(\mathbf{D}\):形变
- \(\mathbf{V}^{\textbf{T}}\):朝着哪个方向形变
- 去掉和形变不相关的成分 \(\mathbf{U}\)?
- SVD 分解之后去除:麻烦、计算量大
- 我们发现
\[ \mathbf{F}^{\textbf{T}}\mathbf{F} =\mathbf{V}\mathbf{D}\mathbf{U}^{\textbf{T}}\mathbf{U}\mathbf{D}\mathbf{V}^{\textbf{T}} =\mathbf{V}\mathbf{D}^2\mathbf{V}^{\textbf{T}} \]
- 定义 Green Strain
Green Strain
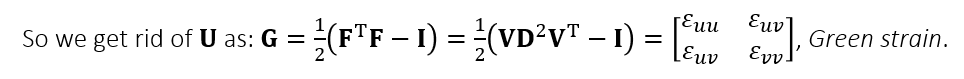
- strain:描述形变的一个量
- 在没有形变的时候为 0
- 大小和形变的大小正相关
- \(\mathbf{G}\)
是旋转无关的
- 加上一个旋转变换 \(\mathbf{RF}\),计算得到的 \(\mathbf{G}\) 还是一样的
- 对称矩阵
能量密度函数
- 利用形变(形变梯度 \(\mathbf{F}\) ),定义能量密度 \(\mathbf{W}(\mathbf{G})\)
- 能量密度:单位面积的能量
- Strain Energy Density Function
- 整个三角形的能量通过积分得到
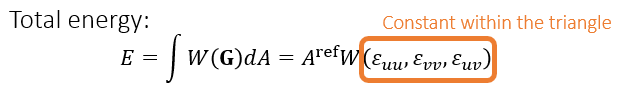
- 三角形内部的 \(\mathbf{F}\) 相同,于是 \(\mathbf{W}(\mathbf{G})\) 也相同
StVK
- Saint Venant-Kirchhoff Model
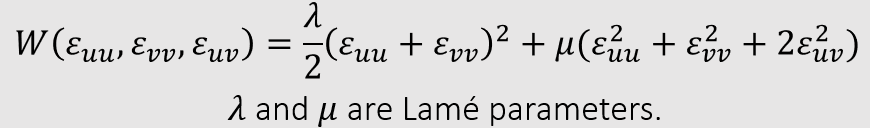
- 物理模拟里面实际上用的并不是很多,图形学中用的多(因为简单)
- 求导
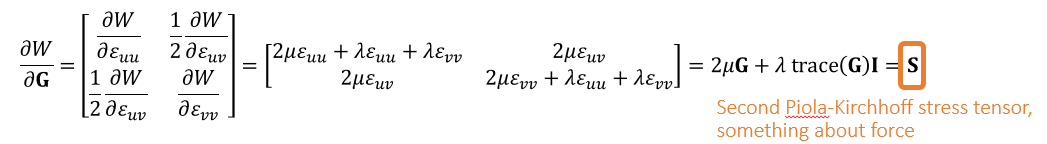
- \(\mathbf{S}\):和力相关
- 问题:如果四面体反转了,没有办法翻回来
求力
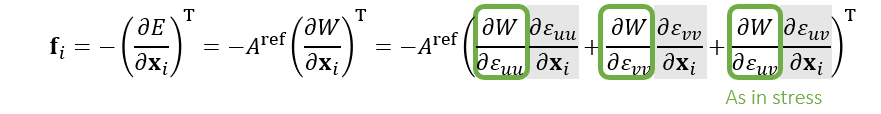
- 绿色部分能够算出来(上面的 \(\mathbf{S}\) )
- 需要求灰色部分
- 从定义出发,推导如下
- a,b,c,d 指代矩阵中的元素

- 上面很复杂!!!
- 但是可以简化成矩阵形式!!!
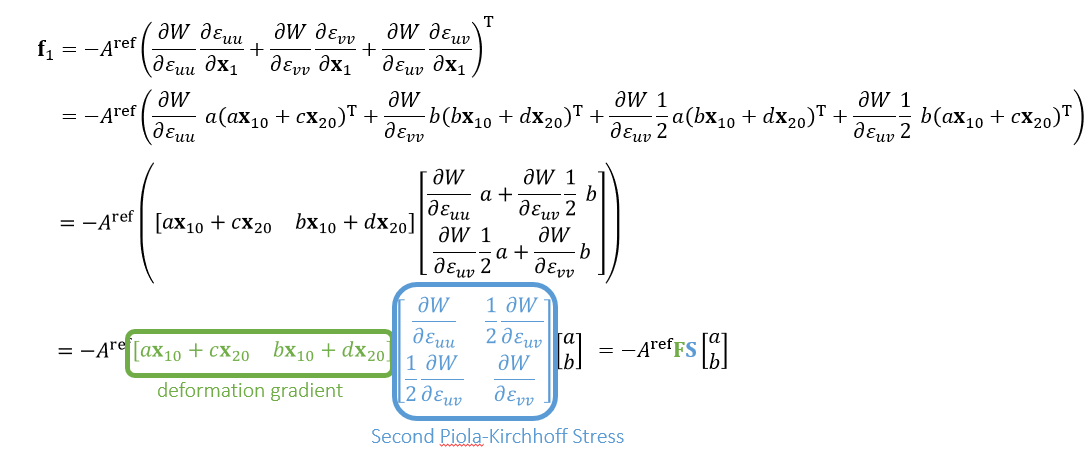
- 另外一个点的力,可以通过合力为 0 求得
\[ \mathbf{f}_0=-\mathbf{f}_1-\mathbf{f}_2 \]
泛化
- 对于 linear element,推导思路都是一样的
实现
- Volino et al. 2009. A simple approach to nonlinear tensile stiffness for accurate cloth simulation. TOG
- 如果对于四面体:所有东西都变为 3 维
其他
- 没有考虑内部的力
- 力是怎么来的?
- 积分得到的,靠近顶点的一块区域里的积分得到,施加在顶点上
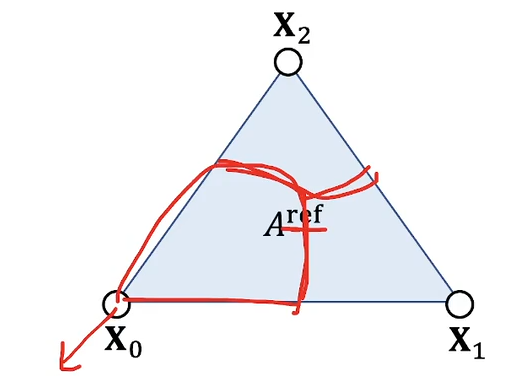
- 衣服的三维模拟,形变梯度是 \(2\times3\) 的矩阵
- 参考状态是二维的,实际状态是三维的
- 目前主流的布料模拟方法
- 弹簧系统 + 隐式积分 + 近似(高分辨率、高质量)
- PBD(低分辨率)