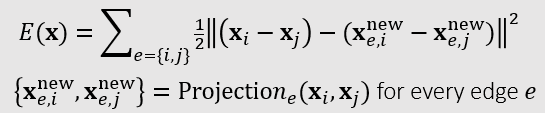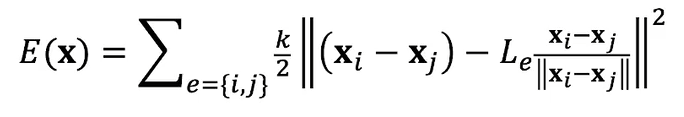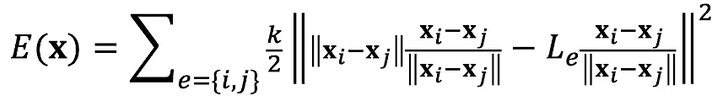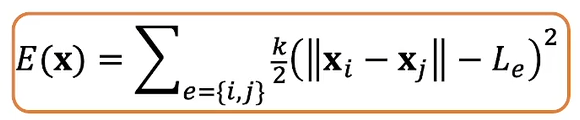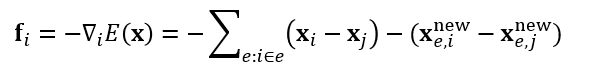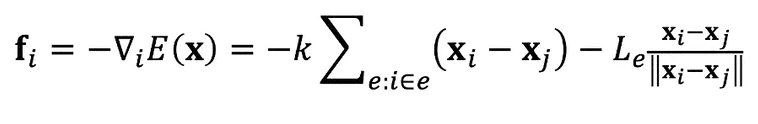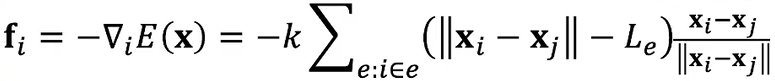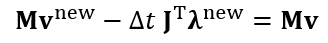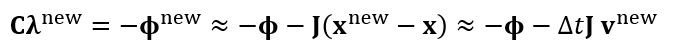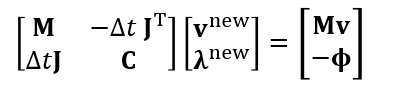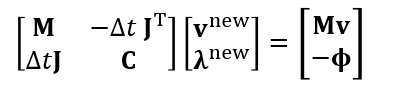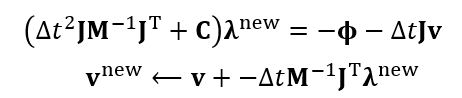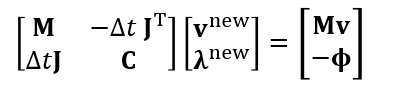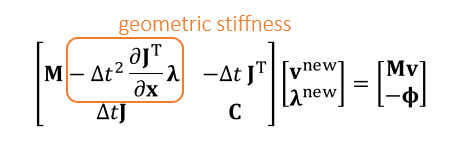GAMES103.王华民.07.Other Constrained Methods and Finite Element Method I

Posted on In Views:
布料模拟、约束方法、Projective Dynamics、Constrained Dynamics、Stable Constrained Dynamics

约束方法

Projective Dynamics

  • PBD 中使用投影函数直接改变顶点位置
  • PD 利用投影函数计算出来的新位置定义一个二次能量函数（而不是直接修改顶点位置），利用构造出来的能量函数进行模拟

三角形

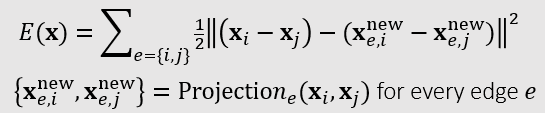
  • 利用 PBD 的投影函数，两个顶点之间的记录计算之后应该就是弹簧原长，进一步变形如下

  • 化简之后发现和弹簧的能量表达形式相同

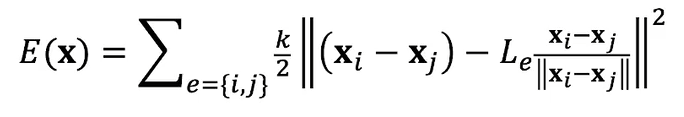
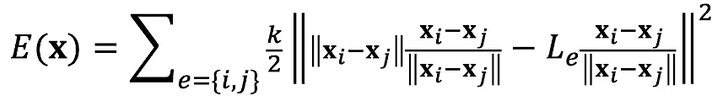
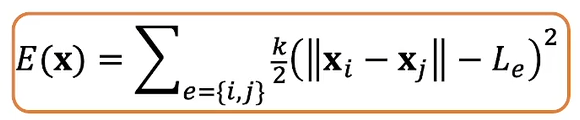
  • 能量对位置求负梯度得到力
    • 假设 \(\mathbf{x}_{e,i}^{\textrm{new}}\) 和 \(\mathbf{x}_{e}\) 无关

  • 根据投影函数

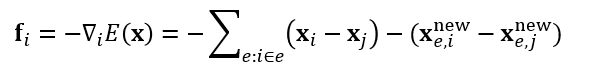
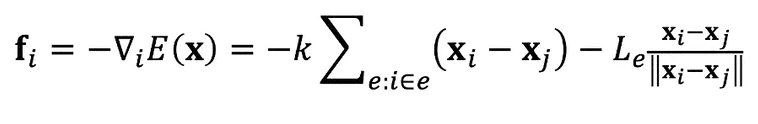
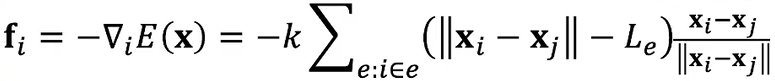
  • 力和弹簧的力也是一样的
  • 因此这个模型和正常弹簧系统的模拟是一样的，只不过引入了两个中间变量 \(\mathbf{x}_{e,i}^{\textrm{new}},\mathbf{x}_{e,j}^{\textrm{new}}\)
  • 为什么使用这个模型而不是原来的弹簧模型？
    • Hessian 不一样

Hessian

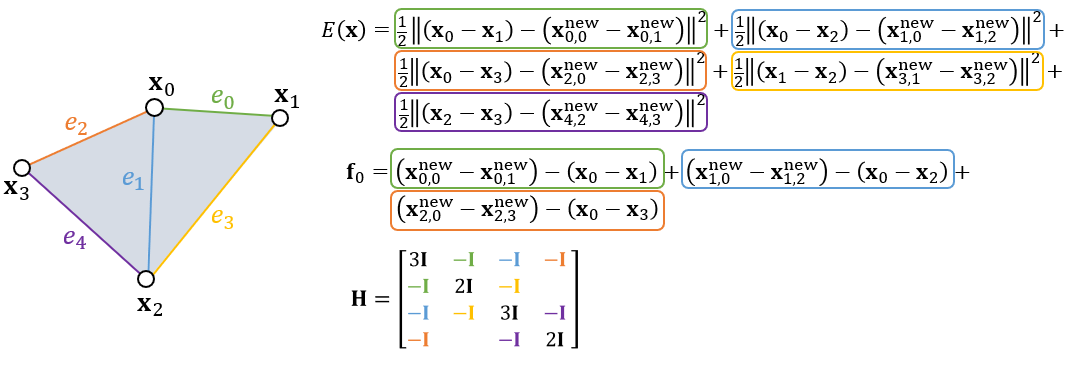
  • Hessian 的可以利用拓扑结构得到（和计算一致）
    • 对角线：从图上看相邻了几条边就是几
    • 非对角线：存的是边，有就是 \(-\mathbf{I}\)，否则为 \(\mathbf{0}\)

PD 的好处

  • 利用上面的假设：假设 \(\mathbf{x}_{e,i}^{\textrm{new}}\) 和 \(\mathbf{x}_{e}\) 无关
  • 能够将 Hessian 简化为一个常数矩阵
    • 常数矩阵能够直接从拓扑结构中得到（和计算一致）
  • Hessian 矩阵是常数之后能够带来大量的计算量上的减少
    • LU 分解求解 \(Ax=b\)
      • 在求解方程组的解的时候，需要进行分解操作（计算量很大）
      • 如果是一个常数的话，对所有方程组求解的只需要分解一次

牛顿法

  • 算法流程和隐式积分差不多，但是在方程组求解的部分简化了计算量
    • 可以理解为就是在隐式积分的过程中，使用了一种方法对 Hessain 矩阵进行了近似
  • PD 利用牛顿法求解如下

  • 对于弹簧系统而言，力的计算和弹簧的力相同，Hessain又是常数，因此投影这一步完全可以省略
    • 有些系统是需要保留投影计算这一步的

Shape Matching

  • 没讲

可行性分析

  • 为什么这样对 Hessian 的计算也可以比较好的模拟？
  • 本质上是对 Hessian 的一个合理近似
  • 效率取决于对 Hessian 近似的好不好

其他

  • 游戏中的布料模拟
    • 例如衣服，更多的是利用人体骨骼驱动，在加上 PBD 的方法
    • 在实际游戏模拟过程中，主要开销是在内存访问上，计算开销并不大
    • PBD 对于内存的访问很少（只需要访问顶点位置），其他方法可能还有一些其他的物理变量需要访问
    • 高性能的优化，内存访问是一个关键

评价

  • 红色：PD

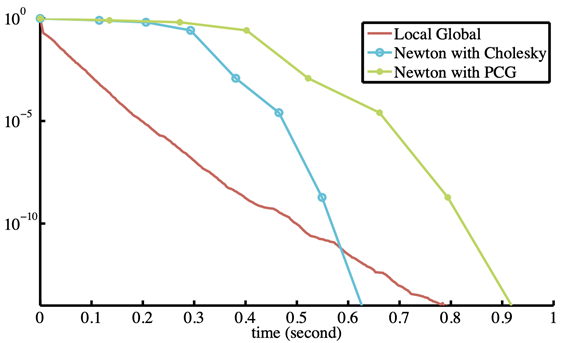
Pros

  • 和 PBD 相比，是有物理含义的
  • 在 CPU 上，作为直接法求解，效率很高（只需要分解一次）
  • 在前几次迭代过程中收敛很快

Cons

  • GPU 上比较慢
    • LU 分解在 GPU 上不太合适
    • 直接法在 GPU 上支持的都不太好
  • 整体而言，收敛的比较慢（假设中没有考虑 projection 导致的 Hessian）
  • 约束改变之后，修改起来比较麻烦（Hessain 矩阵需要修改）
    • 例如破碎 fracture

论文

  • Bouaziz et al. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. TOG (SIGGRAPH).

Constrained Dynamics

  • 为了处理非常 stiff 的约束
    • 更多的用在刚体模拟
    • 例如人体的约束，大臂和小臂连接点的限制（这个约束很强，必须要满足，否则很诡异）
  • 预先引入一个新的变量 \(\mathbf{\lambda}\)，这样能够处理非常 stiff 的情况

转换

  • 约束还是一样

  • 能量写成矩阵形式，力也一样

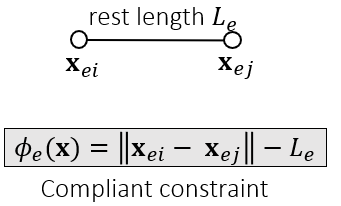
  • 之前做隐式积分只有一个变量，现在有两个（\(\mathbf{x}/\mathbf{v},\mathbf{\lambda}\)）
  • 动量守恒：冲量 = 动量的变化量

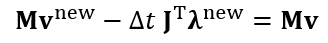
  • 近似
    • 泰勒展开
    • 位置变化量 = 速度 \(\times\) 时间

  • 把上面两个约束放到同一个矩阵中（一起更新）

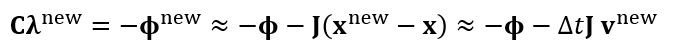
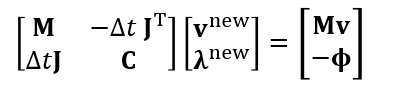
求解

Method 1

  • primal dual method：两个变量一起求解
  • 直接求解矩阵

  • 系数矩阵不一定是正定的

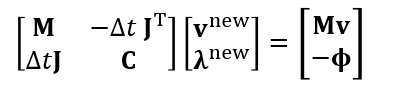
Method 2

  • 消元，先求解 \(\mathbf{\lambda}^{\textrm{new}}\)

  • 消元不一定很简单

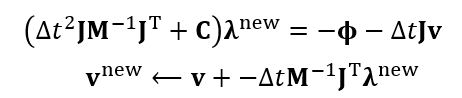
好处

  • stiffness 很大的时候，\(k\to\infty\Longrightarrow\mathbf{C}\to\mathbf{0}\)
  • 原来 \(k\to\infty\) 不好模拟，但是 \(\mathbf{C}\to\mathbf{0}\) 让模拟更简单了

应用

  • Articulated Rigid Bodies (ragdoll animation)
    • 假设人体是有很多刚体构成的，刚体和刚体之间有很多约束

Stable Constrained Dynamics

  • 没讲

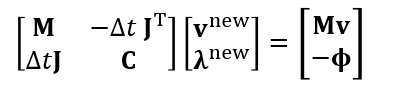
  • 上面矩阵求解如果把 \(mathbf{\lambda}\) 消去之后，则和隐式积分相同，但是 Hessian 有一部分消失了，如果把这部分加上去，模拟会更加稳定

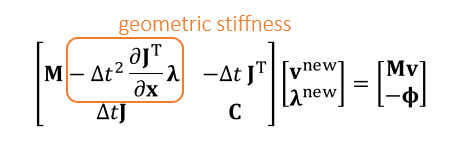
推导

论文

  • Tournier et al. 2015. Stable Constrained Dynamics. TOG (SIGGRAPH).

对比