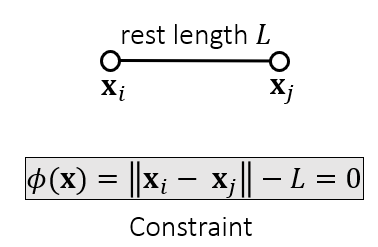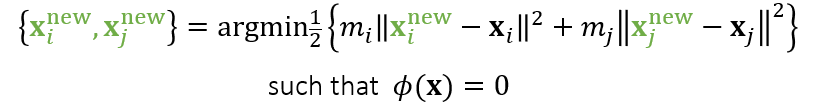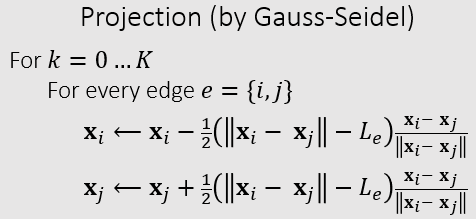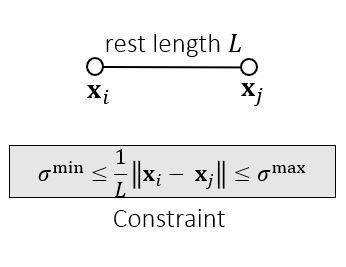0%
约束方法
- 在现实生活中,布料对于拉伸的抵抗比较强,只能有少量拉伸
- 简单的调大弹性系数 \(k\)
会带来如下问题,导致计算量变得很大
- 显示积分不稳定
- 隐式积分中的线性系统会变成病态的(ill-conditioned)
- 约束方法就是为了解决拉伸的问题而被提出的
一根弹簧
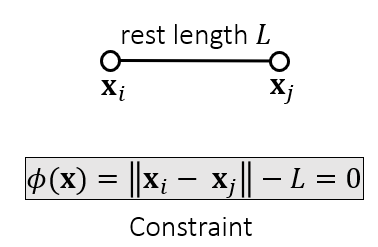
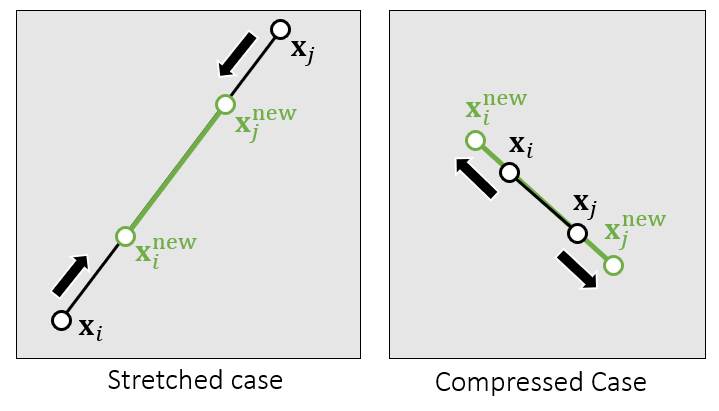
- 投影问题描述如下
- 两个点是 6 维的,看成 6 维空间中的一个点,我们需要将这个点移动到 6
维空间中的可行区域中,而且需要让移动距离尽可能小
- 图示
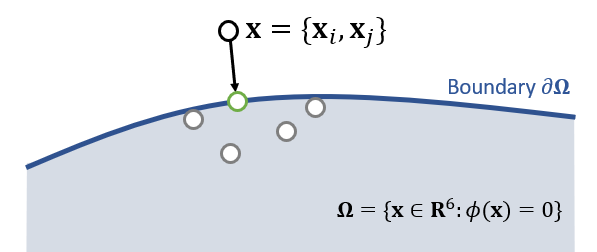
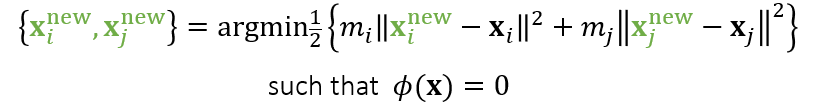
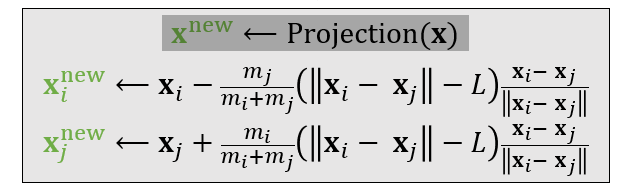
- 代入验证,新位置满足约束条件
- 质量设置
- 为了方便,一般设置为相同
- 固定点,质量设置为无穷大
多根弹簧
Gauss-Seidel Approach
- 高斯塞达尔方法(A Gauss-Seidel Approach)
- 分别处理每根弹簧
- 因为处理完一根弹簧之后,会影响其他弹簧的位置,因此是一个反复迭代更新的过程
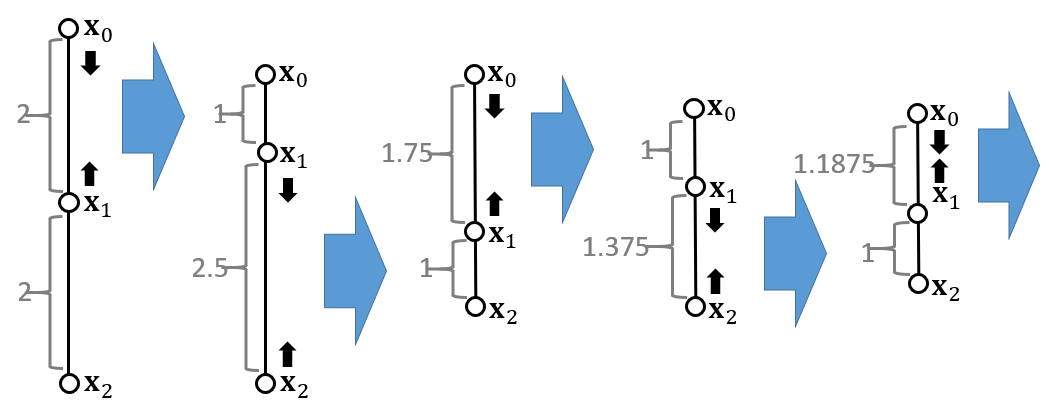
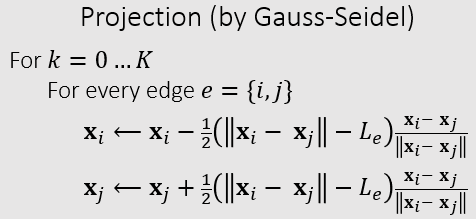
- 无法保证所有边都满足限制,但是迭代次数越多能够尽可能让更多边满足
- 循环的时候,边的顺序会影响计算结果
- 可能会造成偏向性(artifact)
- 可能会影响收敛速度
Jacobi Approach
- 两个目的
- 减少由于边的顺序带来的 artifact
- 尽可能可以并行(更容易并行)
- 思路:每条边计算得到的偏移量不直接更新,而是记录下来,最后计算完了再加权更新
- 算法如下

PBD
- Position Based Dynamics
- 基于上面的投影函数提出的算法

特点
- 没有能量、力的概念
- 弹性系数是由一些非物理因素控制的
- 迭代次数:迭代次数越多,约束满足的越好,显得弹性系数很大(硬)
- 网格分辨率:顶点数量很少,则能够很快收敛,显得弹性系数很大(硬)
- 速度更新很重要
- 这样的方法还可以适用于其他约束
评价
Pros
- 很容易并行,适合于 GPU
- 容易实现
- 低分辨率下运行很快
- 通用性很强
Cons
- 没有什么物理含义,不是物理准确的
- 高分辨率下运行慢
- 层次结构
- Hierarchical approaches (can cause oscillation and other issues…)
- Muller. 2008. Hierarchical Position Based Dynamics.
VRIPHYS.
- 加速方式(Chebyshev)
评价
- 适合游戏开发中低分辨率的网格衣服的模拟
- 低精度实时模拟
Strain Limiting
- 整个思想的提出比 PBD 要早
- 但是这个方法可以认为是 PBD 的改进版
- 和 PBD 类似,但是 Strain Limiting 只是使用 projection function
进行纠正
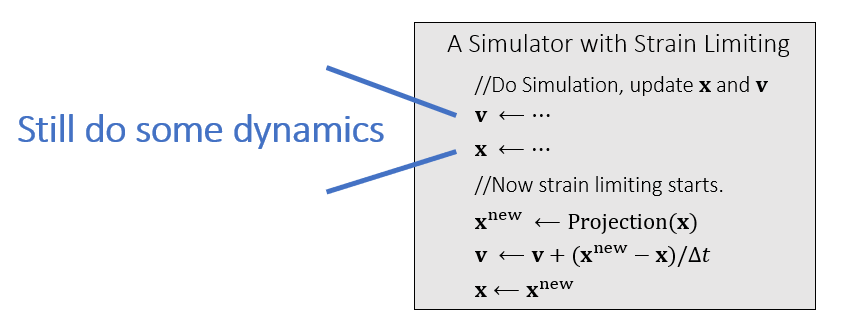
弹簧
- Spring Strain Limit
- strain:描述形变的量 \(\sigma-1\)
- 定义拉伸比例(stretching ratio)
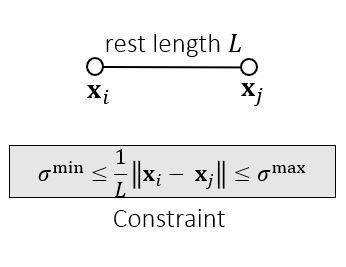

- Why Strain Limiting?
- 模拟很多面料在拉伸到一定程度之后变得很 stiff 的情况
- 让数值模拟的过程更稳定
三角形面积
- Triangle Area Limit
- 思路和上面差不多
- 约束条件
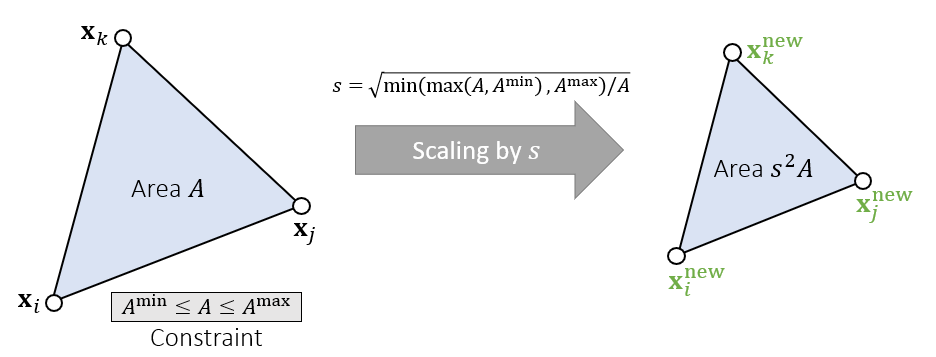

- 质心不变
- 数学上:三个顶点的运动量最小
- 物理上:没有新的动量,不会因为约束而产生奇怪的运动
评价
- 可以保证在模拟的过程中不发生大形变
- 可以模拟布料在形变比较小的时候可以被拉伸,拉伸到一定程度之后变得
stiff 的效果
- 另外一种方式:形变比较小的时候使用上面的模型,比较大的时候使用
strain limiting
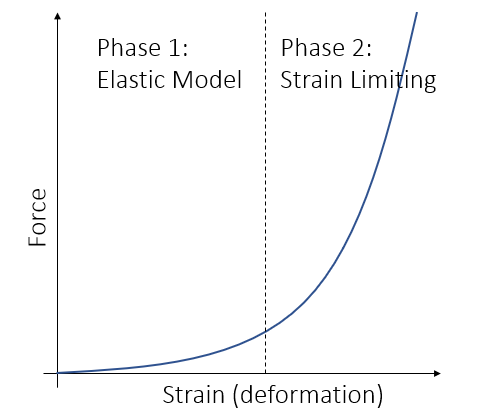
- 能够帮助解决 locking issue
- 第一个阶段使用比较小的弹性系数进行模拟(减轻 locking issue)
论文
- Provot. 1995. Deformation Constraints in a Mass-Spring Model to
Describe Rigid Cloth Behavior. Graphics Interface.(optional)