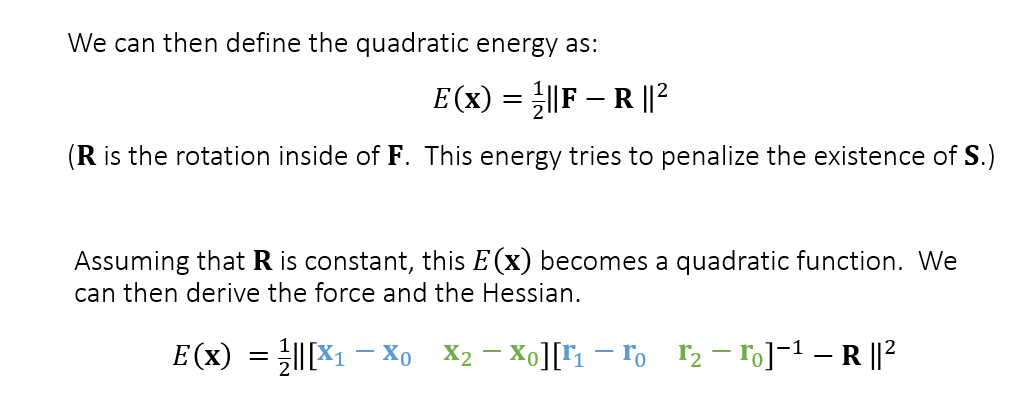GAMES103.王华民.06.Constrained Approaches(PBD, PD and others)

Posted on Edited on In Views:
布料模拟、Bending issue、Locking issue、shape matching 方法

布料模拟

Bending Issue

  • 弯曲问题
  • 在弹簧质点系统中，我们加上一条弯曲边，用于防止布料的弯折

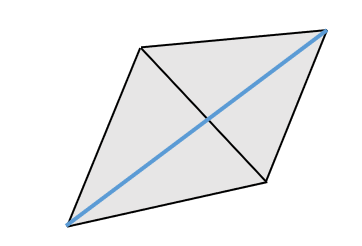
  • 但是当布料平放在桌面上的时候，微小的弯曲导致弹簧的形变也比较小，此时抵抗力比较小，呈现出布料弯曲的样子，这与事实不符

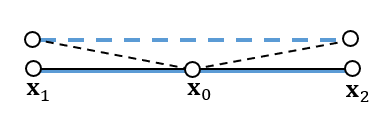
  • 如何构造弯曲的抵抗？
    • 角度：使用两个三角形的夹角来构造抵抗弯曲的力
    • 二面角方法

二面角弯曲模型

  • A Dihedral Angle Model
  • 用于解决 Bending 问题
  • 将弹簧的弯曲力写成二面角的形式

\[ \mathbb{f}_i=f(\theta)\mathbb{u}_i \]

  • \(f(\theta)\)：力的大小
  • \(\mathbb{u}_i\)：力的方向

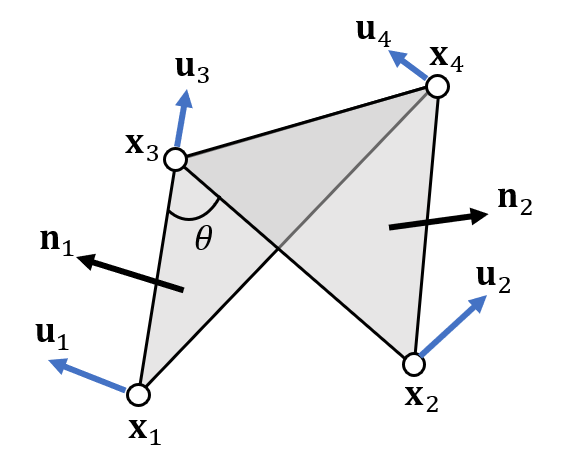
  • 一个二面角涉及到 4 个点

方向

  • \(\mathbb{u}_1,\mathbb{u}_2\) 应该在三角形对应的法向上
  • \(\mathbb{u}_3-\mathbb{u}_4\) 应该和 \(\mathbb{x}_3\mathbb{x}_4\) 这条边垂直
    • 不将这条边进行拉伸
    • 此时 \(\mathbb{u}_3-\mathbb{u}_4\) 是 \(\mathbb{n}_1,\mathbb{n}_2\) 的线性组合
      • 法向都和 \(\mathbb{x}_3\mathbb{x}_4\) 这条边垂直
  • 合力为 \(\mathbb{0}\)
    • \(\Rightarrow\mathbb{u}_3+\mathbb{u}_4\) 是 \(\mathbb{n}_1,\mathbb{n}_2\) 的线性组合
    • \(\Rightarrow\mathbb{u}_3,\mathbb{u}_4\) 是 \(\mathbb{n}_1,\mathbb{n}_2\) 的线性组合
  • 结果如下

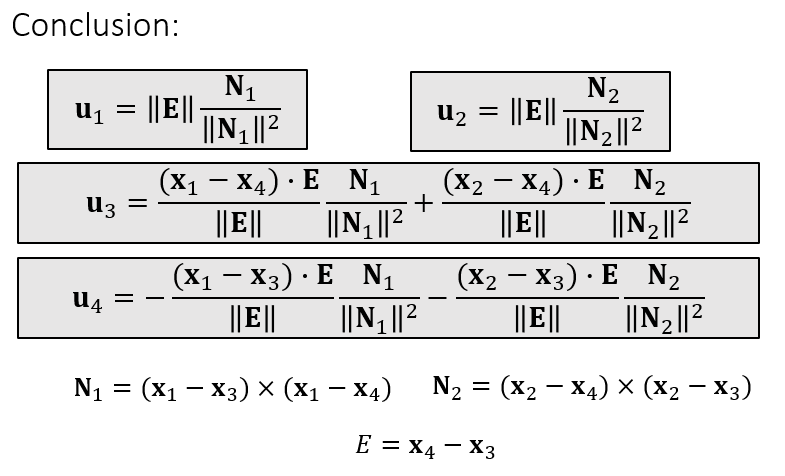
大小

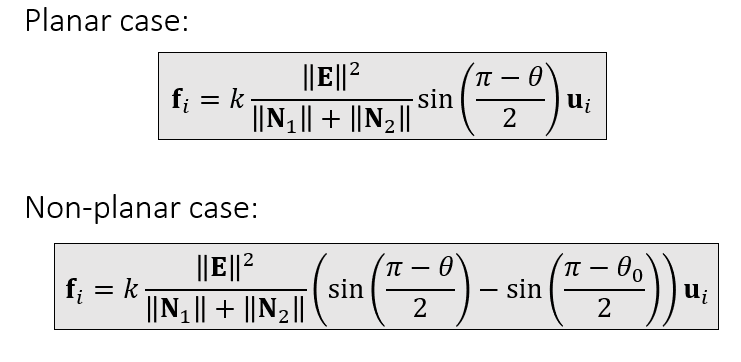
  • planar case：放松的时候是平面的
  • non-planar case：放松的时候有一个夹角 \(\theta_0\)

细节

  • Bridson et al. 2003. Simulation of Clothing with Folds and Wrinkles. SCA.
    • 经典文献
  • 还提到了一些其他问题
    • 自碰撞处理
    • 积分模拟
      • 显示积分
      • 隐式积分：求导非常难算
  • 问题
    • 所有推导都是基于力，没有谈到任何关于能量的信息

二次弯曲模型

  • A Quadratic Bending Model
  • 处理弯曲问题
  • 两个假设
    • 静止放松的时候是平面
    • 没有什么形变（拉伸非常小），只有弯曲导致的形变
  • 根据拉普拉斯变换推导出来如下能量表示形式

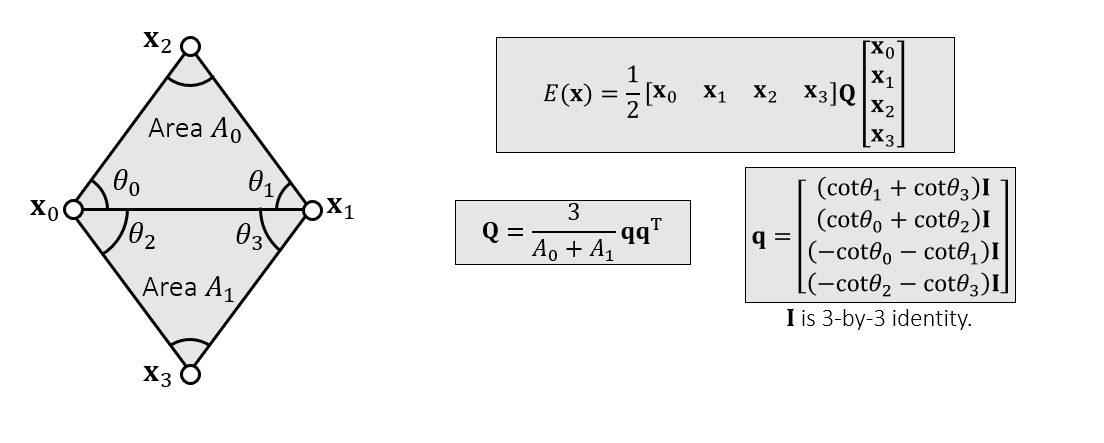
  • \(\mathbb{q}\in\mathbb{R}^{12\times3}\)
  • 表达式变化改写如下

\[ E(\mathbb{x})=\dfrac{3\Vert\mathbb{q}^{\mathbb{T}}\mathbb{x}\Vert^{2}}{2(A_0+A_1)} \]

  • 上面的式子在估算两个三角形的曲率（拉普拉斯）
  • 平的时候，曲率为 0，\(E(\mathbb{x})=0\)
  • 推导是基于数学中曲率的定义推导得到的，而不是物理测量得到的

评价

Pros

  • 二阶的形式，很容易计算力，因此很容易实现

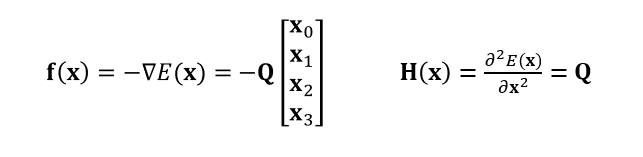
  • 容易使用隐式积分模拟的方式

Cons

  • 拉伸很厉害的话，模拟不再准确
  • 如果两个三角形在静止的时候不是平面的话，模拟不准确
    • 改进：cubic shell model
    • 其他：projective dynamics model

细节

  • Bergou et al. 2006. A Quadratic Bending Model for Inextensible Surfaces. SCA.

Locking Issue

  • 如下图，如果弹簧很难弯曲，此时，右边的方式很难弯曲
    • 原因是我们认为中间的弹簧只能被压缩，不能被弯曲

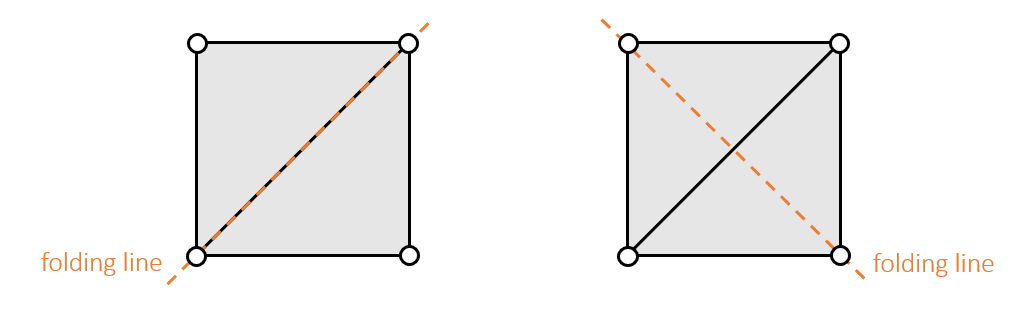
  • 上面的问题就是 locking issue
  • 本质上是由于自由度的丢失导致的
    • DoFs：degrees of freedoms
  • Euler Fomula
    • 对于 manifold mesh，边数 = 3 \(\times\) 顶点数 - 3 - 边缘上的边数
      • #edges=3#vertices-3-#boundary_edges
  • 变量数：3 \(\times\) 顶点数
    • 因此自由度仅仅是 3+#boundary_edges
  • 如果模拟的布是方块形的，自由度更少（边缘上的边更少）
  • 解决方式
    • 弹簧在压缩的时候，弹性系数设置的小一点
    • 弹簧在一定范围内没有力，可以自由伸缩
    • 把自由度定在边上
      • English and Bridson. 2008. Animating Developable Surfaces Using Nonconforming Elements. SIGGRAPH. (optional)
  • 弹簧弹性很弱、网格分辨率很低的时候，locking issue 会很明显
    • 顶点数多了，自由度不变，但是顶点更密会让这种现象缓解（根本问题没有解决）

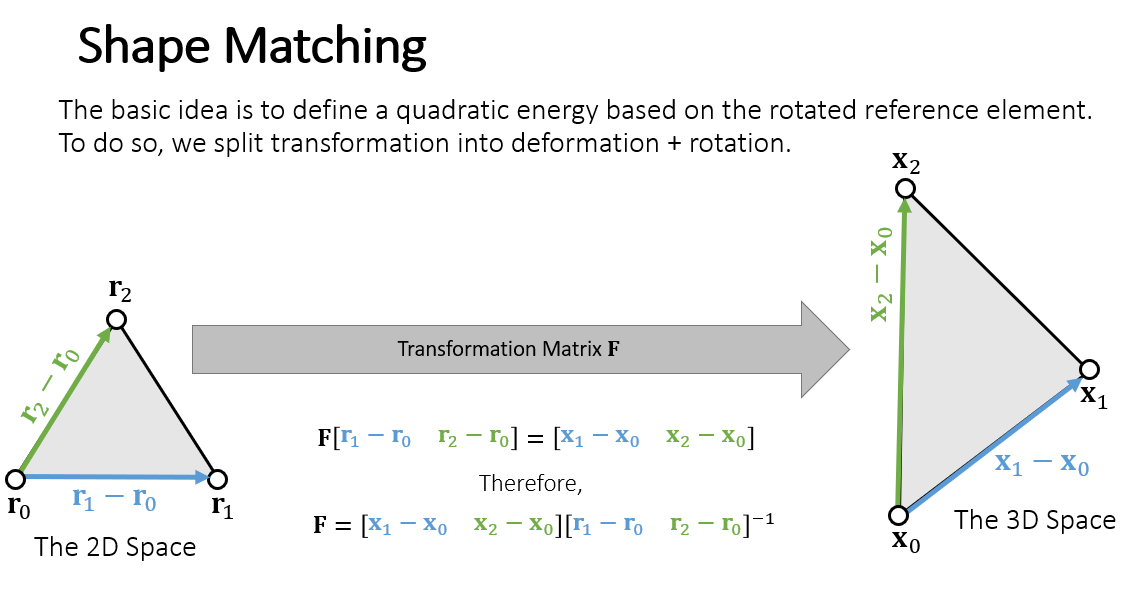
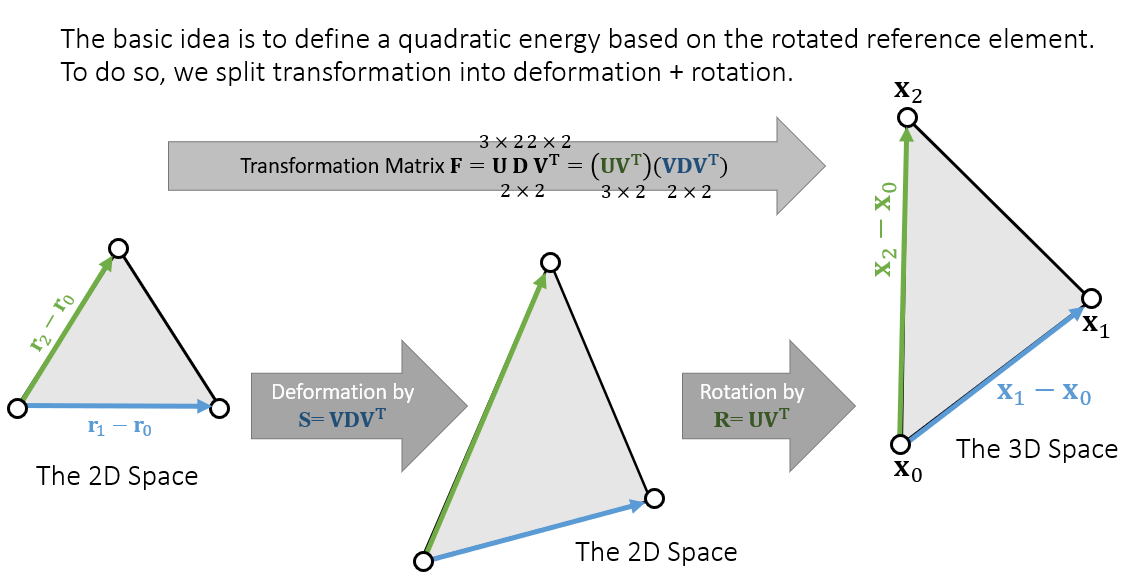
Shape Matching

  • 没讲