GAMES103.王华民.05.Physics-Based Cloth Simulation

Posted on Edited on In Views:
基于物理的布料模拟、弹簧质点系统、显式积分模拟、隐式积分模拟、牛顿法、线性方程组求解

布料模拟

  • 刚体的其他话题
    • Articulation Body
      • 关节体（人体骨骼动画）
  • 方法：物理仿真模拟、基于约束的（PBD）、两者结合

主题

  • 弹簧质点系统（Mass-Spring System）
    • 隐式积分、显式积分
  • 弯曲（bending）、弯曲带来的 locking 问题
  • Co-Rotational Method
    • 类似于 shape matching

弹簧质点系统

  • Mass-Spring System
  • 理想弹簧满足胡克定律
    • Hooke's Law

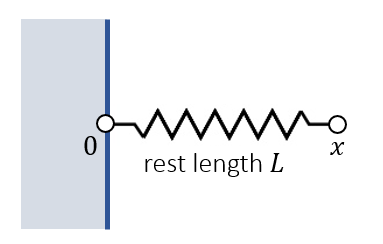
一维

  • 弹簧原长（rest length）\(L\)
  • 能量

\[ E(x)=\dfrac{1}{2}k(x-L)^2 \]

  • 弹簧力：能量对位置的负导数

\[ f(x)=-\dfrac{\mathrm{d}E(x)}{x}=-k(x-L) \]

  • \(k\)：弹性系数（spring stiffness）

二维

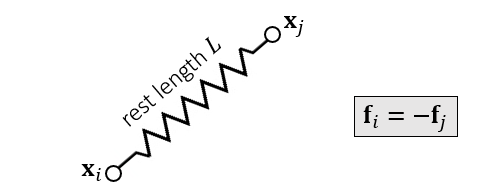
  • 能量

\[ E(\mathbf{x})=\dfrac{1}{2}k(\Vert{\mathbf{x}_i-\mathbf{x}_j}\Vert-L)^2 \]

  • 弹簧力：能量对位置的负梯度
    • 分别对 \(\mathbf{x}_i,\mathbf{x}_j\) 求导

\[ f_i(\mathbf{x})=-\nabla_i E(\mathbf{x})=-k(\Vert{\mathbf{x}_i-\mathbf{x}_j}\Vert-L)\dfrac{\mathbf{x}_i-\mathbf{x}_j}{\Vert{\mathbf{x}_i-\mathbf{x}_j}\Vert} \]

\[ f_j(\mathbf{x})=-\nabla_j E(\mathbf{x})=-k(\Vert{\mathbf{x}_i-\mathbf{x}_j}\Vert-L)\dfrac{\mathbf{x}_j-\mathbf{x}_i}{\Vert{\mathbf{x}_i-\mathbf{x}_j}\Vert} \]

\[ f_j(\mathbf{x})=-f_i(\mathbf{x}) \]

多根弹簧

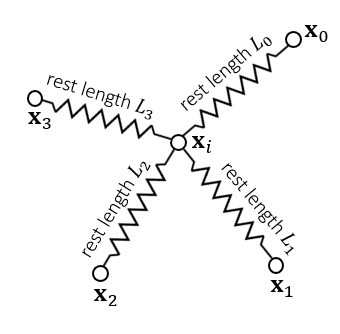
  • 能量和力都是可以叠加的
    • 能量：标量和
    • 力：矢量和

\[ E=\sum_{e=0}^{3}\dfrac{1}{2}k(\Vert{\mathbf{x}_i-\mathbf{x}_e}\Vert-L_e)^2 \]

\[ \mathbf{f}_i=-\nabla_iE=\sum_{e=0}^{3}-k(\Vert{\mathbf{x}_i-\mathbf{x}_e}\Vert-L)\dfrac{\mathbf{x}_i-\mathbf{x}_e}{\Vert{\mathbf{x}_i-\mathbf{x}_e}\Vert} \]

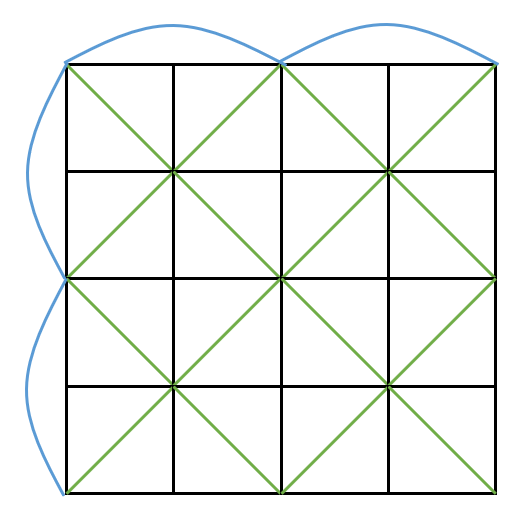
结构化的弹簧网络

  • Structured Spring Networks
  • 弹簧类型
    • Horizontal（水平方向）
    • Vertical（竖直方向）
    • Diagonal（对角的）
    • Bending（弯曲的）
      • 防止面料任意的弯折

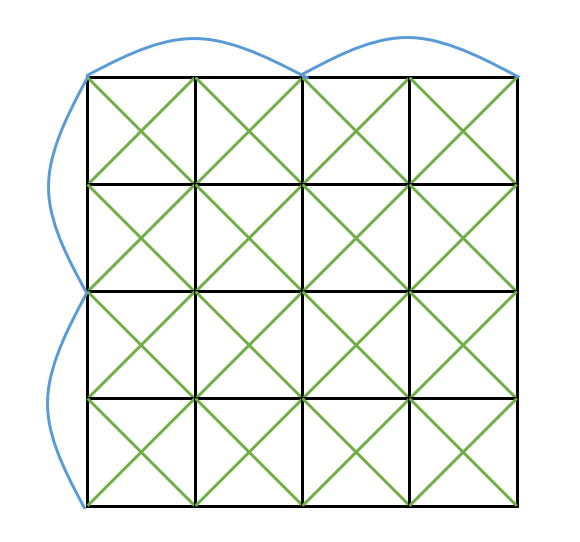
  • 简化的弹簧网络
    • 每一个小单元只保留 45 度或者 135 度的对角弹簧
    • 不能都使用 45 度或者 135 度的，这样会让模拟有偏向性

非结构化的弹簧网络

  • Unstructured Spring Networks
  • 面料不规则的版型
  • 使用三角网格设计
  • 弹簧
    • Edges：每一条边都认为是一条弹簧
    • Bending：相邻的两个三角形的相对的两个顶点加一根弹簧
      • 用于抵抗弯曲

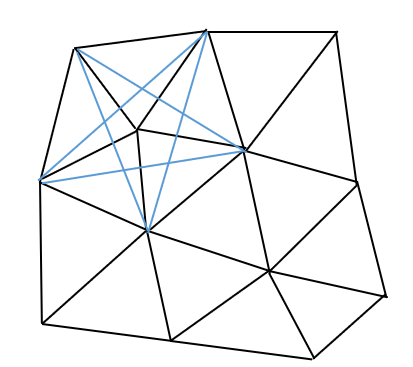
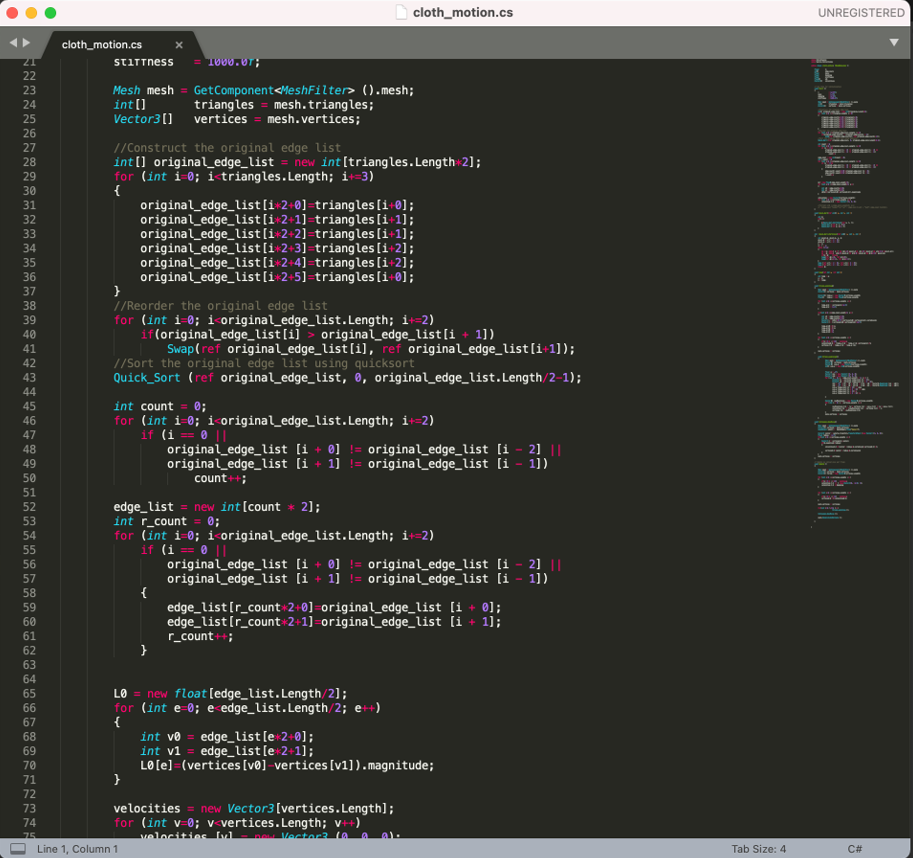
  • 三角网格的表示
    • 顶点列表 + 索引列表

  • 从上面的三角网格中获取到边的信息（表示边）
  • 不能简单的直接把每个三角形的拿出来作为弹簧，因为存在重复边
    • 内部边被两个三角形共享
  • Topological Construction（拓扑结构）
    • 几何处理

表示弹簧边

  • 构造一个三元组列表（Triple list）
    • （顶点1，顶点2，三角形序号）
      • 顶点1 < 顶点2
  • 对这个三元组列表进行排序
    • 排序规则：逐个比较三元组中的元素
    • 排序之后重复的边位置会相邻
  • 去除重复边，与此同时得到弯曲边
    • 重复边：顶点1、2的索引都相同
    • 弯曲边：重复边对应一条弯曲边
      • 可以获取到相邻的两个三角形的信息
      • 检查这两个三角形，获取到 Bending Edge
    • 可以直接保存弯曲边，也可以保存相邻三角形对
  • 算法过程如下

  • 参考代码
    • lab2

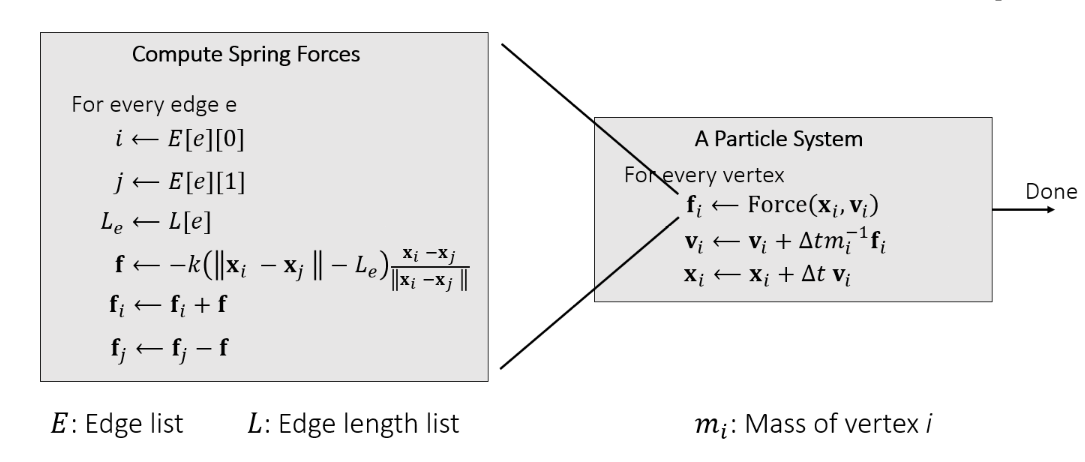
模拟系统（显式积分）

  • Explicit Integration
  • 简单的粒子系统
    • 对于每一个结点，计算他所受到的力
      • 遍历每一根弹簧，把力叠加到结点上
    • 通过力计算加速度
    • 更新速度
    • 更新位置
  • 算法如下
    • 先算所有的力，再更新

显式积分的问题

  • numerical instability（数值上是不稳定的）
  • overshooting 问题
    • 弹簧的弹性系数 \(k\) 非常大 / 时间间隔 \(\Delta t\) 非常小 \(\to\) 力非常大
  • 例子如下
    • 状态1弹簧力非常大 \(\to\) 计算得到状态2
    • 状态2弹簧力更大 \(\to\) 计算得到状态3
    • 状态3弹簧力更大 \(\to\cdots\)

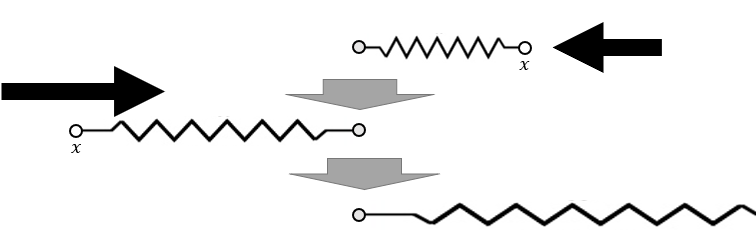
  • 简单的解决方案：使用更小的时间间隔 \(\Delta t\)
    • 让整个数值模拟过程变慢
  • 其他解决方案：隐式积分

模拟系统（隐式积分）

  • \(\mathbf{x}\) 表示所有顶点（\(\mathbb{R}^{3N}\)），\(\mathbf{M}\) 表示每个顶点的质量（对角矩阵）（\(\mathbb{R}^{3N\times3N}\)）

  • 左边
    • 当前时刻是 \([1]\)，我们不知道 \(\mathbf{f}^{[1]}\)
  • 右边
    • 消元 \(\mathbf{v}^{[1]}\)，重写第二个式子
    • 转化为如何求得 \(\mathbf{x}^{[1]}\)
  • 我们做如下假设，\(\mathbf{f}^{[1]}\) 之和位置 \(\mathbf{x}^{[1]}\) 相关（不一定是线性的），此时转化为如下的方程

\[ \mathbf{x}^{[1]}=\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0]}+\Delta t^2\mathbf{M}^{-1}\mathbf{f}(\mathbf{x}^{[1]}) \]

  • 就是计算方法中学的隐式积分
  • 等价于如下的优化问题，\(E(\mathbf{x})\) 是能量的表达式
    • 保守力才能够表示为能量的形式，非保守力不能
    • \(\Vert{\mathbf{x}}\Vert^2_{\mathbf{M}}=\mathbf{x}^{\mathbf{T}}\mathbf{M}\mathbf{x}\)

\[ F(\mathbf{x})=\dfrac{1}{2\Delta t^2}\Vert{\mathbf{x}-\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0]}}\Vert^{2}_{\mathbf{M}}+E(\mathbf{x}) \]

\[ \mathbf{x}^{[1]}=\arg\max{F(\mathbf{x})} \]

  • \(\nabla F(\mathbf{x})=0\) 就是上面的方程
    • \(\mathbf{f}(\mathbf{x})=-\nabla E(\mathbf{x})\)
  • 这个方法不仅仅能够使用在弹簧系统中，也适用于其他系统

牛顿法

  • Newton-Raphson Method
  • 对于优化问题 \(\mathbf{x}^{[1]}=\arg\max{F(\mathbf{x})}\)，要求 \(F(\mathbf{x})\) 是利普希茨连续的（Lipschitz continuous）
  • 一阶泰勒展开

\[ \begin{aligned} 0=F'(x) &\approx F'(x^{(k)})+F''(x^{(k)})(x-x^{(k)})\\ &=F'(x^{(k)})+F''(x^{(k)})\Delta x\\ \end{aligned} \]

  • 牛顿迭代法

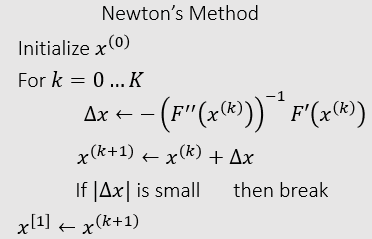
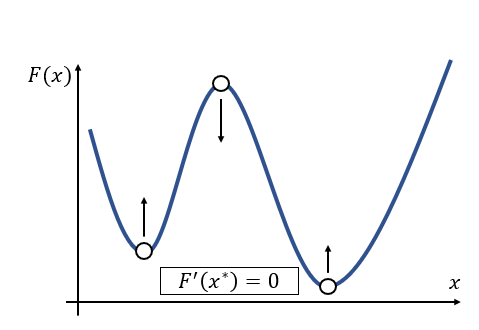
  • 问题
    • 可能会陷入局部最优
      • 随机扰动
    • 找到的可能是极大值或者极小值
      • 如果二阶导恒大于等于 0，没有极大值，存在唯一的极小值

高维牛顿法

\[ \begin{aligned} \mathbf{0}=\nabla F(\mathbf{x}) &\approx \nabla F(\mathbf{x}^{(k)})+\dfrac{\partial F^{2}(\mathbf{x}^{(k)})}{\partial \mathbf{x}^2}(\mathbf{x}-\mathbf{x}^{(k)})\\ &= \nabla F(\mathbf{x}^{(k)})+\dfrac{\partial F^{2}(\mathbf{x}^{(k)})}{\partial \mathbf{x}^2}\Delta\mathbf{x}\\ \end{aligned} \]

  • 一阶导数是一个向量，二阶导数是一个矩阵
  • 算法

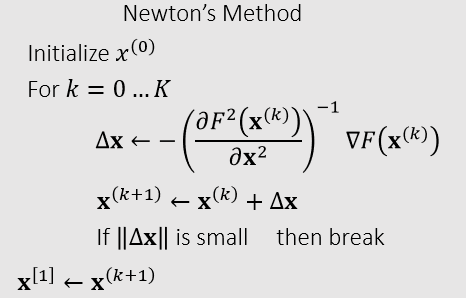
牛顿法求解上述问题

\[ F(\mathbf{x})=\dfrac{1}{2\Delta t^2}\Vert{\mathbf{x}-\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0]}}\Vert^{2}_{\mathbf{M}}+E(\mathbf{x}) \]

  • 在方法中的参数如下

\[ \nabla F(\mathbf{x}^{(k)})=\dfrac{1}{\Delta t^2}\mathbf{M}\left({\mathbf{x}^{(k)}-\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0]}}\right)-\mathbf{f}(\mathbf{x}^{(k)}) \]

\[ \dfrac{\partial F^{2}(\mathbf{x}^{(k)})}{\partial \mathbf{x}^2} =\dfrac{1}{\Delta t^2}\mathbf{M}+\mathbf{H}(\mathbf{x}^{(k)}) \]

  • 算法如下

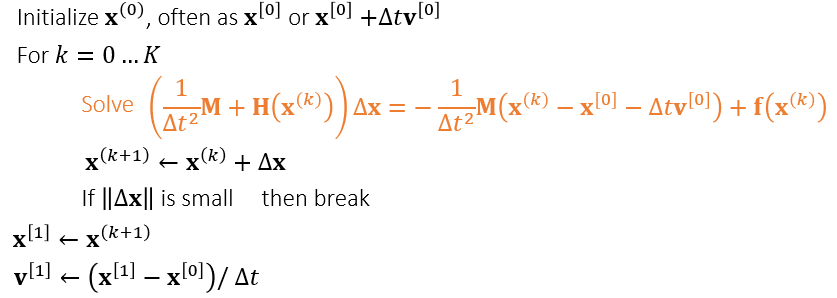
  • 黄色部分：求解线性系统 \(\mathbf{A}\Delta\mathbf{x}=\mathbf{b}\)
    • 之前比较老的方法就是求解一次线性方程组，得到近似结果
    • 牛顿法是多次求解，直到满足容差
  • 还有一个问题，如何求解上面的 Hessian 矩阵 \(\mathbf{H}(\mathbf{x}^{(k)})\) ?

Spring Hessian

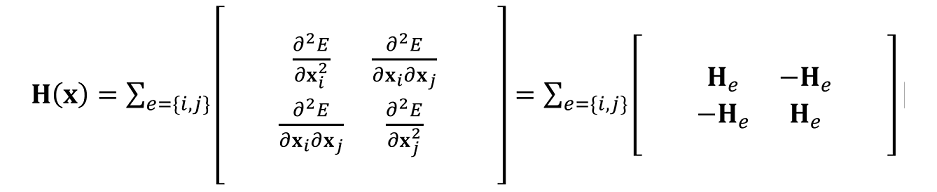
  • \(\mathbf{x}_{ij}=\mathbf{x}_i-\mathbf{x}_j\)

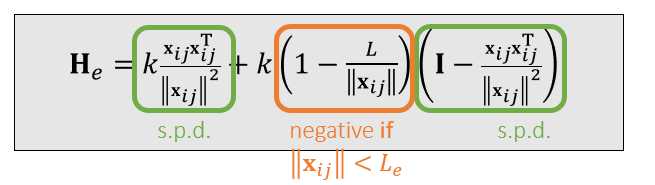
  • 绿色是 s.p.d.（半正定的）
    • \(\mathbf{x}^{\mathbf{T}}\mathbf{V}\mathbf{x}\ge0\)
    • 右边：柯西不等式

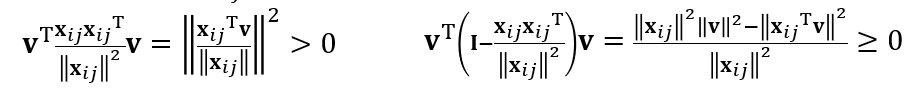
  • 如果黄色部分大于等于 0（弹簧被拉伸），则 \(\mathbf{H}_e\) 是半正定的，因此 \(\mathbf{H}(\mathbf{x})\) 也是半正定的
    • 拉伸的时候，整个系统会更加稳定
  • 黄色部分小于 0（弹簧被压缩），可能是不正定的
  • 整个参数

\[ \dfrac{\partial F^{2}(\mathbf{x}^{(k)})}{\partial \mathbf{x}^2} =\dfrac{1}{\Delta t^2}\mathbf{M}+\mathbf{H}(\mathbf{x}^{(k)}) \]

  • 如果 Spring Hessian 是半正定的，那么函数存在唯一解，是极小值
    • \(\Delta t\) 越小，越正定

压缩弹簧多解的例子

  • 弹簧受挤压，可能会有多种状态
  • 2D：向上或者向下

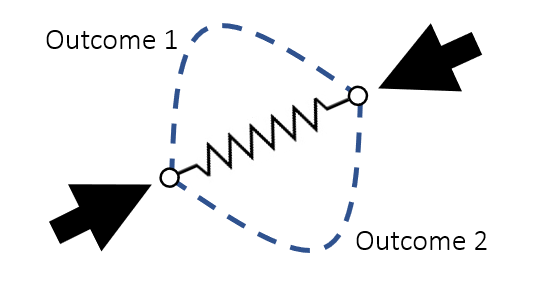
  • 1D 没有这个问题，\(k>0\)
  • 2D、3D 会有这个问题

正定性

  • 正定与否可能会影响某些算法的稳定性
  • 某些算法可能只适用于正定矩阵
  • 保证正定：在检测到弹簧是压缩状态的时候，直接舍去后面一项
    • 比较粗暴的方法（近似）
  • 其他方法
    • Choi and Ko. 2002. Stable But Responive Cloth. TOG (SIGGRAPH)

解线性方程组

  • \(\mathbf{A}\Delta\mathbf{x}=\mathbf{b}\)

直接求解

  • 方法
    • LU 分解、LDLT 分解、Cholesky 分解
  • 代价高，得到精确解
  • 对矩阵 \(\mathbf{A}\) 限制少
  • 适合 CPU 计算

迭代求解

  • 如果需要得到精确解的话代价大，但是可以根据容差控制
  • 要让方法收敛的话，对矩阵 \(\mathbf{A}\) 有比较严格的限制（例如正定）
  • CPU、GPU 都行
  • 实现比较容易
  • 有很多加速算法

雅各比方法

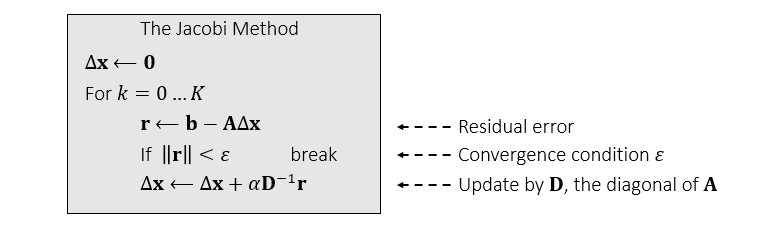
  • 传统的雅各比方法：\(\alpha=1\)
    • 如果矩阵式对角占优的（diagonal dominant），那么能够保证收敛到唯一解
  • 控制 \(\alpha\) 的值，让更多情况下都尽可能收敛到解

切比雪夫加速的雅各比方法

课后阅读

  • Baraff and Witkin. 1998. Large Step in Cloth Simulation. SIGGRAPH.
    • 最早使用隐式积分左布料模拟
    • 将非线性方程线性化，等价于做了一次牛顿迭代