有向距离场(Raymarching SDFs)

Posted on 2022-01-14 Edited on 2022-01-26 In CG.Algorithm Views:

有向距离场（SDF）、RayMarching、AO、软阴影、凹凸贴图

Raymarching SDFs

说明

功能实现

实现了有向距离场上的软阴影（Soft Shadow）、环境光遮蔽（AO）、凹凸贴图（bump mapping）
学习两个经典场景的写法
- 加入了光源、相机位置控制
搭建了一个场景
- 视频
- shadertoy

项目来源

项目来源如下
- Rendering Worlds with Two Triangles with raytracing on the GPU in 4096 bytes
作者使用两个三角形作为输入，不使用图片作为输入，仅使用 4K 资源就渲染出了如下的图片，属实让人震惊
使用有向距离场上的 ray marching 实现的

我也想学习一下有向距离场（SDF）在渲染中的作用，同时也想学习使用 SDF 构造一个自己的场景

概念

SDF

SDF
- signed distance field
- 有向距离场
表示空间中的每一个点到物体表面的最小距离
- 外部为正、内部为负

Ray Marching

光线步进算法，用于和物体求交
对于某一个点，如果他到物体表面的距离（SDF 函数的值）为 \(R\)，则光线前进 \(R\) 一定不会和物体相交
- 利用这个性质实现光线和物体求交的加速

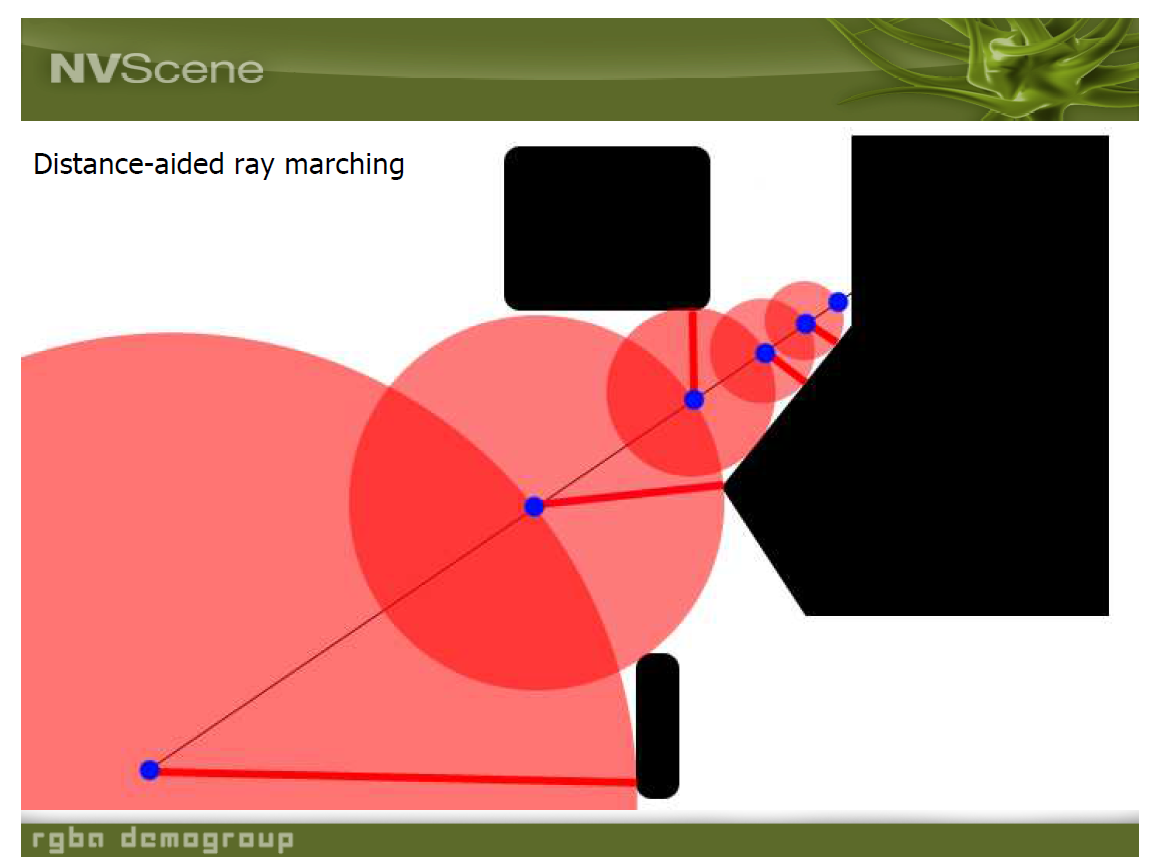
复现

原始作者给出了原始工程在 shadertoy 上的实现，首先我将其移植到 OpenGL 上，实现原始的效果

移植

单纯的移植代码比较简单

shader toy

shader toy 上相当于一个简单的 fragment shader，有如下固定输入

uniform vec3      iResolution;           // viewport resolution (in pixels)
uniform float     iTime;                 // shader playback time (in seconds)
uniform float     iTimeDelta;            // render time (in seconds)
uniform int       iFrame;                // shader playback frame
uniform float     iChannelTime[4];       // channel playback time (in seconds)
uniform vec3      iChannelResolution[4]; // channel resolution (in pixels)
uniform vec4      iMouse;                // mouse pixel coords. xy: current (if MLB down), zw: click
uniform samplerXX iChannel0..3;          // input channel. XX = 2D/Cube
uniform vec4      iDate;                 // (year, month, day, time in seconds)
uniform float     iSampleRate;           // sound sample rate (i.e., 44100)

主函数如下

1
2
3

void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
    // ...
}

移植到 OpenGL

CPU 端程序
- 使用 shader 绘制两个三角形（也就是平面）
- 传入在 shadertoy 中使用的基本参数（被使用到的上面的参数）
vertex shader
- 不需要做任何事，设置位置即可

#version 330 core
layout (location = 0) in vec3 aPos;

void main() {
    gl_Position = vec4(aPos, 1.0);
}

fragment shader

使用 shader toy 中的程序
- 需要修改 mainImage 为 main()
增加输入输出
- 输入：使用到的参数
- 输出：颜色

// 输入
uniform vec3      iResolution;           // viewport resolution (in pixels)
uniform float     iTime;                 // shader playback time (in seconds)
uniform int       iFrame;                // shader playback frame
uniform vec4      iMouse;                // mouse pixel coords. xy: current (if MLB down), zw: click

// 输出
out vec4 FragColor;

fragCoord 修改为 gl_FragCoord

学习代码与重构

示例

(1) 设置相机位置

在 fragment shader 中，我们获取到的是以以相机为观察中心的观察坐标系
通过矩阵（视点坐标系 \(\to\) 世界坐标系）将其变换回世界坐标系中，可以通过 camera 的三个坐标进行构造
是正交变换，而 OpenGL 恰好是列放置的

struct Camera {
    vec3 position;
    vec3 front;
    vec3 up;
    float right;
};

(2) 生成光线

OpenGL 中 fragment shader 中的内置变量 gl_FragCoord 记录了当前像素的中心位置
- 偏移了 (0.5,0.5)
- 范围为 [0.5, w-0.5] * [0.5, h-0.5]
生成的光线用于 ray marching 算法，在函数 raycast() 中实现
生成两条另外的光线，x+1,y+1 两条光线，用于实现其他效果

(3) ray marching

raycast() 函数中，首先和整个场景的包围盒求交，计算出时间的上下界 [tmin, tmax]
map() 函数计算出 sdf 的值
主要步进算法如下

tmin = max(tb.x, tmin);
tmax = min(tb.y, tmax);

// ray marching, 迭代步数为 70
float t = tmin;
for(int i = 0; i < 70 && t < tmax; i++) {
    vec2 h = map(ro + rd*t);
    if(abs(h.x) < (0.0001*t)) {
        res = vec2(t, h.y);
        break;
    }
    t += h.x;
}

map 中计算当前点的 sdf 的值
作者提供了很多原始的图元形式
- 基本图元
- 其他图元

具体的实现部分查看代码注释
返回一个二维向量 vec2 res
- res.x：sdf 的值
- res.y：一个随机数，用于生成物体的颜色

(4) 计算 normal

教程
法线的方向就是 sdf 标量场的梯度方向

\[ n=\textbf{normalize}(\nabla{f(p)}) \]

对于其中的一个维度
前向差分

\[ \dfrac{\mathrm{d}f(p)}{\mathrm{d}x}\approx\dfrac{f(p+(h,0,0))}{h} \]

或者中心差分
- 不会引入方向性的偏差

\[ \dfrac{\mathrm{d}f(p)}{\mathrm{d}x}\approx\dfrac{f(p+(h,0,0))-f(p-(h,0,0))}{2h} \]

中心差分的实现

vec3 calcNormal( in vec3 p ) {
    const float eps = 0.0001; // or some other value
    const vec2 h = vec2(eps,0);
    return normalize( vec3(f(p+h.xyy) - f(p-h.xyy),
                           f(p+h.yxy) - f(p-h.yxy),
                           f(p+h.yyx) - f(p-h.yyx) ) );
}

中心差分的优化形式

vec3 calcNormal( in vec3 & p ) {
    const float h = 0.0001; // replace by an appropriate value
    const vec2 k = vec2(1,-1);
    return normalize( k.xyy*f( p + k.xyy*h ) +
                      k.yyx*f( p + k.yyx*h ) +
                      k.yxy*f( p + k.yxy*h ) +
                      k.xxx*f( p + k.xxx*h ) );
}

推导
- 4 个点：\(k_i=\{1,-1,-1\},\{-1,-1,1\},\{-1,1,-1\},\{1,1,1\}\)
  - \(\sum_{i}k_i=\mathbf{0}\)
- \(\ast\) 表示点对点乘法

\[ \begin{aligned} m&=\sum_{i}k_i\ast f(p+k_ih)\\ &=\sum_{i}k_i\ast(f(p+k_ih)-f(p))\\ &=\sum_{i}k_i\ast(k_ih\ast\nabla{f(p))}\\ &=\sum_{i}4h(\nabla{f(p)})\\ \end{aligned} \]

(5) 光照模型

材质：地面使用经过 filter 的棋盘格，其他使用不同的物体自带的随机数返回一种颜色
光照模型使用 Blinn-Phong 模型
天空盒、直接光源

(6) AO

环境光遮蔽的计算

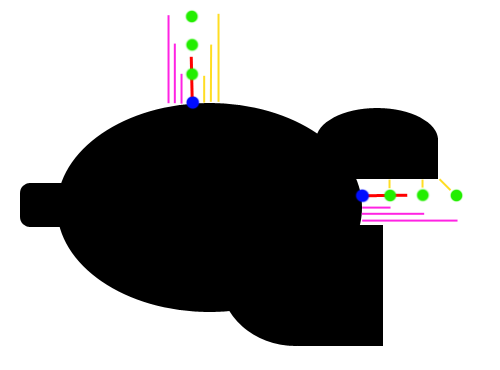
思路
- 在着色点 p 的周围采样若干个点，计算它们的 sdf 值，和到 p 点的距离作比较
- 上面的粉红色和黄色的值相差越大，说明周围遮蔽越严重

\[ \begin{aligned} ao &=1-k\sum_{i=1}^{5}\dfrac{1}{2^i}(\textrm{pink}_i-\textrm{yellow}_i)\\ &=1-k\sum_{i=1}^{5}\dfrac{1}{2^i}(i\cdot\Delta-\mathrm{sdf}(p+n\cdot i\cdot\Delta))\\ \end{aligned} \]

(7) 软阴影

教程

硬阴影

向着光源的方向步进，如果碰到物体则在阴影中，没有则不在阴影中

float t = mint;
for(int i = ZERO; i < 24; i++) {
    float h = map( ro + rd*t ).x;
    if(h < 0.0001) return 0.0;
    t += h;
}
return 1.0;

软阴影

当向着光源的方向步进的时候没有碰到物体，但是离物体很近的时候，这时候对阴影也是有贡献的
两个观察，点 \(p\) 离物体很近
- \(p\) 离着色点越近，则阴影越硬
- \(p\) 离物体越近（sdf 值越小），则阴影越硬

const float k = 10.0; // k 是一个可调参数, 越小阴影越软(弥散越开)

float res = 1.0;
float t = mint;
for(int i = ZERO; i < 24; i++) {
    float h = map( ro + rd*t ).x;
    if(h < 0.0001) return 0.0;
    res = min(res, k*h/t);
    t += h;
}
return res;

软阴影（改进）

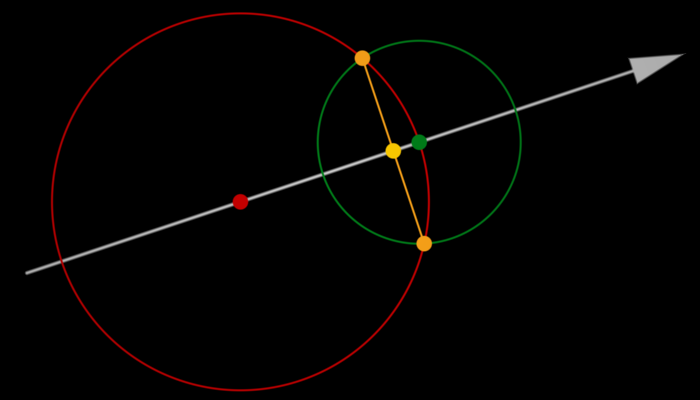
我们在步进的时候可能错过产生最硬的阴影的点（例如图上的黄点），引入的问题就是会造成漏光现象（light leaking）
解决方案就是试图求出黄色的点对应的步进长度
红色圆的半径 \(r_1\)，绿圆半径 \(r_2\)，则实际上的到物体表面的距离（黄线的一半）如下

\[ r_2\cos\theta=r_2\sqrt{1-\left(\dfrac{r_2/2}{r_1}\right)^2} \]

float k = 10.0; // k 是一个可调参数, 越小阴影越软(弥散越开)

float res = 1.0;
float t = mint;

float ph = 1e20;
for(int i = ZERO; i < 24; i++) {
    float h = map( ro + rd*t ).x;
    if(h < 0.0001) return 0.0;
    float y = h*h/(2.0*ph);
    float d = sqrt(h*h - y*y);
    res = min(res, k*d/max(t - y, 0.0));
    ph = h;
    t += h;
}
return res;

其他问题，将阴影估计深了，例如下方黄线为物体包络线

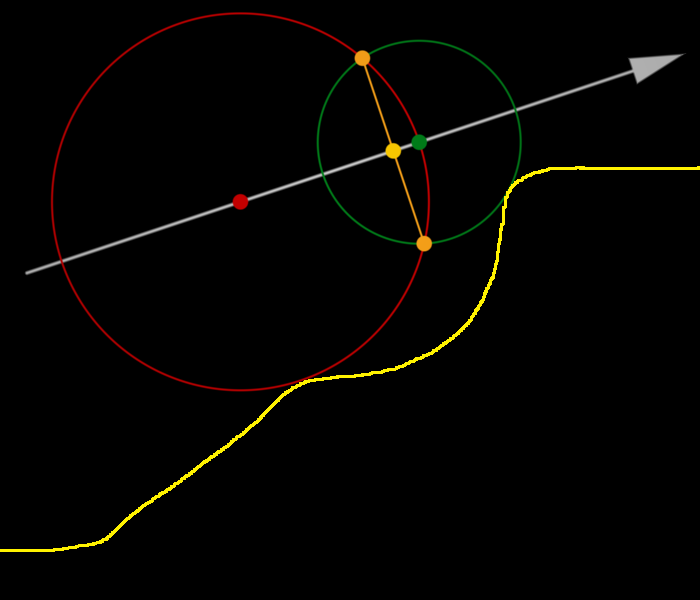
问题不大，因为之后确实有这么深的阴影（第二个接触点）
改进前后对比
其他问题：左下角的这些残影？
- 上面的方法是没有的

另一种实现

shadertoy 是这么写的
这种方式是没有残影的
就是没改进的软阴影，但是改进了 \(t,d\) 的函数
限制了步进的长度，从而减小漏光情况的发生

float res = 1.0;
float t = mint;
for(int i = ZERO; i < 24; i++) {
    float h = map( ro + rd*t ).x;
    // 就是最简单的 softshadow(没有改进)
    // k=8.0
    float s = clamp(8.0*h/t, 0.0, 1.0);
    res = min( res, s );
    // t += clamp( h, 0.02, 0.2 );
    t += h;
    if( res < 0.037 || t > tmax ) break;
}
res = res*res*(3.0 - 2.0*res); // 0.037 => 0.004
return clamp( res, 0.0, 1.0 );

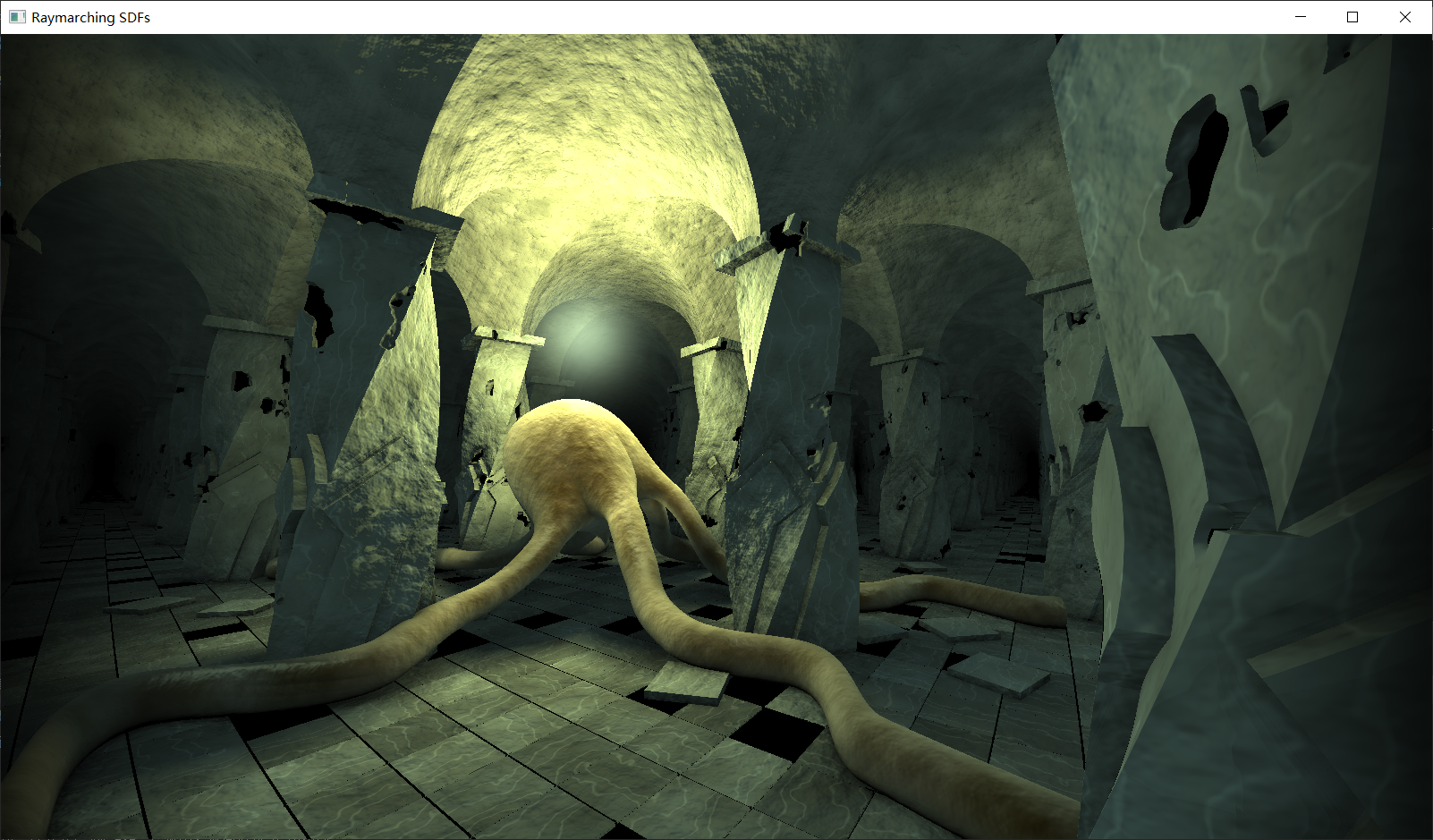
(8) 结果

monstor 场景实现

基本思路同上面相同，其他技术细节写在下面

(1) 场景搭建

柱子

sdf 函数中对应的部分如下

章鱼哥

见代码注释

(2) bump mapping

对法线进行随机扰动

(3) 光源的雾状效果

如果距离光源足够近，则叠加上一层光源的颜色

// 光源
{
    vec3 v1 = lightPositionOffset + LIGHT_POSITION - camera.position;
    float lig_dist2 = dot(v1, v1);
    float dist = dot(v1 ,rd);
    float seg2 = lig_dist2 - dist*dist;
    #if 1
    // 叠加雾状光源
    // (1) 光源在物体前面 / 没有击中物体
    if((dist > 0 && (dist < t || matID == 666u))) {
        col += vec3( 1.0, 0.95, 0.90 )*0.75*exp2( -64.0*seg2 );
    }
    #else
    // 击中光源直接返回
    #define R2 0.01
        // (1) 光源在物体前面 / 没有击中物体
        // (2) 击中光源
        if((dist > 0 && (dist < t || matID == 666u)) && (seg2 < R2)) {
            return vec3( 1.0, 0.95, 0.90 );
        }
    #endif
}

(4) 结果展示

新场景搭建

茶杯、走路的小人、两本书、苹果

参考资料

参考图
SDF 任务
- https://weirdmachine.me/proj5-distancefields/
- https://weirdmachine.me/proj5-distancefields/proposal/index.html
SDF 的一些视频教程
- Box Function