计算方法B.裴玉茹.09.常微分方程(5)

Posted on Edited on In Views:
常微分方程初值问题、欧拉方法、高阶泰勒方法、龙格库塔方法、可变步长方法、多步方法
  • PPT（常微分方程）

常微分方程

  • 这里的局部截断误差都使用 PPT 的定义好了（需要除以步长 \(h\) ）

1. 引子

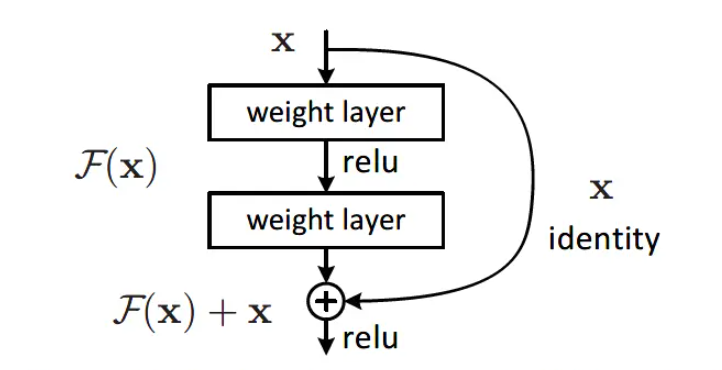
神经 ODE

  • 残差网络跳连

\[ h_{l+1}=h_{l}+\textrm{NNetwork}(h_l) \]

  • ODE 前向欧拉方法

\[ h_{N}=h_{N-1}+\Delta tg((N-1)\Delta t,h_{N-1}) \]

  • 神经 ODE
    • 把跳连使用 ODE 替换

\[ \begin{aligned} h_{t+1}&=h_{t}+f(h_t,\theta_t)\\ \dfrac{\mathrm{d}h(t)}{\mathrm{d}t}&=f(h(t),t,\theta) \end{aligned} \]

2. 常微分方程初值问题

  • IVP：initial value problem

利普希茨条件

  • Lipschitz 条件
  • 凸集
  • 初值问题的唯一解定理
    • 利普希茨连续条件

恰定问题

  • well-posed

  • 如果初值问题 \(\dfrac{\mathrm{d}y}{\mathrm{d}t}=f(t,y),t\in[a,b],y(a)=\alpha\) 满足如下两个条件，则是一个恰定问题

    1. 存在唯一解 \(y(t)\)
    1. 对于任意 \(\epsilon\)，存在正常数 \(\vert\epsilon_0\vert<\epsilon\)，满足 \(\delta(t)\le\epsilon\)，在 \([a,b]\) 上连续，有如下问题的唯一解 \(z(t)\) \[ \dfrac{\mathrm{d}z}{\mathrm{d}t}=f(t,z)+\delta(t),t\in[a,b],z(a)=\alpha+\epsilon_0 \]
    • 存在 \(k>0\)，\(\vert{z(t)-y(t)}\vert<k\epsilon\)，\(t\in[a,b]\)

  • 条件 (2) 的含义就是，初始值有误差，计算有误差，结果的误差不至于太大（线性）

3. 欧拉方法

\[ \begin{aligned} w_0&=\alpha\\ w_{i+1}&=w_i+hf(t_i,w_i),\quad i\in\N\\ \end{aligned} \]

  • 二阶
  • 示例图

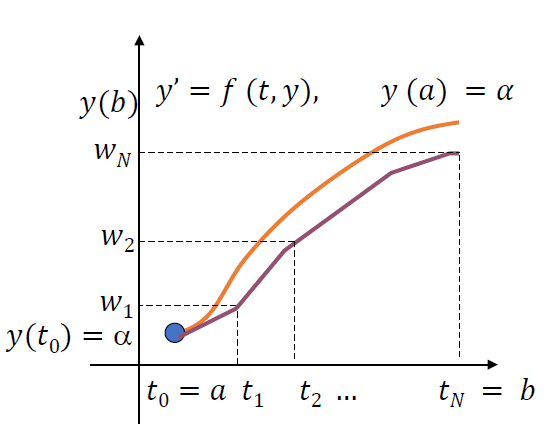
误差证明

  • 教材上的证明是通过局部截断误差来得到全局截断误差
  • PPT 上的方法如下

引理1

\[ \forall x\ge-1,\forall m>0\Longrightarrow0\le(1+x)^m\le e^{mx} \]

  • 泰勒展开

\[ \begin{array}{c} e^{x}=1+x+\dfrac{1}{2}x^2e^{\xi}\ge1+x\ge0\\ (e^x)^{m}\ge(x+1)^{m}\ge0\\ \end{array} \]

引理2

  • 正实数 \(s,t\)，序列 \(\{a_i\}_{i=0}^{k}\) 满足 \(a_0\ge-\dfrac{t}{s}\)，\(a_{i+1}\le (1+s)a_i+t\)，则有

\[ a_{i+1}\le e^{(i+1)s}(a_0+\dfrac{t}{s})-\dfrac{t}{s} \]

  • 一步步代入即可证明

\[ \begin{aligned} a_{i+1}&\le(1+s)a_i+t\\ &\le(1+s)^2a_{i-1}+t(1+(1+s))\\ &\cdots\\ &\le(1+s)^{i+1}a_0+t\dfrac{(1+s)^{i+1}-1}{s}\\ &=(1+s)^{i+1}\left(a_0+\dfrac{t}{s}\right)-\dfrac{t}{s}\\ &\le e^{(i+1)s}(a_0+\dfrac{t}{s})-\dfrac{t}{s} \end{aligned} \]

欧拉方法误差界

  • 利普希茨常数 \(L\)，\(\vert{y''}\vert\le M\)

\[ \vert{y(t_i)-w_i}\vert\le\dfrac{hM}{2L}(e^{(t_i-a)L}-1) \]

  • 泰勒展开

  • 使用引理 2 即可

确定步长

  • 综合考虑截断误差与舍入误差
    • 认为 \(\delta_i<\delta\)

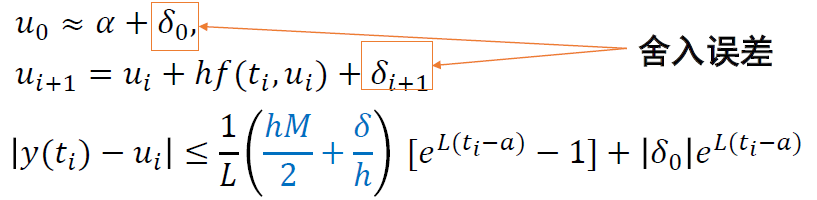
4. 高阶泰勒方法

  • \(n\) 阶泰勒方法，把 \(y\) 展开到 \(n\) 阶，误差为 \(n+1\) 阶
    • 即 \(f(t,y)\) 展开到 \(n-1\) 阶
  • 定义如下

\[ \begin{aligned} w_0&\approx{\alpha}\\ w_{i+1}&=w_i+hT^{(n)}(t_i,w_i) \end{aligned} \]

  • 其中 \(T^{(n)}(t,y)\) 定义如下

\[ T^{(n)}(t,y)=f(t,y)+\dfrac{h}{2}f'(t,y)+\dfrac{h^2}{6}f''(t,y)+\cdots+\dfrac{h^{n-1}}{n!}f^{n-1}(t,y) \]

  • 带入上面的式子，可以发现其实就是把 \(y(t_{i+1})\) 在 \(t_i\) 处进行了 \(n\) 阶泰勒展开

局部截断误差(书本)

  • 书上的定义
  • \(n\) 阶泰勒公式
    • \(n\) 阶 \(\Rightarrow\) \(n+1\) 阶局部截断误差 \(\Rightarrow\) \(n\) 阶全局误差

局部截断误差(PPT)

\[ \begin{aligned} w_0&\approx{\alpha}\\ w_{i+1}&=w_i+h\phi(t_i,w_i) \end{aligned} \]

  • 按照 PPT 上的定义，局部截断误差定义如下
    • 和书上相比除了一个 \(h\)

\[ \tau_{i+1}(h)=\dfrac{y_{i+1}-(y_i+h\phi(t_i,w_i))}{h}=\dfrac{y_{i+1}-y_i}{h}-\phi(t_i,w_i) \]

  • 如此定义的话
    • \(n\) 阶 \(\Rightarrow\) \(n\) 阶局部误差 \(\Rightarrow\) \(n\) 阶全局误差

5. 插值

  • 除了等间距格点上的函数值，其它位置的函数值如何计算？
    • 插值
  • 线性插值、Hermit 插值

6. Runge-Kutta方法

  • 具有高阶泰勒方法的局部截断误差
  • 无需计算函数 \(f(t,y)\) 的导数

二维泰勒展开

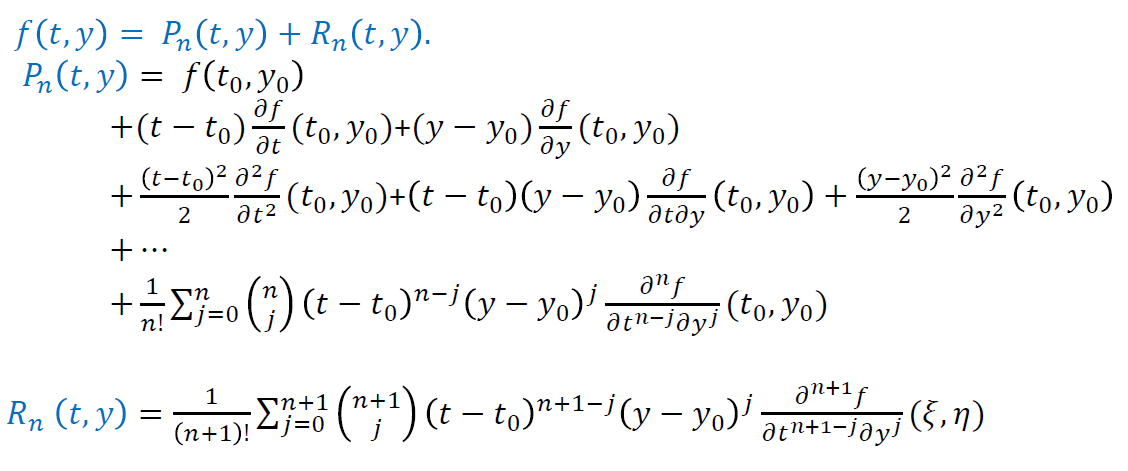
RK2

  • 如何构造 k 阶龙格库塔方法？
  • 例如 RK2，局部截断误差 \(O(h^2)\)
    • PPT 定义（除以 \(h\) 后）
  • 但是外面会乘一个 \(h\)，只需要将 \(f(t,y)\) 二阶展开
    • 因为是对斜率进行估计
  • 引入如下函数，使其与二阶泰勒公式 \(T^{2}(t,y)\) 一致

\[ a_1f(t+\alpha_1,y+\beta_1) \]

  • 对应项系数相等

RK3

  • \(T^{3}(t,y)\) 展开

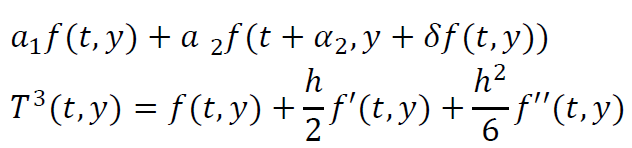
  • 改进欧拉方法

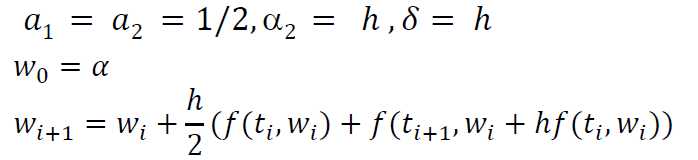
  • Heun 方法

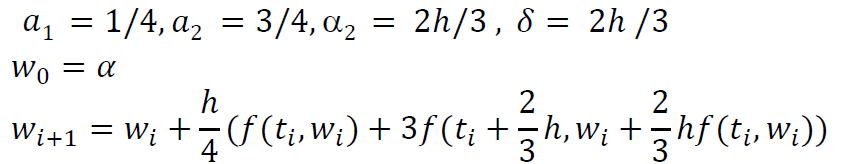
RK4

同伦与延拓方法

  • 求解方程组的解转化为 ODE 的初值问题

龙格库塔方法

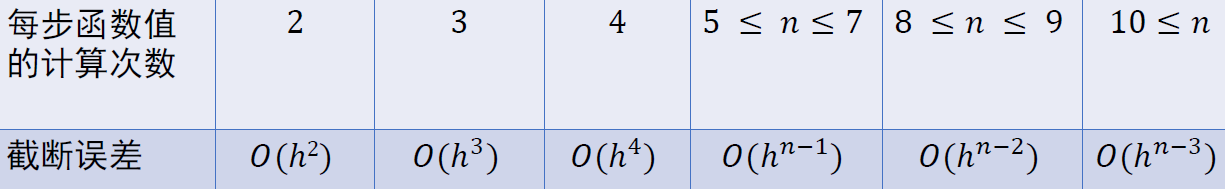
  • 计算代价包含每步中函数值的计算

7. 可变步长方法

Runge-Kutta-Fehlberg 方法

  • 利用 \((n+1)\) 阶方法作为真值评估误差
  • 记号

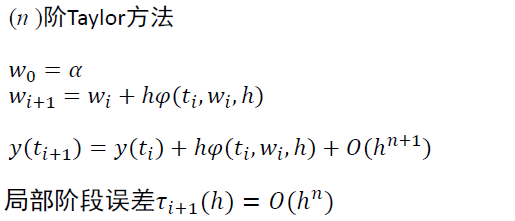
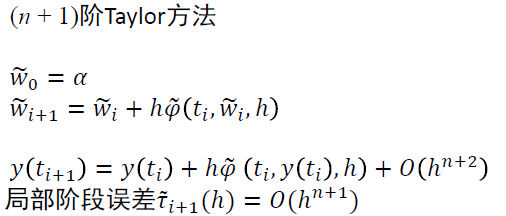
  • 估计局部截断误差，认为 \(w_i=y(t_i)=\tilde{w}_i\)

\[ \tau_{i+1}(h)=\dfrac{y(t_{i+1})-y(t_{i})}{h}-\phi(t_i,y(t_i),h)=\dfrac{y(t_{i+1})-w_{i+1}}{h} \]

\[ \tilde{\tau}_{i+1}(h)=\dfrac{y(t_{i+1})-\tilde{w}_{i+1}}{h} \]

  • 估计误差
    • \(q\) 为步长修正系数（要求如何选择步长）
    • 这里使用绝对误差 \(\epsilon\)

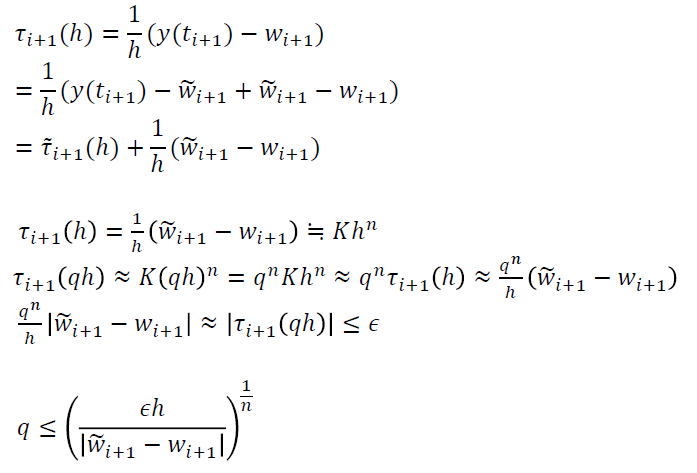
  • 对比
    • RK 4/5：共需要10（4+6）次函数值计算
    • RKF 4/5：共需要 6 次函数值计算

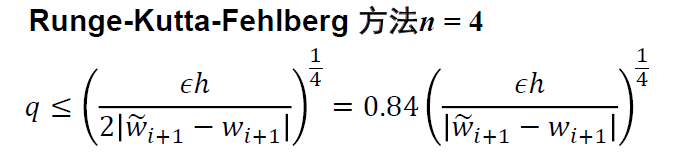
  • 修正步长
    • \(q<1\)：说明需要减小步长，之前的计算超出了要求的误差界
      • 因此需要拒绝 \(h\)，加大步长值重新计算
    • \(q\ge1\)：接受当前步的计算，为下一步设置合适的 \(h\)

8. 多步方法

  • 显式方法、隐式方法
    • \(b_m{\buildrel\rm{?}\over=}0\)（PPT 定义和书上顺序反一下）

插值多项式近似

\[ y(t_{i+1})-y(t_i)=\int_{t_i}^{t_{i+1}}f(t,y)\;\mathrm{d}t\approx\int_{t_i}^{t_{i+1}}P(y)\;\mathrm{d}t \]

构造多步方法

Adams 方法

后向欧拉方法

  • 隐式方法

预测矫正方法

  • 考虑四阶方法
    • 利用四阶单步法计算起始值 \(w_0,w_1,w_2,w_3\)
    • 利用四步显式 Adams-Bashforth 方法计算 \(w_4\)
    • 利用三步隐式 Adams-Moulton 方法进行矫正

可变步长多步方法

  • 预测、矫正、根据矫正的误差选择新的步长

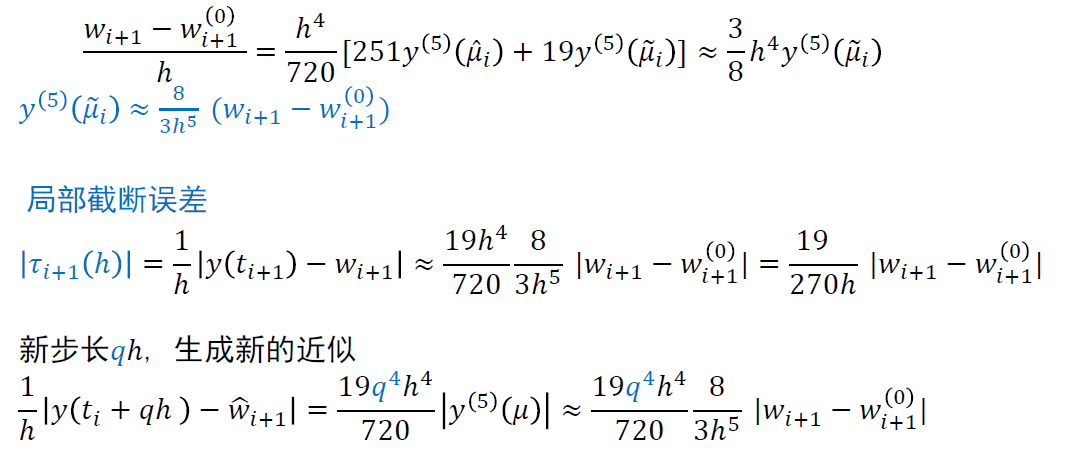
外推方法

  • 外推方法引入更多函数计算改进近似精度
    • 消去低阶项
  • 例子如下

稳定性

  • 相容一致（consistent）
    • 局部截断误差至少一阶

\[ \lim_{h\to0}\max_{1\le i\le N}\vert{\tau_i(h)}\vert=0 \]

  • 收敛

\[ \lim_{h\to0}\max_{1\le i\le N}\vert{w_i-y(t_i)}\vert=0 \]

单步方法

  • 相容一致只需要证明红框内部分即可

多步方法

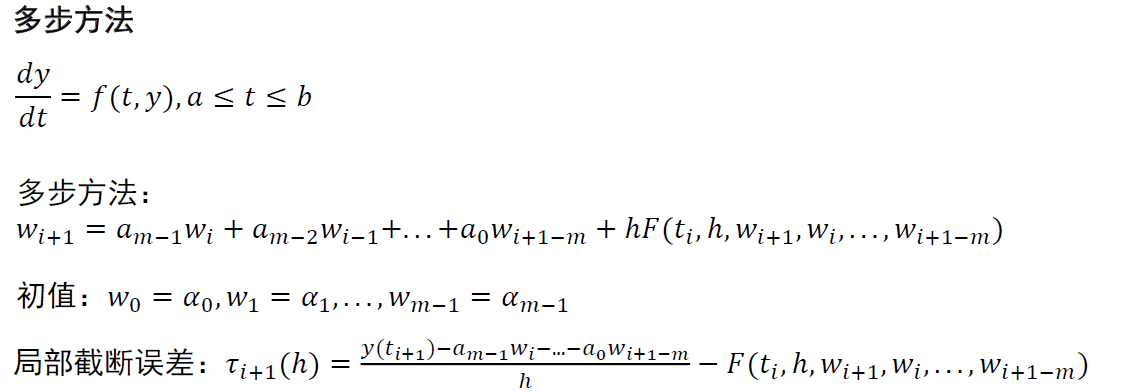
  • 在如下两个假设之下定义收敛、一致

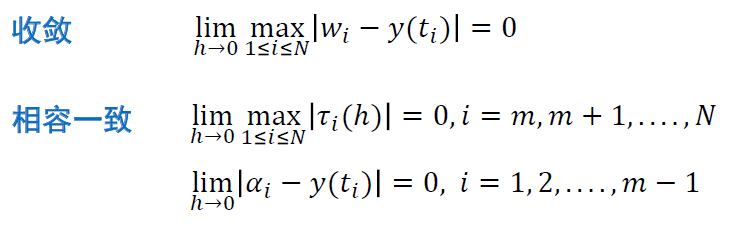
  • 多步方法特征多项式

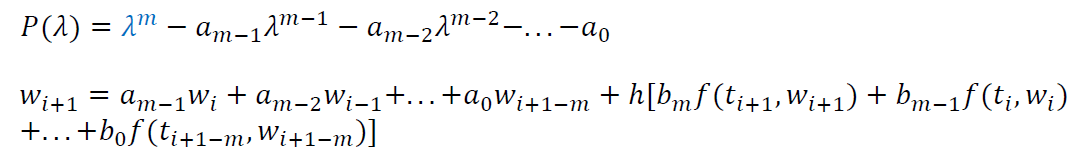
  • 根条件
    • \(\lambda_i\le1\)，所有绝对值为 1 的根都是单根
  • 多步方法稳定当且仅当其满足根条件
  • 如果方法与微分方程相容一致，则该方法稳定当且仅当其收敛
  • 稳定性
    • 强稳定（满足根条件，绝对值为 1 的根只有 1）
    • 弱稳定（满足根条件，，绝对值为 1 的根不止一个）
    • 不稳定（不满足根条件）