计算方法B.裴玉茹.09.常微分方程(4)

Posted on Edited on In Views:
多步方法、如何构造多步方法、显式多步方法（Adam-Bathforth）、隐式多步方法（Adam-Moulton）、隐式方法与数值积分
  • 数值分析课本第 6 章（常微分方程） + PPT（常微分方程）

常微分方程

7. 多步方法

  • 单步方法：使用 \(w_i\) 的知识计算得到 \(w_{i+1}\)
  • 多步方法：使用 \(w_i\) 以及其他的值（\(w_{i-1},\cdots\)）计算得到 \(w_{i+1}\)
    • 能够达到和单步方法相同的精度
    • 将复杂的计算转化为之前己经计算过的值的插值

7.1 构造多步方法

Adam-Bashforth 两步方法

\[ w_{i+1}=w_i+h\left(\dfrac{3}{2}f(t_i,w_i)-\dfrac{1}{2}f(t_{i-1},w_{i-1})\right) \]

  • 之前的二阶求解方法需要计算两次函数值，Adam-Bathforth 方法只需要计算一次
  • 初始的时候，需要先使用单步方法计算得到 \(w_1\)，才能够开始使用该算法
  • 一般的 \(s\) 步方法的形式

\[ w_{i}=a_1w_i+\cdots+a_sw_{i-s+1}+h[b_0f(t_{i+1},w_{i+1})+\cdots b_sf(t_{i-s+1},w_{i-s+1})] \]

  • \(b_0=0\)：显式方法
  • 如何构造多步方法？
    • 泰勒展开

二步方法的构造

\[ w_{i+1}=a_1w_i+a_2w_{i-1}+h[b_0f(t_{i+1},w_{i+1})+b_1f(t_{i},w_{i})+b_2f(t_{i-1},w_{i-1})] \]

  • 假设前面的 \(w_i\) 都正确，\(y'=f_i=f(t_i,w_i)\)，泰勒展开如下

7.2 显式多步方法

  • \(b_0=0\)
  • 二阶方法

\[ \begin{aligned} a_1+a_2&=1\\ -a_2+b_1+b_2&=1\\ a_2-2b_2&=1\\ \end{aligned} \]

  • 因此有无穷个二阶方法

\[ \begin{aligned} a_2&=1-a_1\\ b_1&=2-\dfrac{1}{2}a_1\\ b_2&=-\dfrac{a_1}{2}\\ \end{aligned} \]

  • 局部截断误差：

\[ \begin{aligned} e_{i+1}&=y_{i+1}-w_{i+1}\\ &=\left(1+a_2-3b_2\right)\dfrac{h^3}{6}y_i'''+O(h^4)\\ &=\left(4+a_1\right)\dfrac{h^3}{12}y_i'''+O(h^4)\\ \end{aligned} \]

构造二阶显式方法

\(a_1=1\)
  • 二阶的 Adam-Bathforth 方法
  • 局部截断误差

\[ \dfrac{5h^3}{12}y_i'''+O(h^4)\\ \]

\(a_1=\dfrac{1}{2}\)
  • 算法

\[ w_{i+1}=\dfrac{1}{2}w_i+\dfrac{1}{2}w_{i-1}+h\left(\dfrac{7}{4}f_i-\dfrac{1}{4}f_{i-1}\right) \]

  • 局部截断误差

\[ \dfrac{3h^3}{8}y_i'''+O(h^4) \]

\(a_1=-1\)
  • 算法

\[ w_{i+1}=-w_i+2w_{i-1}+h\left(\dfrac{5}{2}f_i+\dfrac{1}{2}f_{i-1}\right) \]

  • 局部截断误差

\[ \dfrac{h^3}{4}y_i'''+O(h^4) \]

稳定性问题
  • \(a_1=1\)，\(a_1=-1\)

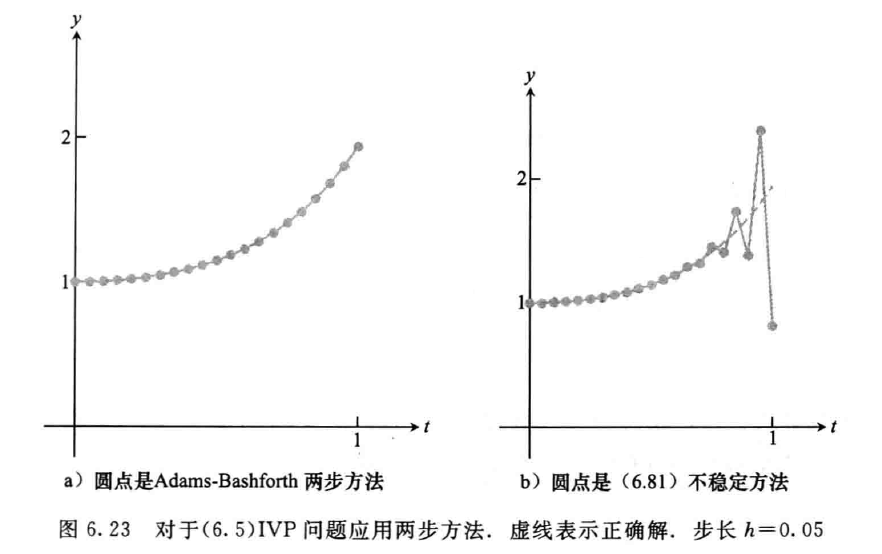
  • 一个例子

\[ \begin{aligned} y'&=0\\ y(0)&=0\\ t&\in[0,1]\\ \end{aligned} \]

  • 使用 \(a_1=-1\) 进行迭代

\[ w_{i+1}=-w_i+2w_{i-1} \]

  • 显然 \(y=0\) 是一个根，但是还有其他根
    • \(w_i=c\lambda^i\) 代入

\[ c\lambda^{i-1}(\lambda-1)(\lambda+2)=0 \]

  • 此时 \(\lambda_2=-2\) 这个根导致了不稳定，小的舍入误差/截断误差，会被无限放大，计算出错
  • 因此稳定的要求就是特征多项式的根的绝对值的界为 \(1\)

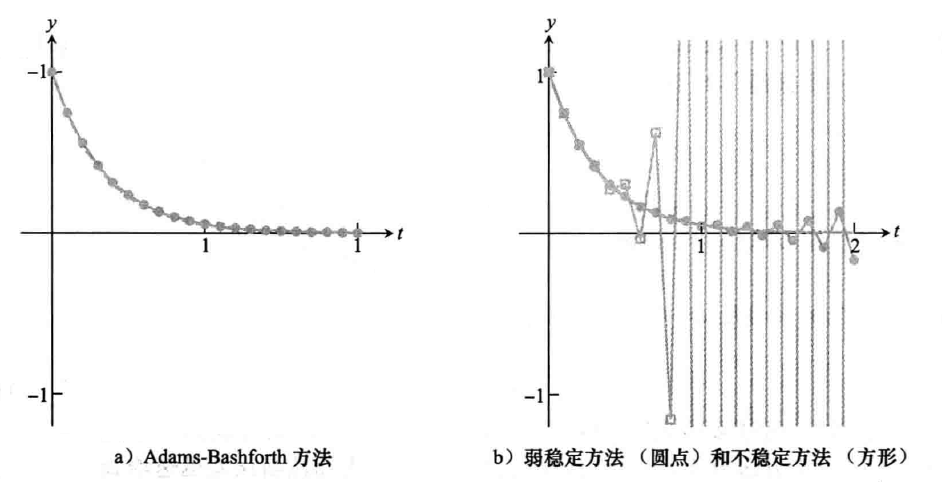
稳定性

  • \(a_1=0\)，此时

\[ w_{i+1}=w_{i-1}+2hf_i \]

  • 弱稳定，\(\lambda=\pm1\)
  • 对比图

收敛性

  • 特征多项式的一个根必须为 1（\(\sum{a_i}=1\)）
    • Adams- Bashforth方法属于其他根都是 0 的情况，因此，Adams-Bashforth 更高阶方法被认为是最稳定的两步方法

高阶 Adam-Bathforth

  • 推导方法和之前完全一致

7.3 隐式多步方法

  • \(b_0\ne0\)

隐式梯形方法

  • 二阶
    • 证明的话和上面类似
    • 验证的话带入验证即可

\[ w_{i+1}=w_i+\dfrac{h}{2}(f_{i+1}+f_i) \]

  • 也被称为是 Adam-Moulton 单步方法

Adam-Moulton 两步方法

  • 三阶

\[ w_{i+1}=w_i+\dfrac{h}{12}(5f_{i+1}+8f_i-f_{i-1}) \]

  • 由于引入了新的变量，可以多带一个方程，精度升了一阶

\[ \begin{aligned} a_1+a_2&=1\\ -a_2+b_0+b_1+b_2&=1\\ a_2+2b_0-2b_2&=1\\ -a_2+3b_0+3b_2&=1\\ \end{aligned} \]

  • 化简

\[ \begin{aligned} a_2&=1-a_1\\ b_0&=\dfrac{1}{3}+\dfrac{1}{12}a_1\\ b_1&=\dfrac{4}{3}-\dfrac{2}{3}a_1\\ b_2&=\dfrac{1}{3}+\dfrac{5}{12}a_1\\ \end{aligned} \]

  • 令 \(a_1=1\) 即可
  • 局部截断误差

\[ y_{i+1}-w_{i+1}=-\dfrac{a_1}{24}h^4y_i^{(4)}+O(h^5) \]

  • 强稳定

隐式方法评价

  • 好处
    • 仅仅使用前面的两步，就可以得到稳定的三阶隐式方法
      • 多引入了一个变量，可以允许多一个方程（高一阶）
    • 隐式方法对应的局部截断误差更小
  • 问题
    • 需要额外处理计算隐式部分
  • 因此，隐式方法通常用于 “预测-矫正” 对中的矫正
    • 同时使用相同阶的隐式和显式方法
    • 每步是显式方法的预测和隐式方法的矫正的组合，其中隐式方法使用预测的 \(w_{i+1}\) 来计算 \(f_{i+1}\)
    • 预测-矫正方法大约使用两倍的计算代价
      • 这是由于在预测和矫正过程中都需要对微分方程右侧的函数 \(f\) 进行求值
    • 通常获取的精度和稳定性使得这个代价完全值得
  • 例子（二阶）
    • Adam-Bathforth 两步显式方法做作为预测
    • Adam-Moulton 单步方法作为矫正

Milne-Simpson 方法

  • \(a_1=0\)，此时为 \(4\) 阶方法

\[ w_{i+1}=w_i+\dfrac{h}{3}(f_{i+1}+4f_i+f_{i-1}) \]

  • 弱稳定

ODE 与数值积分

\[ y(t_{i+1})-y(t_i)=\int_{t_i}^{t_{i+1}}f(t,y)\;\mathrm{d}t \]

  • 梯形法则

\[ y(t_{i+1})-y(t_i)=\dfrac{2}{h}(f_{i+1}+f_i)+O(h^2) \]

  • Simpson 法则

\[ w_{i+1}=w_i+\dfrac{h}{3}(f_{i+1}+4f_i+f_{i-1})+O(h^4) \]

高阶 Adam-Moulton 方法