计算方法B.裴玉茹.09.常微分方程(3)

Posted on In Views:
可变步长方法、嵌入对（RK 2/3、RKF 4/5）、刚性方程（stiff）、隐式方法
  • 数值分析课本第 6 章（常微分方程） + PPT（常微分方程）

常微分方程

5. 可变步长方法

  • 最常见的是使用两个不同阶的方法，称为嵌入对（embedded pair）

5.1 龙格-库塔嵌入对

  • 可变步长方法的关键思想是检测当前步生成的误差
  • 思路：用户设置的容差需要在当前步满足
    • 如果超出容差，则拒绝误差，并且将步长减小
    • 如果满足容差，则接受，并选择下一步适合的步长
      • 例如如果误差小于容差的 \(\dfrac{1}{10}\)，则在接受本步之后加大步长
  • 容差设置
    • 绝对误差：\(e_i\)
    • 相对误差：\(\dfrac{e_i}{w_i}\)
    • 混合方式：\(\dfrac{e_i}{\max\{w_i,\theta\}}\)
      • 避免过小的 \(w_i\)
  • 改变步长最简单的方式：\(\dfrac{h}{2},2h\)
  • 选择合适步长的方式和求解器相关
  • \(p\) 阶求解器，局部截断误差 \(O(h^{p+1})\)
  • 设 \(T\) 为每步中用户允许的相对容差
    • 要求 \(\dfrac{e_i}{w_i}<T\)

减小步长

  • 满足的条件下，如何选择下一步步长？
    • 这里使用相对误差，可以修改为混合误差表示
  • 假设存在常数 \(c\) 满足下式

\[ e_i\approx ch^{p+1} \]

  • 满足条件的最优步长

\[ T\vert{w_i}\vert=ch^{p+1} \]

  • 解得
    • \(0.8\) 表示我们使用更保守的方法

\[ h_{\ast}={\color{red}0.8}\left(\dfrac{T\vert{w_i}\vert}{e_i}\right)^{1/(p+1)}h_i \]

增大步长

  • 不满足容差要求则反复测试，增大步长（例如 \(2h\) ），直至满足容差要求

龙格-库塔嵌入对

  • 在运行当前求解器的同时，运行更高阶的求解器
    • 当前估计：\(w_{i+1}\)
    • 更高阶的估计：\(z_{i+1}\)
    • \(e_{i+1}=\vert{z_{i+1}-w_{i+1}}\vert\) 用于估计从 \(t_i\) 步到 \(t_{i+1}\) 步的误差
  • 如何降低计算代价：共享必要的计算

RK 2/3

  • 尽管步长策略对于 \(w_{i+1}\) 可行，但是使用更高阶的 \(z_{i+1}\) 继续做这步会更有意义，因为已经得到了这个高阶估计，这被称为局部外推

Bogacki-Shampine 2/3 嵌入对

5.2 4/5 阶方法

RKF 4/5

Dormand-Prince 4/5

刚性方程

  • stiff
  • 虽然似乎可变步长的龙格-库塔方法是 ode 求解器中最好的一个，但是仍然有几类方程它们也不能很好处理

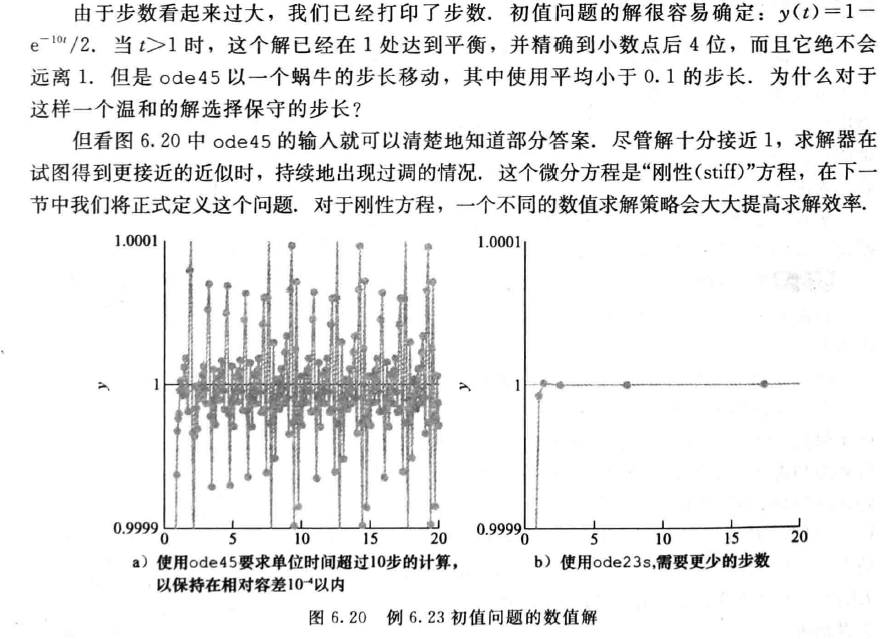
  • 使用 ode23 步数更少

6. 隐式方法与刚性方程

  • 显式方法：新的近似 \(w_{i+1}\) 有一个由已知数据表示的显式公式
  • 某些问题是用显示方法求解效果很差
    • 例如上面的问题，复杂的可变步长的求解器一直在正确解周围过调
    • 原因：在正确解附近 \(h\) 区间的起点和终点斜率变化剧烈

6.1隐式方法与刚性方程

刚性现象

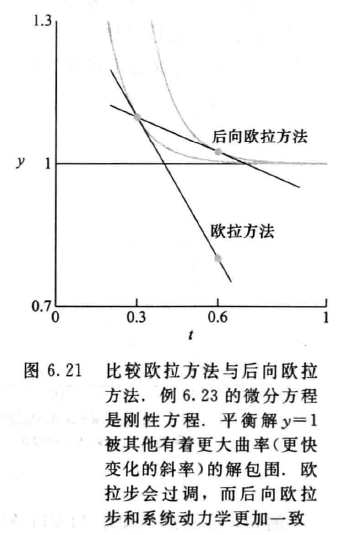
  • 还是上面的例子：\(f(t,y)=10(1-y)\)

  • 欧拉方法

\[ w_{i+1}=w_i+h10(1-w_i)=w_i(1-10h)+10h \]

  • 看成是不动点迭代方法，如果斜率小于 \(1\)，就能收敛
    • \(0<h<0.2\)
  • 因此调整步长大于 \(0.2\) 的时候，很快的从正确解附近离开了 ，这是因为在正确解的附近，斜率变化太快导致的
  • 刚性方程
    • 具有这种性质的微分方程，即吸引解被附近的更快变化的解所包围，被称为刚性方程
    • 这通常是系统具有多时间尺度的标志
    • 定量地讲，这对应微分方程右侧函数 \(f\) 对于 \(y\) 的线性部分，这部分很大并且是负的
      • 对于方程组，这对应很大并且负的线性部分的特征值
    • 这个定义是相对的，但这是刚性的本质，即越负，步长就必须越小以避免过调

后向欧拉方法

\[ \begin{aligned} w_0&=y_0\\ w_{i+1}&=w_i+hf(t_{i+1},w_{i+1})\\ \end{aligned} \]

  • 不同于欧拉方法使用步长区间左侧的斜率，后向欧拉则穿过区间使用右侧的斜率
  • 是隐式方法
  • 对于上面的例子，我们能够很快的得到表达式
    • 因为是线性的

\[ w_{i+1}=w_i+10h(1-w_{i+1})\Longrightarrow w_{i+1}=\dfrac{w_i+10h}{1+10h} \]

  • 但是对于一般的例子，我们很难很快求得隐式方法的解析式，需要采用间接的方式
后向欧拉方法求解的例子
  • IVP 如下

\[ \begin{aligned} y'&=y+8y-9y^3\\ y(0)&=\dfrac{1}{2}\\ t&\in[0,3]\\ \end{aligned} \]

  • 平衡解：\(y=1\)（令 \(y'=0\)）
    • 偏导数为 \(-10\)
    • 刚性问题
      • 欧拉方法 + 带有上界的 \(h\)
      • 后向欧拉方法
  • 后向欧拉方法迭代公式

\[ w_{i+1}=w_i+h(w_{i+1}+8w_{i+1}^2-9w_{i+1}^3) \]

  • 重写

\[ z=w_i+h(z+8z^2-9z^3) \]

  • 牛顿法迭代求解（看成不动点迭代问题）
    • 初始估计
      • 前面近似的 \(w_i\)
      • 欧拉方法得到的 \(w_{i+1}\)
        • 对于刚性问题而言并不是一个好的初始估计
  • 牛顿迭代公式

\[ z_{new}=z-\dfrac{9hz^3-8hz^2+(1-h)z-w_i}{27hz^2-16hz+1-h} \]

  • 对于每一个欧拉后向步，都需要使用牛顿法迭代求解
评价
  • 被称为刚性求解器的方法，诸如后向欧拉方法，允许在相对较大的步长中具有足够的误差控制，以及更好的效率