计算方法B.裴玉茹.09.常微分方程(2)

• 数值分析课本第 6 章（常微分方程） + PPT（常微分方程）

常微分方程

3. 常微分方程组

• 两个物理系统：钟摆、轨道力学
  • 对于这两个系统的仿真促使了大量 ODE 求解器的开发
• 微分方程的阶：出现在方程中最高阶的导数
• 初值问题中，每一个变量都需要有他自己的初值
• 一个二元微分方程组的欧拉方法求解
  • 确定两个变量的步长（可以都为 \(h\)）
  • 根据 \(w_{i,1},w_{i,2}\) 通过和之前一样的欧拉方法求解 \(w_{i+1,1},w_{i+1,2}\)

3.1 高阶方程

• 单个的高阶微分方程可以转化为一个方程组
• 原始高阶方程

\[ y^{(n)}=f(t,y,y',\cdots,y^{(n-1)}) \]

• 重新定义变量

\[ \begin{aligned} y_1&=y\\ y_2&=y'\\ &\cdots\\ y_n&=y^{(n-1)}\\ \end{aligned} \]

• 此时原始的常微分方程转化为 \(1\) 阶

\[ y^{(n)}=f(t,y_1,y_2,\cdots,y_n) \]

• 此时可以使用之前的方法求解
  • 欧拉方法、显式梯形方法等
• 由于可以将高阶方程转化为一阶方程组，我们将仅仅关注一阶方程组
• 同时高阶方程组也可以相同的方式转化为一阶方程组

3.2 计算机仿真：钟摆

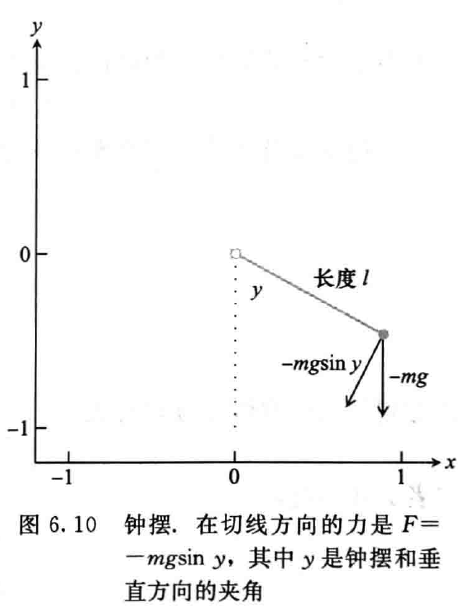
无衰减钟摆

• 无摩擦的运动方程

\[ mly''=F=-mg\sin{y} \]

• 化简得到

\[ y''=-\dfrac{g}{l}\sin{y} \]

• 初始条件：初始角度 \(y(0)\)，初始角速度 \(y'(0)\)
• 转化为一阶方程组：\(y_1=y,y_2=y'\)

\[ \begin{aligned} y_1'&=y_2\\ y_2'&=-\dfrac{g}{l}\sin{y_1}\\ \end{aligned} \]

• 书中有 matlab 仿真的动画代码
  • \(g=9.81\)
• 欧拉方法效果不佳，显式梯形方法就相对不错

衰减钟摆

\[ \begin{aligned} y_1'&=y_2\\ y_2'&=-\dfrac{g}{l}\sin{y_1}-dy_2\\ \end{aligned} \]

• 衰减系数 \(d>0\)，最终稳定于 \(y_1=y_2=0\)

受力衰减钟摆

\[ \begin{aligned} y_1'&=y_2\\ y_2'&=-\dfrac{g}{l}\sin{y_1}-dy_2+A\sin{t}\\ \end{aligned} \]

• 当添加力后，大量的动态行为都变成可能
• 对于微分方程的二维自治系统（右边与 \(t\) 无关），Poincare-Bendixson 定理（来自微分方程理论）指出轨迹都将趋向于规律运动
  • 钟摆最下位置的稳定平衡
  • 像钟摆永远来回摆动的稳定周期循环
    • \(d=1,A=10\)
• 附加的力使得系统非自治（可重写为三维的自治系统，但不是二维的自治系统），因而允许第三种类型的轨迹，即混乱轨迹
  • \(d=1,A=15\)

双钟摆

• 双钟摆由两个简单钟摆组成，其中一个钟摆挂在另外一个钟摆上
• 如果 \(y_1\) 和 \(y_3\) 是两个钟摆相对于垂直方向的角度，微分方程系统如下

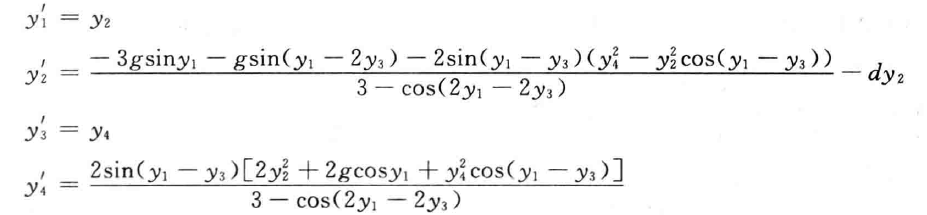
• \(l_1=l_2=1\)
• \(d\)​ 表示旋转轴的摩擦
• \(d=0\) 时，对于许多初始条件，双钟摆都表现为持续的非周期运动

3.3 计算机仿真：轨道力学

• 万有引力

\[ F=\dfrac{gm_1m_2}{r^2} \]

单体问题

• 在单体问题中，一个物体相对于另外一个物体的作用力被认为可忽略（一种简化）
  • 小卫星绕着大行星转动的情况下，我们可以忽略卫星对于行星的力，因而行星可认为是固定的

模拟

• 大物体：\((0,0)\)，小物体：\((x,y)\)
• 力的方向向量

\[ \left(-\dfrac{x}{\sqrt{x^2+y^2}},-\dfrac{y}{\sqrt{x^2+y^2}}\right) \]

• 得到二阶方程组如下

\[ \begin{aligned} m_1x''&=-\dfrac{x}{\sqrt{x^2+y^2}}\times\dfrac{gm_1m_2}{x^2+y^2}=-\dfrac{gm_1m_2x}{(x^2+y^2)^{3/2}}\\ m_1y''&=-\dfrac{y}{\sqrt{x^2+y^2}}\times\dfrac{gm_1m_2}{x^2+y^2}=-\dfrac{gm_1m_2y}{(x^2+y^2)^{3/2}}\\ \end{aligned} \]

• 转化为一阶方程组

\[ \begin{aligned} x'&=v_x\\ v_x'&=-\dfrac{gm_2x}{(x^2+y^2)^{3/2}}\\ y'&=v_y\\ v_y'&=-\dfrac{gm_2y}{(x^2+y^2)^{3/2}}\\ \end{aligned} \]

• 单体问题的解一定是圆锥曲线（椭圆、抛物线、双曲线）
• 单体问题是虚构的，由于它忽略了卫星对于（非常大的）的行星的力，包含后者得到的两个物体的运动被称为二体问题

三体问题

• 三个物体在重力的作用下交互运动，被称为三体问题
• 即使所有的运动都被局限在平面（受限三体问题），从本质上也可能难以预测长期的轨迹
• 非预测性来自于对初值条件的敏感依赖
• 受限三体问题没一个物体都有 4 个方程
  • 例如物体 1 的方程如下

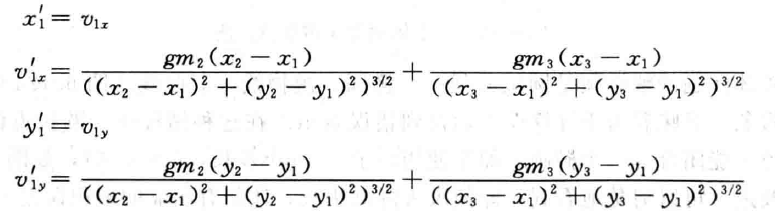
4. 龙格-库塔方法和应用

• 龙格-库塔方法是一组 ODE 求解器，包含欧拉和梯形方法，以及更加复杂的高阶方法

4.1 龙格-库塔家族

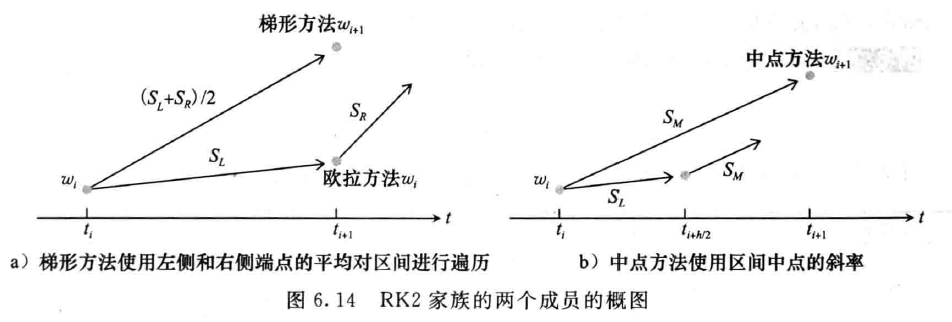
中点方法

\[ \begin{aligned} w_0&=y_0\\ w_{i+1}&=w_i+hf\left(t_i+\dfrac{h}{2},w_i+\dfrac{h}{2}f(t_i,w_i)\right) \end{aligned} \]

局部截断误差

• 泰勒展开

\[ y_{i+1} =y(t_i)+hf(t_i,y_i)+\dfrac{h^2}{2}\left(\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)f(t_i,y_i)\right)+\dfrac{h^3}{6}y'''(c) \]

• 中点方法，二维泰勒展开

\[ \begin{aligned} w_{i+1}&=w_i+hf\left(t_i+\dfrac{h}{2},y_i+\dfrac{h}{2}f(t_i,y_i)\right)\\ &=w_i+h\left(f(t_i,y_i)+\dfrac{h}{2}\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+\dfrac{h}{2}f(t_i,y_i)\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)+O(h^2)\right)\\ \end{aligned} \]

• 对比，得到局部截断误差

\[ e_{i+1}=y_{i+1}-w_{i+1}=O(h^3) \]

• 中点方法是 \(2\) 阶方法

RK2

• 右侧的每个函数的求值被称为方法的阶段（stage）
• 梯形方法和中点方法都是二阶段的二阶龙格-库塔方法家族中的成员（RK2）
• RK2 的一般形式如下（\(\alpha\ne0\)）

\[ w_{i+1}=w_i+h(1-\dfrac{1}{2\alpha})f(t_i,w_i)+h\dfrac{1}{2\alpha}f(t_i+\alpha h,w_i+\alpha hf(t_i,w_i)) \]

• 显式梯形方法：\(\alpha=1\)
• 中点方法：\(\alpha=\dfrac{1}{2}\)

局部截断误差

• 泰勒展开

\[ y_{i+1} =y(t_i)+hf(t_i,y_i)+\dfrac{h^2}{2}\left(\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)f(t_i,y_i)\right)+\dfrac{h^3}{6}y'''(c) \]

• 中点方法，二维泰勒展开

\[ \begin{aligned} w_{i+1}&=w_i+h(1-\dfrac{1}{2\alpha})f(t_i,w_i)+h\dfrac{1}{2\alpha}f(t_i+\alpha h,w_i+\alpha hf(t_i,w_i))\\ &=w_i+h\left(f(t_i,y_i)+\dfrac{1}{2\alpha}\left( \alpha h\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+\alpha hf(t_i,y_i)\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)+O(h^2) \right)\right)\\ &=w_i+h\left(f(t_i,y_i)+\dfrac{h}{2}\left( \dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+f(t_i,y_i)\dfrac{\partial{f}}{\partial{y}}(t_i,y_i) \right)\right)+O(h^3)\\ \end{aligned} \]

• 局部截断误差

\[ e_{i+1}=y_{i+1}-w_{i+1}=O(h^3) \]

RK4

• 一种常见的龙格-库塔方法

\[ \begin{aligned} w_{i+1}&=w_i+\dfrac{h}{6}(s_1+2s_2+2s_3+s_4)\\ s_1&=f(t_i,w_i)\\ s_2&=f(t_i+\dfrac{h}{2},w_i+\dfrac{h}{2}s_1)\\ s_3&=f(t_i+\dfrac{h}{2},w_i+\dfrac{h}{2}s_2)\\ s_4&=f(t_i+h,w_i+hs_3)\\ \end{aligned} \]

• 证明类似
  • 泰勒展开，但是很复杂
  • 方法是 4 阶的，所以局部截断误差是 5 阶的，展开得展开麻了
• 简单、容易编程实现
• 这是单步方法，仅需要一个初始条件
• 作为 4 阶方法，比欧拉方法或者梯形方法要精确得多

4.2 计算机仿真：Hodgkin-Huxley 神经元

4.3 计算机仿真：Lorenz 方程

• 气象学

• 对于初值极度敏感：混沌现象