计算方法B.裴玉茹.09.常微分方程

• 数值分析课本第 6 章（常微分方程） + PPT（常微分方程）

常微分方程

• 微分方程是包含导数的方程

\[ y'(t)=f(t,y(t)) \]

1. 初值问题

1.0 logistic 方程

• 逻辑斯蒂方程（logistic）

\[ y'=cy(1-y) \]

• 常微分方程一般具有无穷多的解
• 通过定义初始条件，我们可以找出无穷多解中我们感兴趣的那个
• 一阶常微分方程的初值问题由两部分组成
  • 方程
  • 在指定区间 \([a,b]\) 上的初值条件

\[ \begin{array}{c} y'=f(t,y)\\ y(a)=y_a\\ t\in[a,b] \end{array} \]

• 自主的方程
  • \(f(t,y)\) 与 \(t\) 无关
• 将微分方程当作斜率场（方向场）

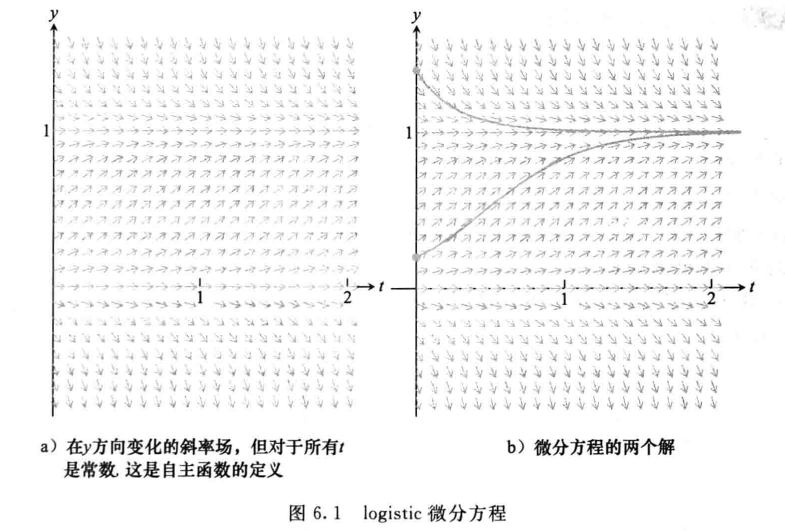
• 当 \(y_0\ne1\) 时，上述初值问题的解为

\[ y=1-\dfrac{1}{1+\dfrac{y_0}{1-y_0}e^{ct}} \]

• \(y_0=1\Longrightarrow y=1\)

1.1 欧拉方法

• 在一般的情况中，微分方程没有显式的解公式

几何求解方式

• 流程
  • 画出斜率图
  • 通过跟随箭头计算 “求解” 微分方程
• 有误差
  • 如果正确的解斜率变化缓慢，则这样的解法是一个比较好的近似
• 这便是欧拉方法

欧拉方法

\[ \begin{aligned} w_0&=y_0\\ w_{i+1}&=w_i+hf(t_i,w_i) \end{aligned} \]

• 其中 \(h\) 表示步长
• 随着步长的减小，截断误差在变小

欧拉方法收敛性

\[ \begin{array}{c} y'=cy\\ y(0)=y_0\\ t\in[0,1] \end{array} \]

• 欧拉方法，对于固定的 \(t\in(0,1]\) 设步长 \(h\) 为 \(\dfrac{t}{n}\)

\[ w_n=(1+hc)^{n}y_0 \]

• \(n\to\infty\)

\[ \begin{aligned} \lim_{n\to\infty}w_n &=\lim_{n\to\infty}(1+\dfrac{tc}{n})^{n}y_0\\ &=\lim_{n'\to\infty}(1+\dfrac{1}{n'})^{ctn'}y_0\\ &=e^{ct}y_0 \end{aligned} \]

• 精确解可以通过分离变量求解，和上面相同
• \(n\to\infty\) 时，上述初值问题使用欧拉方法能够得到精确解

1.2 解的存在性、唯一性、连续性

利普希茨连续

• 利普希茨连续一定连续（定义可证），但是不一定可微
• 更一般的，条件中的矩形可以是凸集

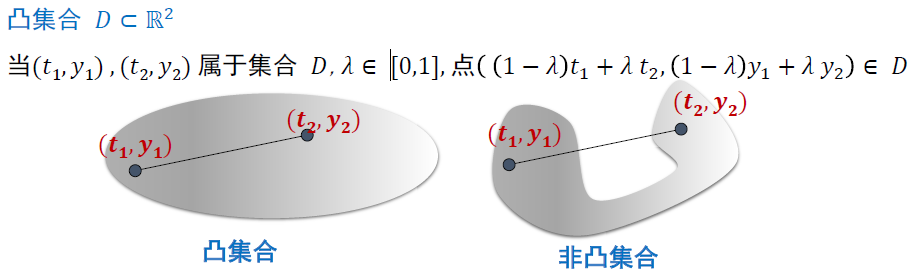
• 如果函数 \(f\) 对 \(y\) 连续可微，则利普希茨常数可以取在这个矩形（凸集）中如下式子的最大值

\[ \left\vert\dfrac{\partial{f}}{\partial{y}}(t,c)\right\vert \]

• 由均值定理保证

\[ \dfrac{f(t,y_1)-f(t,y_2)}{y_1-y_2}=\dfrac{\partial{f}}{\partial{y}}(t,c) \]

存在性和唯一性

• 利普希茨连续假设保证初值问题的解的存在性和唯一性

• 注意不能保证在整个区间上都是有解的
  • 一个简单的原因是解可能超出了 \(y\) 的满足利普希茨常数有效的范围 \([\alpha,\beta]\)
    • 在 \(y\) 方向上超出了凸集的范围
• 定理证明
  • G Birkhoff and G Rota [1989] Ordinary Differential Equations, 4th ed. John Wiley & Sons, New York.

误差放大

• 误差界

证明 (1)

• \(Y(a)=Z(a)\) 时，由唯一解定理，\(Y(t)=Z(t)\) 成立

证明 (2)

• \(Y(a)\ne Z(a)\) 时，此时不妨假设 \(Y(t)\ne Z(t),\forall t\in[a,b]\)，否则在相等的点转化为上面的形式
• 令 \(u(t)=Y(t)-Z(t)\)，此时 \(u(t)\) 恒正或者恒负，定理只使用绝对值，不妨假设 \(u(t)>0\)
• 利普希茨条件

\[ u'(t)=f(t,Y(t))-f(t,Z(t))\le L\vert{Y(t)-Z(t)}\vert=Lu(t) \]

• 于是

\[ (\ln{u})'=\dfrac{u'}{u}\le L \]

• 均值定理

\[ \dfrac{\ln{u(t)}-\ln{u(a)}}{t-a}=(\ln{u(\xi)})'\le L \]

• 转化即得

\[ u(t)\le u(a)e^{L(t-a)} \]

• 证毕

1.3 一阶线性方程

• 右侧是关于 \(y\) 的线性函数
• 考虑初值问题

\[ \begin{array}{c} y'=g(t)y+h(t)\\ y(a)=y_a\\ t\in[a,b] \end{array} \]

• 如果 \(g(t)\) 在区间 \([a,b]\) 上连续，则唯一解存在（都取最大值即可）
  • 利普希茨常数

\[ L=\max_{[a,b]}g(t) \]

显式求解

要求积分因子 \(e^{-\int{g(t)\;\mathrm{d}t}}\) 能够显示表示 \[ \begin{aligned} (y'-g(t)y)e^{-\int{g(t)\;\mathrm{d}t}}&=h(t)e^{-\int{g(t)\;\mathrm{d}t}}\\ (ye^{-\int{g(t)\;\mathrm{d}t}})'&=h(t)e^{-\int{g(t)\;\mathrm{d}t}}\\ ye^{-\int{g(t)\;\mathrm{d}t}}&=\int{h(t)e^{-\int{g(t)\;\mathrm{d}t}}}\\ \end{aligned} \]

• 于是

\[ y=e^{\int{g(t)\;\mathrm{d}t}}\int{h(t)e^{-\int{g(t)\;\mathrm{d}t}}} \]

2. IVP 求解器的分析

• IVP（initial value problem）：初值问题

2.1 局部与全局误差

• 初值问题

\[ \begin{array}{c} y'=f(t,y)\\ y(a)=y_a\\ t\in[a,b] \end{array} \]

• 一步求解器（如欧拉方法）

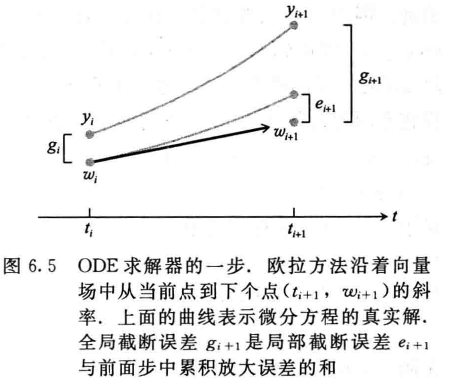
• 单步初值问题

\[ \begin{array}{c} y'=f(t,y)\\ y(t_i)=w_i\\ t\in[t_i,t_{i+1}] \end{array} \]

• 使用 \(z\) 表示单步初值问题的精确解
• 全局截断误差：\(g_i=\vert{w_i-y_i}\vert\)
  • 累计误差
• 局部截断误差：\(e_i=\vert{w_i-z(t_i)}\vert\)
  • 单步误差
• 注意：全局截断误差不是简单的局部截断误差求和

欧拉方法的局部截断误差

• \(t_{i+1}=t_i+h\)
• 泰勒展开

\[ \begin{aligned} y(t_i+h)&=y(t_i)+hy'(t_i)+\dfrac{h^2}{2}y''(c)\\ &=w_i+hf(t_i,w_i)+\dfrac{h^2}{2}y''(c)\\ \end{aligned} \]

• 欧拉方法

\[ w_{i+1}=w_i+hf(t_i,w_i) \]

• 局部截断误差

\[ e_{i+1}=\dfrac{h^2}{2}\vert{y''(c)}\vert \]

• 假设 \(y''\) 在区间 \([a,b]\) 的上界为 \(M\)，于是欧拉方法的局部截断误差的上界如下

\[ e_i\le\dfrac{Mh^2}{2} \]

全局截断误差

• 假设步长不变，都为 \(h\)
• 初始条件，\(y(a)=y_a\)
• 初始全局截断误差：\(g_0=0\)
• 第一步
  • 没有之前的累计误差

\[ g_1=e_1=\vert{w_1-y_1}\vert \]

• 第二步
  • 需要考虑累计误差
  • 第二部分的误差由上面的定理给出

\[ \begin{aligned} g_2&=\vert{w_2-y_2}\vert=\vert{w_2-z(t_2)+z(t_2)-y_2}\vert\\ &\le\vert{w_2-z(t_2)}\vert+\vert{z(t_2)-y_2}\vert\\ &=e_2+e^{Lh}g_1\\ &=e_2+e^{Lh}e_1\\ \end{aligned} \]

• 第 \(i\) 步

\[ \begin{aligned} g_i&\le e_i+e^{Lh}g_{i-1}\\ &\le\cdots\\ &\le e_i+e^{Lh}e_{i-1}+e^{2Lh}e_{i-2}+\cdots+e^{(i-1)Lh}e_1 \end{aligned} \]

• 于是我们得到了一个全局截断误差的上界估计
• 一般的我们如果假设 \(e_i\le Ch^{k+1}\)，于是全局截断误差如下

\[ \begin{aligned} g_i&\le\dfrac{Ch^{k+1}(e^{iLh}-1)}{e^{Lh}-1}\\ &\le\dfrac{Ch^{k+1}(e^{iLh}-1)}{Lh}\\ &=\dfrac{Ch^{k}(e^{iLh}-1)}{L}\\ \end{aligned} \]

• 例如，欧拉方法的全局截断误差
  • \(C=\dfrac{M}{2},k=1\)

\[ g_i\le\dfrac{Ch^{k}(e^{iLh}-1)}{L}=\dfrac{Mh(e^{iLh}-1)}{2L} \]

定理描述

• 如果当 \(h\to0\) 的时候，\(g_i\to0\)，则称上述求解器为 \(k\) 阶方法

欧拉方法的收敛性

• 欧拉方法是 1 阶方法
  • 欧拉方法构造简单，但是阶数低，近似程度不够
  • 优化：提高阶数

2.2 显式梯形方法

\[ \begin{aligned} w_0&=y_0\\ w_{i+1}&=w_i+h\dfrac{f(t_i,w_i)+f(t_i+h,w_i+hf(t_i,w_i))}{2} \end{aligned} \]

• 直观上讲
  • 欧拉方法离散步的斜率从区间 \([t_i,t_{i+1}]\) 的左端点
  • 显式梯形方法离散步的斜率是区间 \([t_i.t_{i+1}]\) 的左右端点均值
• 显式方法：右端点的属性可以通过现有的值计算
• 梯形方法：如果 \(f(t,y)\) 和 \(y\) 无关，那么便是梯形公式
• 也被称为
  • 改进的欧拉方法
  • Heun 方法

局部截断误差

• 对微分方程 \(y'=f(t,y)\) 两边对 \(t\) 求偏导

\[ \begin{aligned} y''(t) &=\dfrac{\partial{f}}{\partial{t}}(t,y)+\dfrac{\partial{f}}{\partial{y}}(t,y)y'(t)\\ &=\dfrac{\partial{f}}{\partial{t}}(t,y)+\dfrac{\partial{f}}{\partial{y}}(t,y)f(t,y)\\ \end{aligned} \]

• 泰勒展开

\[ \begin{aligned} y_{i+1} &=y(t_i+h)\\ &=y(t_i)+hy'(t_i)+\dfrac{h^2}{2}y''(t_i)+\dfrac{h^3}{6}y''(c)\\ &=y(t_i)+hy'(t_i)+\dfrac{h^2}{2}\left(\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)f(t_i,y_i)\right)+\dfrac{h^3}{6}y'''(c)\\ \end{aligned} \]

• 显式梯形方法（二维泰勒展开）

\[ \begin{aligned} &f(t_i+h,y_i+hf(t_i,y_i))\\ =&f(t_i,y_i)+h\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+hf(t_i,y_i)\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)+O(h^2)\\ \end{aligned} \]

• 于是改写

\[ \begin{aligned} w_{i+1} &=y_i+h\dfrac{f(t_i,y_i)+f(t_i+h,y_i+hf(t_i,y_i))}{2}\\ &=y_i+hf(t_i,y_i)+\dfrac{h^2}{2}\left(\dfrac{\partial{f}}{\partial{t}}(t_i,y_i)+f(t_i,y_i)\dfrac{\partial{f}}{\partial{y}}(t_i,y_i)\right)+O(h^3)\\ \end{aligned} \]

• 于是得到局部截断误差

\[ e_{i+1}=y_{i+1}-w_{i+1}=O(h^3) \]

• 显式梯形方法是 \(2\) 阶方法
• 复杂度讨论
  • 显示梯形方法：更高阶，计算函数的次数变成了 2 倍
  • 如何比较：相同计算代价下比较
  • 欧拉方法步长缩短一半，此时计算代价相同，但是此时全局误差只是变成了 \(\dfrac{1}{2}\)，阶数没有改变，因此显式梯形方法更好

2.3 泰勒方法

• 所有阶数的方法都存在
• \(k\) 阶泰勒方法

\[ \begin{aligned} w_0&=y_0\\ w_{i+1}&=w_i+h{f(t_i,w_i)}+\dfrac{h^2}{2}f'(t_i,w_i)+\dfrac{h^3}{6}f''(t_i,w_i)+\cdots+\dfrac{h^k}{k!}f^{(k-1)}(t_i,w_i) \end{aligned} \]

\[ f'(t,y)=f_t(t,y)+f_y(t,y)y'(t)=f_t(t,y)+f_y(t,y)f(t,y) \]

• 很容易得到，局部截断误差为 \(O(h^{k+1})\)，因此是 \(k\) 阶方法

• 一阶泰勒方法就是欧拉方法

二阶泰勒方法

\[ \begin{aligned} w_{i+1}&=w_i+h{f(t_i,w_i)}+\dfrac{h^2}{2}f'(t_i,w_i)\\ &=w_i+h{f(t_i,w_i)}+\dfrac{h^2}{2}(f_{t}(t_i,y_i)+f_y(t_i,y_i)f(t_i,y_i))\\ \end{aligned} \]

• 概念上，泰勒方法告诉我们任何阶的ODE方法都存在
  • 但是，该方法由于计算公式中出现的函数 \(f\) 的偏导数，本身的性能也有损失
  • 由于可以推出相同阶但是不需要计算偏导数的方法，泰勒方法仅仅用于特定的用途