GAMES103.王华民.04.Rigid Contacts

Posted on In Views:
粒子碰撞、penalty 方法、impulse 方法、刚体碰撞、shape matching

刚体碰撞

大纲

  • 粒子的碰撞检测与响应
    • penalty methods
    • impulse methods
  • 基于 impulse methods 的刚体碰撞检测与响应
  • shape matching 方法
    • 物理无关

粒子碰撞

  • Particle Collision Detection and Response

有向距离函数

  • Signed Distance Function
  • 用于表示一个点到某个表面的距离
    • 正负表示内外
      • 内部：负
      • 外部：正
    • 大小表示距离

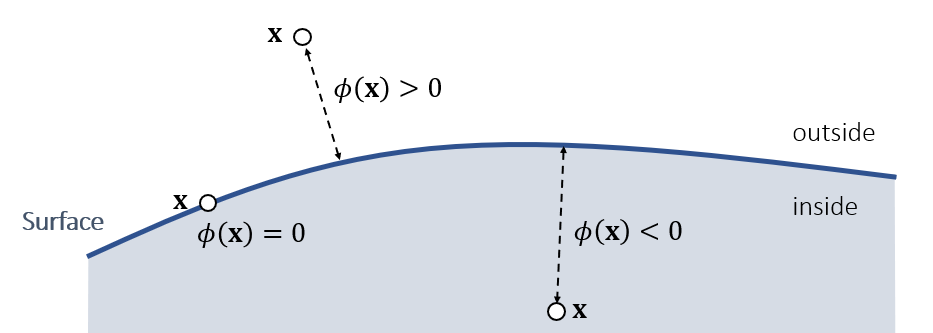
  • 正好在表面上：zero surface

例子

  • 表面、球体、无限长圆柱

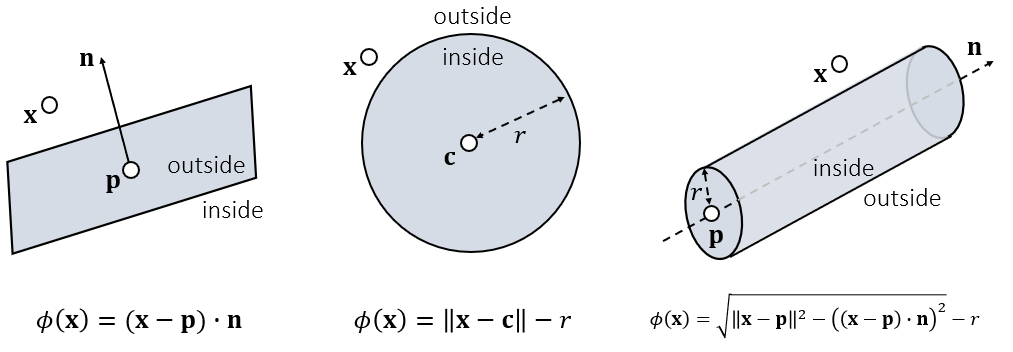
相交计算

  • Intersection

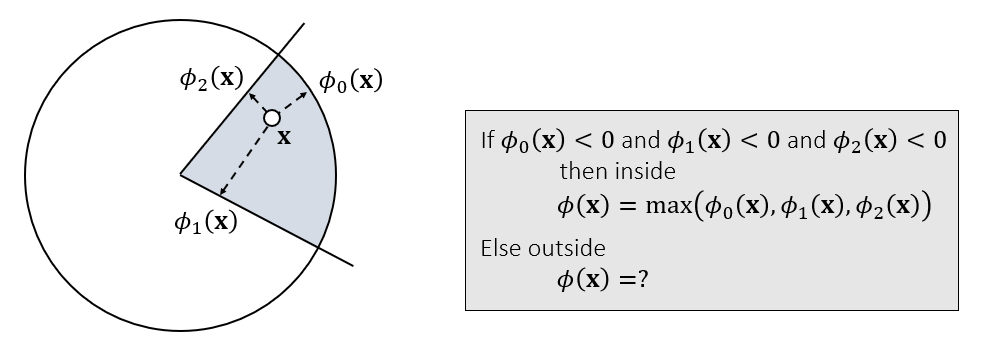
  • 如果都小于 0，则在内部；否则在外部
  • 在内部的时候，取 \(\max\)，因为都是负数
  • 在外部的时候，距离函数不一定是 \(\max\)，可能和这三个值都不相关
    • 对应最小值的那个点，可能不在相交的区域内部
  • 但是碰撞检测我们都不关心外部的情况，因此不需要考虑具体的值（只有内部才相交）

求并计算

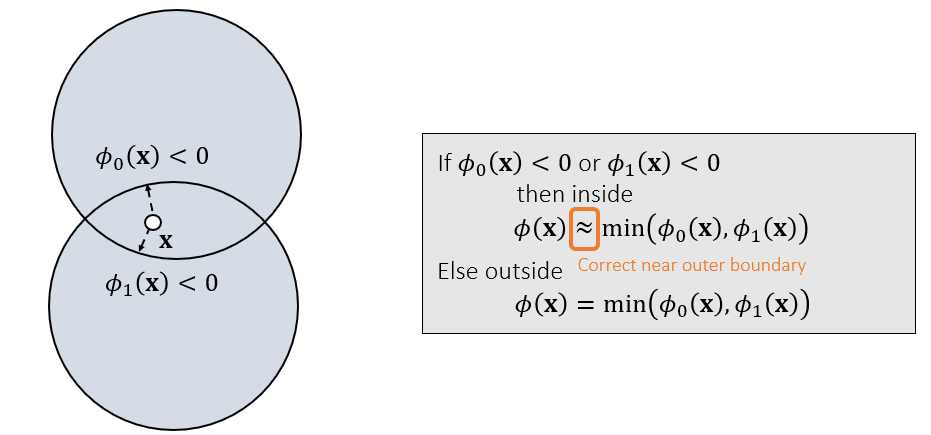
  • 对应求并，在外部则直接取 \(\min\)
  • 在内部则不一定，因为距离最小值对应的点可能不在并集的边界上（例如上图）
    • 假设点比较靠近并集的外表面，可以使用取 \(\min\) 近似
  • 另外一种做法，分别对这两个物体做碰撞检测

碰撞检测

  • 利用有向距离函数做碰撞检测
  • 有 \(\phi(\mathbf{x})<0\)，则发生碰撞

碰撞响应

Penalty Method

  • 设置一个处罚的力，把粒子从内部推出来
  • 效果是滞后的，在下一步迭代中这个力才会生效
Quadratic Penalty Method
  • penalty potential is quadratic
    • 二次
  • 弹簧力的大小正比于 \(\phi(\mathbf{x})\)
  • 弹簧力的方向为对应 \(\phi(\mathbf{x})\) 的点的法向
  • 示意图

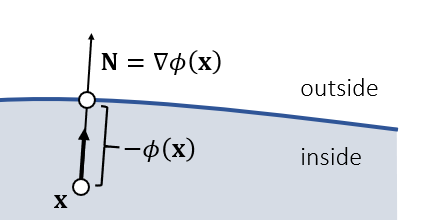
  • 表达式
    • \(k\)：penalty strength

\[ \mathbf{f}=-k\;\phi(\mathbf{x})\;\mathbf{N} \]

  • 问题：只有粒子在内部才产生力
    • 因此只有在穿模发生，才会有里把他推出来
    • artifacts
Quadratic Penalty Method with a Buffer
  • 可以预先加一个范围，当 \(\phi(\mathbf{x})<\epsilon\)，则认为碰撞发生

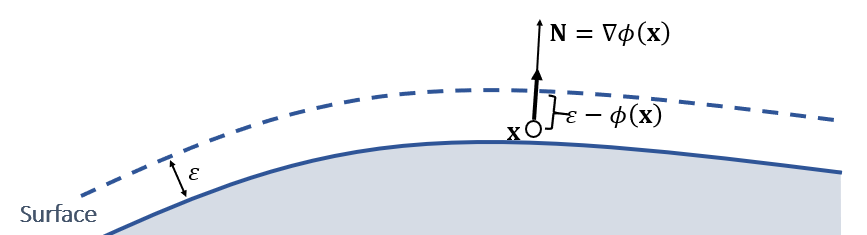
  • 表达式

\[ \mathbf{f}=k\;(\epsilon-\phi(\mathbf{x}))\;\mathbf{N} \]

  • 还是有问题
    • 如何设置 \(k\) ？
      • 太大：一碰就直接飞走了（over shooting）
      • 太小：推不出来
Log-Barrier Penalty Method
  • 动态调整 \(k\) 的大小，和距离相关

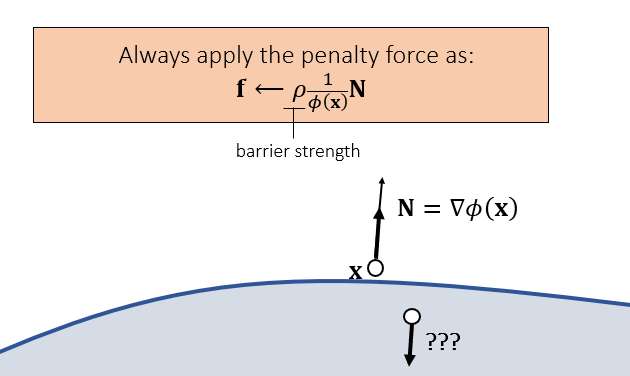
  • 认为在内部不会发生
    • 这样需要调整 \(\Delta{t}\) 的大小才能满足
    • 小步长
  • 为什么叫做 Log-Barrier Penalty Method
    • 力可以认为是能量的导数，能量表达式中有 \(\log\) 的形式
  • 问题
    • over shooting 的发生还是很难避免
      • 离得很近
    • 可能穿透
      • 如果穿透，则会越陷越深
Penalty Method 总结
  • 需要调整步长
    • 减少 overshooting 问题
    • 保证 log-barrier 不穿透
  • 可以给 log-barrier 方法加一个 buffer
    • Li et al. 2020. Incremental Potential Contact: Intersection- and Inversion-free Large Deformation Dynamics. TOG.
    • Wu et al. 2020. A Safe and Fast Repulsion Method for GPU-based Cloth Self Collisions. TOG.
  • 很难做摩擦
    • Frictional contacts are difficult to handle

Impulse Method

  • 希望施加的力在这次迭代中马上有效果，而不滞后
  • 在检测到碰撞之后，马上设置新的状态 \(\mathbf{x},\mathbf{v}\)
位置设定
  • 直接平移到表面

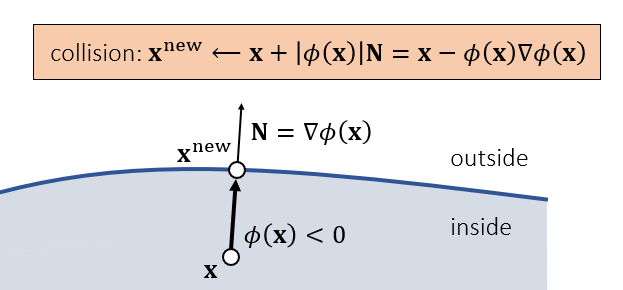
速度设置
  • 考虑摩擦
  • 速度分解：法向 + 切向

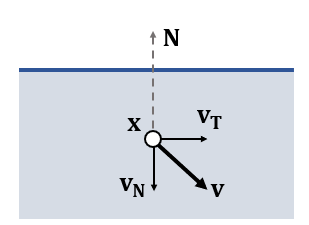
  • 判断速度是否还是继续向物体内部，如果向物体内部则将其修改为朝外
    • 法向分量反向
    • 乘上一个 \([0,1]\) 之间的系数 \(\mu_{\mathbf{N}}\)
  • 考虑摩擦力
    • 切向分量乘上一个摩擦系数 \(a\)
  • 如何设置 \(a\)
    • \(a\) 期望速度下降的最多（越小越好）
    • 需要满足库仑摩擦定律
      • 切向上速度变化不能小于法向上速度变化乘以系数 \(\mu_{\mathbf{T}}\)
        • 摩擦力跟作用在摩擦面上的正压力成正比

  • 流程图

  • 优点是能够加入对摩擦力的控制
  • 处理起来相对比较麻烦
  • 实际应用中
    • 刚体模拟：impulse 方法还是挺多的
    • 布料、弹性体：penalty 方法比较多

刚体碰撞

碰撞检测

  • 如果物体由很多个点组成，可以对这些点遍历，对每一个点进行碰撞检测
    • 如果有一个点碰撞上了，则就是碰撞上了
    • 这种方法比较慢，但是也可以接受

碰撞响应

  • 对于每一个节点，计算出来他们的位置 \(\mathbf{x}_i\) 和速度 \(\mathbf{v}_i\)
    • 不能直接用这些点去更新，因为这些点都是虚拟的，直接更新不能满足刚体的性质
    • 对于刚体而言，只有质心的 4 个属性（\(\mathbf{x,v,q,\omega}\)）

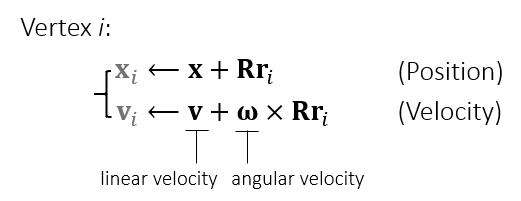
impulse 方法

  • 使用简化的 impulse 方法进行更新
    • 不更新位置，只更新速度
    • 对于刚体而言，直接修改位置状态比较麻烦，修改速度和角速度则相对简单
  • 对整体施加一个冲量 \(\mathbf{j}\)，实现对 \(\mathbf{x,v}\) 的更新

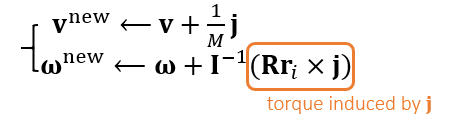
  • 如何设置冲量 \(\mathbf{j}\)
  • 考虑对整体设置了这样的冲量之后对单点的影响，因为我们能够通过上面的方式求得对单点的影响，因此能够反推求出 \(\mathbf{j}\)
  • 如此便能够通过设定 \(\mathbf{j}\) 控制 \(\mathbf{v}_i,\mathbf{\omega}_i\) 的变化

对单点的影响

  • 那么这样施加的冲量对每一个点造成的影响如下

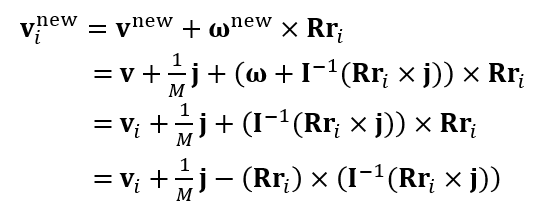
  • 叉乘 \(\mathbf{r}\times\) 等价于一个矩阵乘 \(\mathbf{r}^{\ast}\)

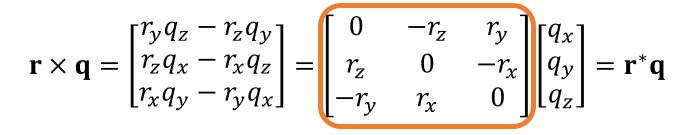
  • 进一步统一如下

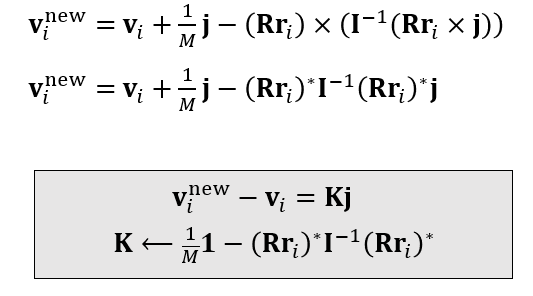
算法

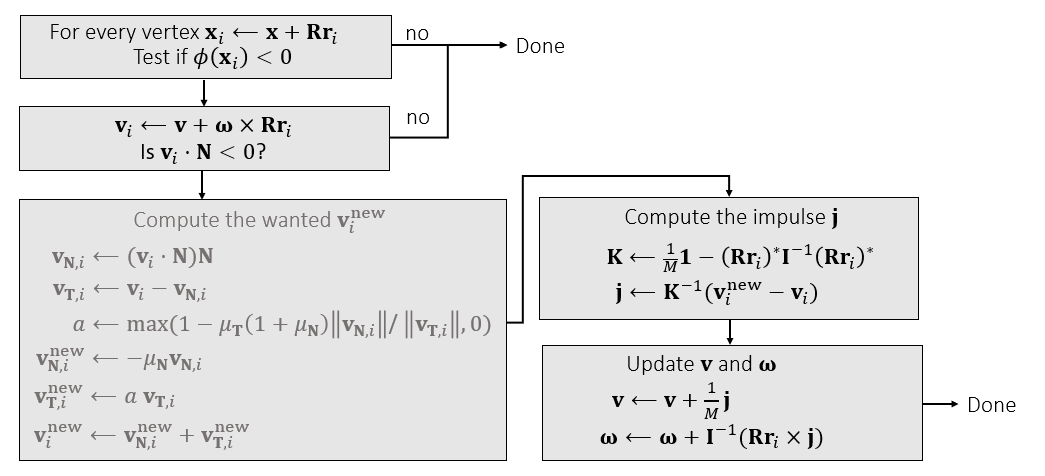
实现细节

  • 有多个点碰撞怎么处理？
    • 求出这些点位置的平均值，对这个点做碰撞响应、计算冲量即可
    • 不建议把每个点都算一遍，这样会导致最终计算得到的冲量偏大
      • 因为其实你这个点计算得到的冲量也会对其他点造成影响
  • 因为重力的存在，会导致物体一直在地面上抖动，掉下来弹上去，掉下来弹上去（oscillation）
    • 加上一个衰减系数 \(\mu_{\mathbf{N}}\)
  • 为什么不直接更新位置？
    • 非线性问题，需要保持刚体的形状，直接更新可能会不满足刚体原来的形状

多个物体的碰撞

  • 求解线性系统，因为他们直接互相影响
  • 参考

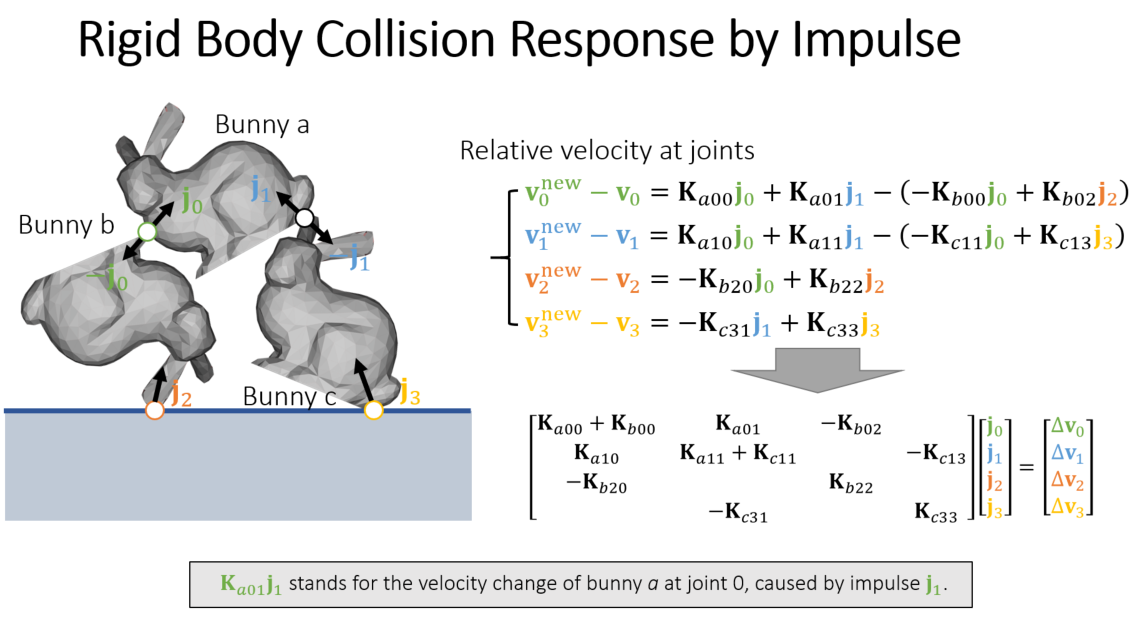
Shape Matching

  • 思想
    • 首先让所有的点沿着速度的方向运动（类似粒子系统）
      • 处理碰撞、摩擦
    • 然后再将形成的新节点聚回去，形成原来的形状

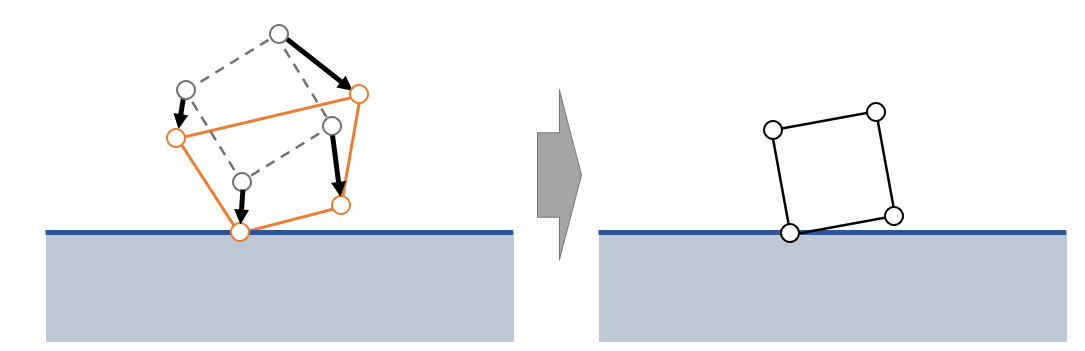
  • 第一步就是做一步简单的粒子模拟
  • 第二步加限制求解比较复杂

限制求解

  • 质心 \(\mathbf{c}\)，旋转矩阵 \(\mathbf{R}\) 不知道，需要求解这两个量
  • 最小二乘

\[ \{\mathbf{c},\mathbf{R}\}=\arg\min\sum_{i}\Vert{\mathbf{c}+\mathbf{R}\mathbf{r}_i-\mathbf{y}_i}\Vert \]

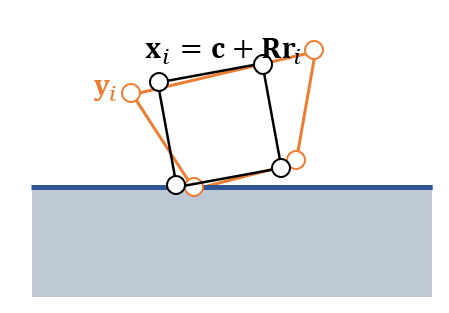
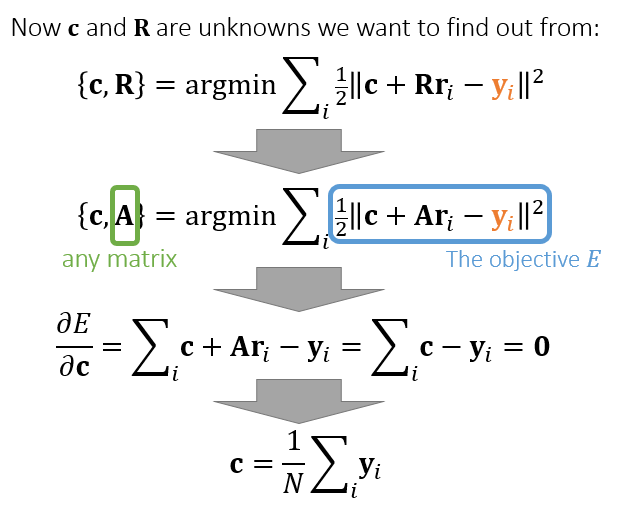
  • 放松限制，任意矩阵 \(\mathbf{A}\) 代替旋转矩阵
  • 求极值，求导
  • 求 \(\mathbf{c}\)
    • \(\sum\mathbf{r}_i=\mathbf{0}\)

  • 求 \(\mathbf{R}\)

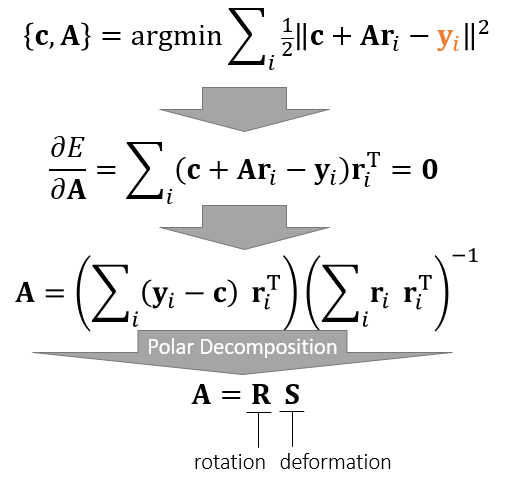
  • 为什么对 \(\mathbf{A}\) 做 polar deformation 能够得到旋转矩阵 \(\mathbf{R}\)
    • 奇异值分解能够得到 3 个变换
    • 经过处理我们能够将其转化为局部旋转 \(\times\) 形变的部分
    • 因为是刚体，我们没有形变，舍去 \(\mathbf{A}\)

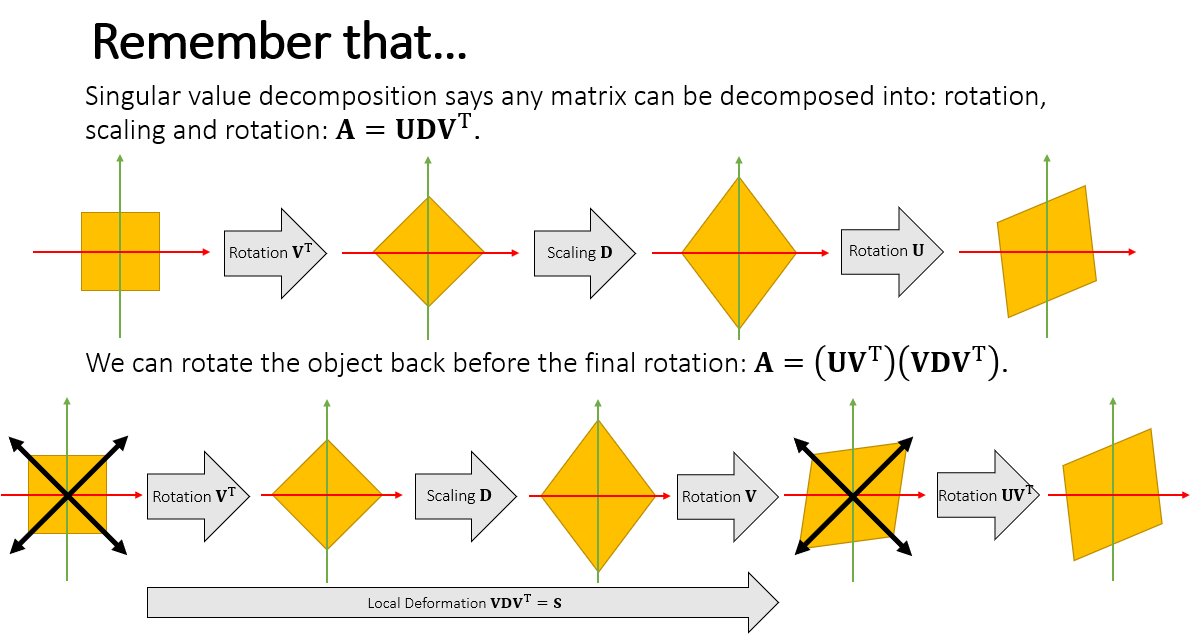
  • polar deformation
    • 直接法求解
      • AN ALGORITHM TO COMPUTE THE SQUARE ROOT OF A 3 X 3 POSITIVE DEFINITE MATRIX
    • 迭代法求解
      • NUMERICAL RECIPES in C - The Art of Scientific Computing

算法流程

  • 每一个顶点都有自己的位置、速度

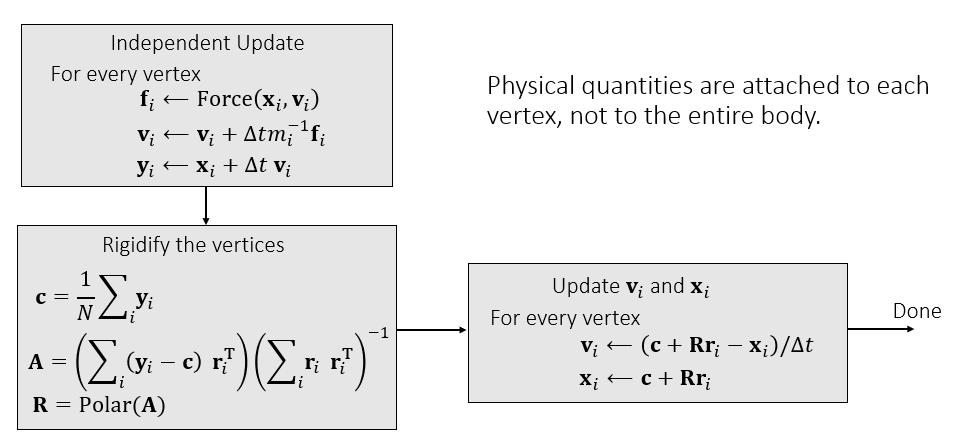
评价

  • 很容易实现
  • 能够很好的模拟其他基于点的系统
    • 布料、软体、粒子的流体
  • 很难严格保证所有的约束都满足
    • 满足一个约束可能会破坏其他约束
    • 可以通过迭代的方式
  • 当摩擦不是很重要的时候，可以使用 shape matching
    • 接触不频繁，例如衣服上的纽扣

论文

  • Muller et al. 2005. Meshless Deformations Based on Shape Matching. TOG (SIGGRAPH).