GAMES103.王华民.03.rigid body dynamic
rigid body dynamics
- 刚体动力学
刚体
- 没有形变
- 现实生活中形变比较小的物体
- 石头、硬币、积木
- 游戏
- 愤怒的小鸟(2D)
- 弹珠
- Unity
- Rigidbody
刚体模拟
- 模拟:根据时间更新物体的状态量
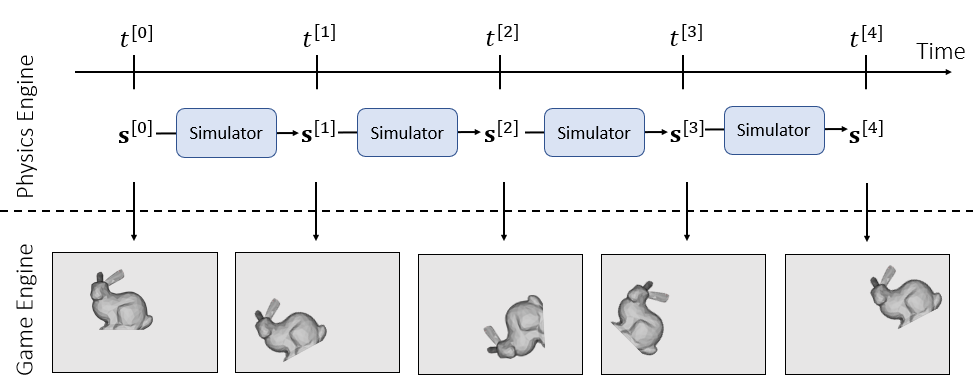
- 怎么描述刚体的状态量
- 刚体只允许两种运动:平移、旋转
- 变换
- 在局部坐标系中旋转,平移到世界坐标系中
- 局部坐标系
- local space
- reference
- 局部坐标系
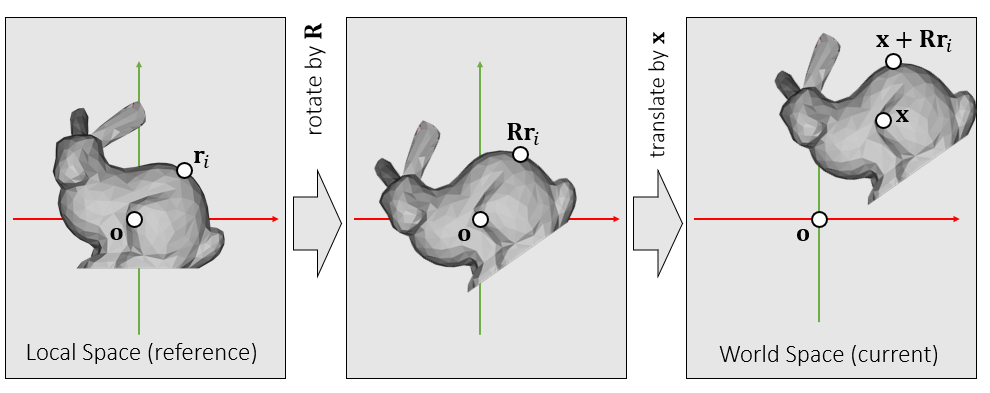
平移变换
- translation motion
- 更新位置 \(\mathbf{x}\)、速度 \(\mathbf{v}=\dot{\mathbf{x}}\)
\[ \begin{aligned} \mathbf{v}(t^{[1]})&=\mathbf{v}(t^{[0]})+M^{-1}\int_{t^{[0]}}^{t^{[1]}}\mathbf{f}(\mathbf{x}(t),\mathbf{v}(t),t)dt\\ \mathbf{x}(t^{[1]})&=\mathbf{x}(t^{[0]})+M^{-1}\int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt\\ \end{aligned} \]
- 求解常微分方程的初值问题
一维示例
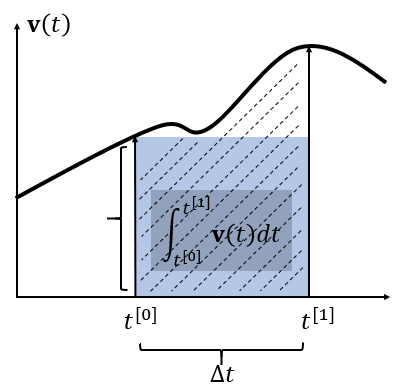
显式欧拉法
- Explicit Euler
- 一阶估计:长方形近似
- 使用 \(t^{[0]}\) 时刻速度估计
\[ \int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt\approx\Delta t\mathbf{v}(t^{[0]}) \]
- 根据泰勒展开,发现这是一阶精确的
- 1st-order accurate
\[ \begin{aligned} \int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt &=\Delta t\mathbf{v}(t^{[0]})+\dfrac{\Delta t^2}{2}\mathbf{v}'(t^{[0]})+\cdots\\ &=\Delta t\mathbf{v}(t^{[0]})+O(\Delta t^2)\\ \end{aligned} \]
隐式欧拉法
- Implicit Euler
- 使用 \(t^{[1]}\) 时刻速度估计
\[ \int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt\approx\Delta t\mathbf{v}(t^{[1]}) \]
- 也是一阶精确的
\[ \begin{aligned} \int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt &=\Delta t\mathbf{v}(t^{[1]})-\dfrac{\Delta t^2}{2}\mathbf{v}'(t^{[1]})+\cdots\\ &=\Delta t\mathbf{v}(t^{[1]})+O(\Delta t^2)\\ \end{aligned} \]
中点法
- Mid-point
- 二阶精确的
\[ \int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt\approx\Delta t\mathbf{v}(t^{[0.5]}) \]
\[ \mathbf{v}(t^{[0.5]})=\dfrac{\mathbf{v}(t^{[0]})+\mathbf{v}(t^{[1]})}{2} \]
- 都在 \(t^{[0.5]}\) 点上进行泰勒展开
\[ \begin{aligned} \int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt =&\int_{t^{[0]}}^{t^{[0.5]}}\mathbf{v}(t)dt+\int_{t^{[0.5]}}^{t^{[1]}}\mathbf{v}(t)dt\\ =&\quad\dfrac{1}{2}\Delta t\mathbf{v}(t^{[0.5]})-\dfrac{\Delta t^2}{4}\mathbf{v}'(t^{[0.5]})+O(\Delta t^3)\\ &+\dfrac{1}{2}\Delta t\mathbf{v}(t^{[0.5]})+\dfrac{\Delta t^2}{4}\mathbf{v}'(t^{[0.5]})+O(\Delta t^3)\\ =&\Delta t\mathbf{v}(t^{[0.5]}))+O(\Delta t^3)\\ \end{aligned} \]
平移变换
- 两个变量
- \(\mathbf{v}\) 使用显式欧拉法,\(\mathbf{x}\) 使用隐式欧拉法
\[ \begin{aligned} \mathbf{v}^{[1]}&=\mathbf{v}^{[0]}+\Delta tM^{-1}\mathbf{f}^{[0]}\\ \mathbf{x}^{[1]}&=\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[1]}\\ \end{aligned} \]
- 也被称为是半欧拉法
- semi-implicit
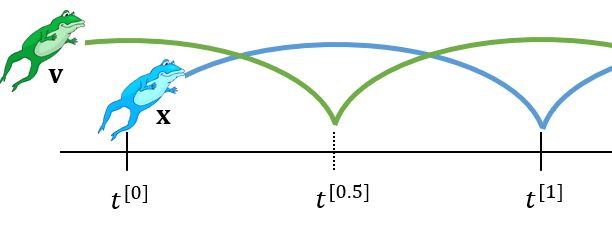
- 本质上是中点法,错开 \(\mathbf{v},\mathbf{x}\)
- 称为是 leapfrog method
\[ \begin{aligned} \mathbf{v}^{[0.5]}&=\mathbf{v}^{[-0.5]}+\Delta tM^{-1}\mathbf{f}^{[0]}\\ \mathbf{x}^{[1]}&=\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0.5]}\\ \end{aligned} \]
- leapfrog
- \(\mathbf{v},\mathbf{x}\) 间隔着更新
力
- 重力
- gravity force
- \(\mathbf{f}^{[0]}_{\mathrm{gravity}}=M\mathbf{g}\)
- 摩擦力(阻力)
- drag force
- \(\mathbf{f}^{[0]}_{\mathrm{drag}}=-\sigma\mathbf{v}^{[0]}\)
- 简单的近似:\(\mathbf{v}^{[1]}=\alpha\mathbf{v}^{[0]}\)
- 直接简单的衰减速度,不精确,但是挺有用的
刚体模拟
- 流程
- 根据当前时刻每一个质点的位置、速度求出每一个质点的力
- 求出合力
- 对整体的速度做更新
- 对整体的位置做更新

- Unity 本身有位置的定义,但是没有定义速度,需要自己定义
旋转变换
- rotational motion
表示方式
- 矩阵、欧拉角、四元数
3x3 矩阵
- 存在冗余性,旋转自由度是 3,而不是 9
- 不直观
- 很难计算时间微分
欧拉角
- Euler Angle
- 直观
- 由 3 个轴的旋转角来定义旋转
- Unity 界面上有这样的定义
- 对时间求微分也比较困难
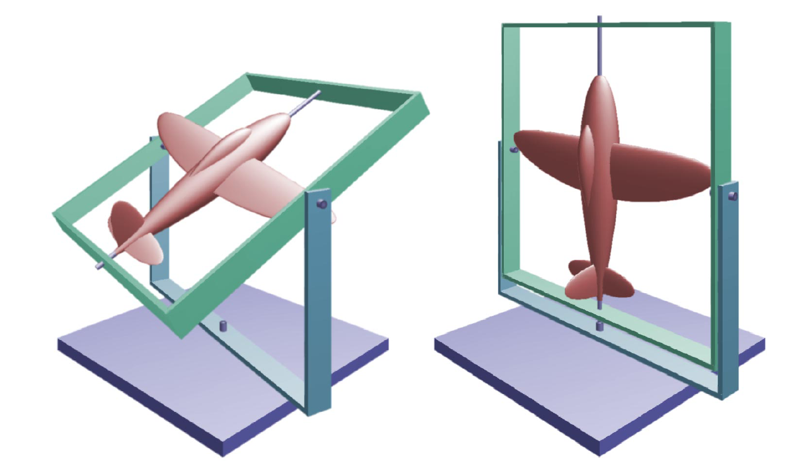
- 万向锁:gimbal lock
- 在某些情况下,自由度减少
- 例如右图,有两个旋转轴重合了
四元数
- 参考
- Quaternion
- 一个复数可以描述二维空间中的点
- 可以定义加减乘除
- 三维空间的点?
- 3d 向量不能定义除法
- 使用类似复数的方式:四元数
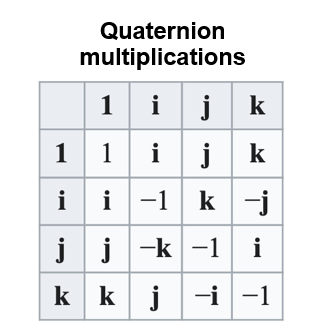
四元数计算法则
- 四元数 \(\mathbf{q}=[s\;\mathbf{v}]\)
- 实数,向量
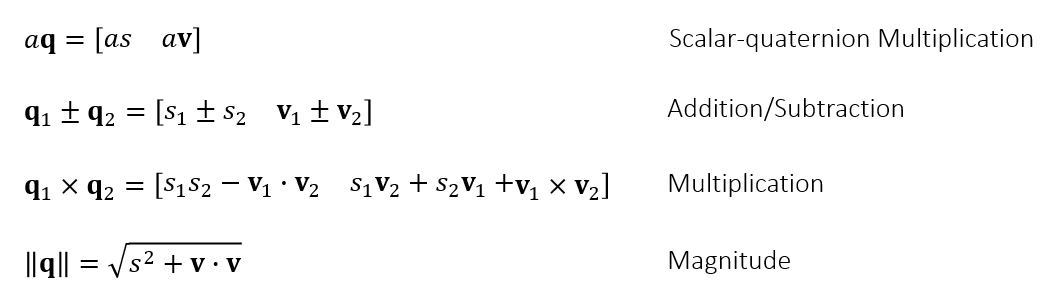
- Unity 里面有四元数,但是只提供了乘法的计算
- \([w,x,y,z]\)
使用四元数表示旋转
- 绕着轴 \(\mathbf{v}\) 旋转 \(\theta\) 角度
- 模长为一限制为单位四元数
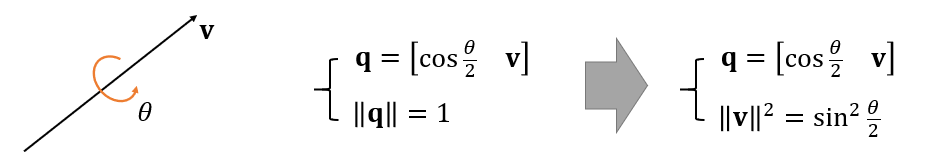
- 很直观,Unity 默认的表达方式
- 转化为矩阵
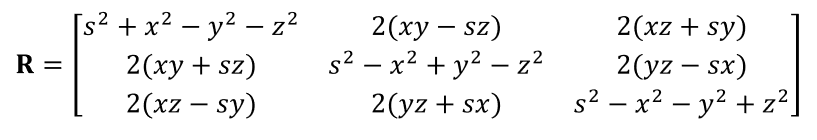
Unity
- 可以通过设置其中的某一个形式的值,从而获取到另一种表达方式的值
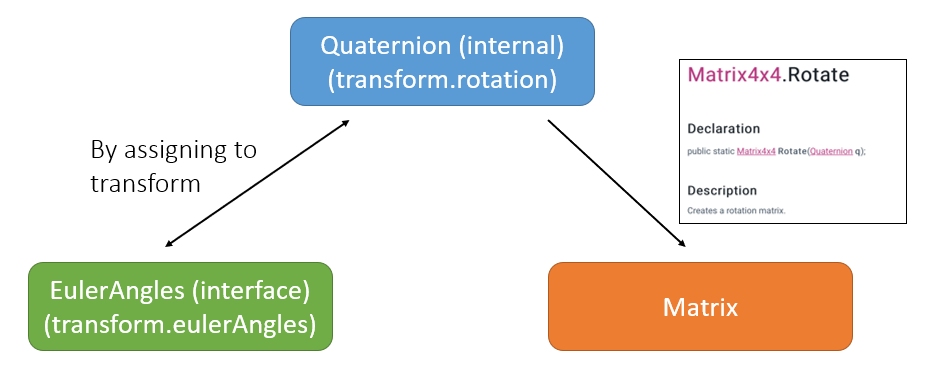
角速度
- 旋转角对于时间求微分
- 使用四元数来表示旋转角(取向 / orientation)
- 使用 3d 向量描述角速度
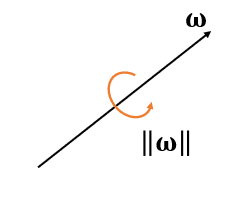
- \(\omega\) 的方向表示旋转方向,\(\omega\) 的大小表示角速度的大小
力矩与转动惯量
- 力矩:torque
- 和力对应,能够让物体产生旋转的趋势
- 转动惯量:inertia
- 和质量对应
更新流程
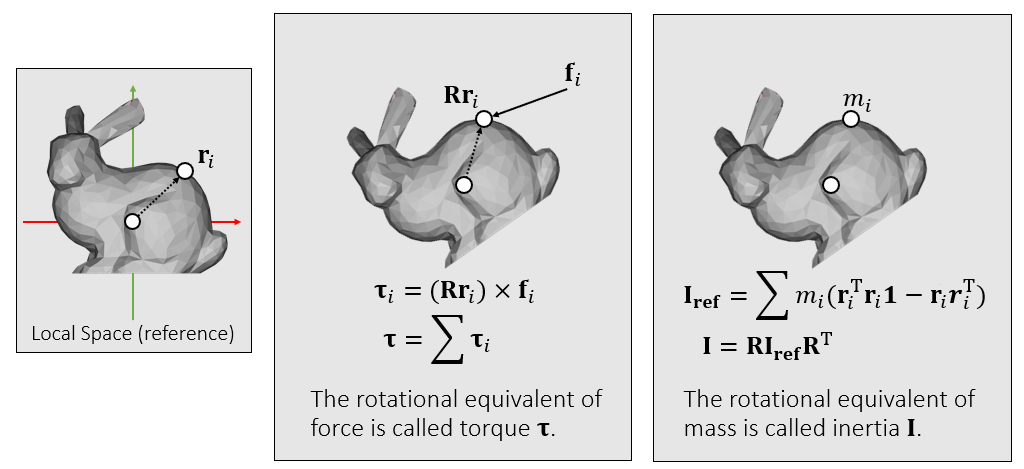
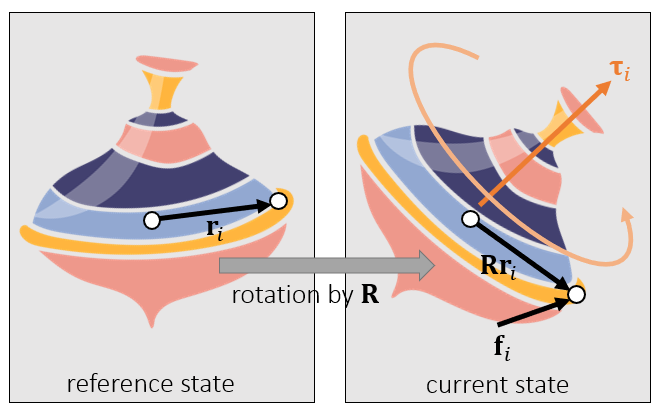
力矩
- 力矩 \(\tau\)
- \(\mathbf{r}_i\):上一时刻的位置
- \(\mathbf{R}\):旋转矩阵
- \(\mathbf{f}_i\):力
- \(\tau=(\mathbf{Rr}_i)\times
\mathbf{f}_i\)
- 和 \(\mathbf{Rr}_i\) 方向一致的时候,不会引发旋转
转动惯量
- 转动惯量 \(\mathbf{I}\)
- 在旋转中等效于质量
- 是一个 3x3 矩阵
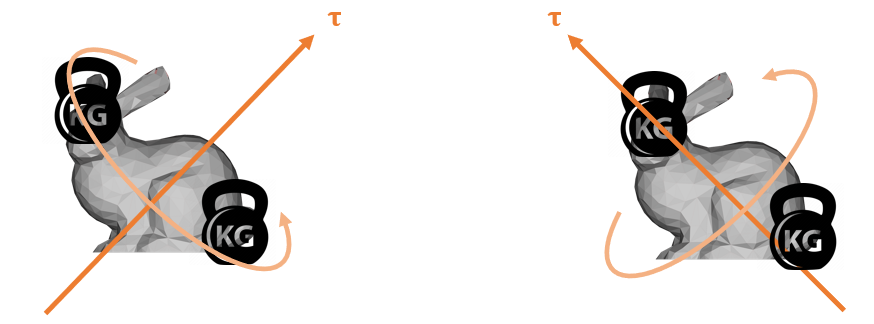
- 为什么是一个矩阵,而不是一个实数?
- 质量抵抗移动,转动惯量抵抗旋转
- 这种抵抗和旋转轴相关
- 如下图
- 左边的抵抗更强
- 右边质量都集中在轴上
- \(\mathbf{I}_{\mathrm{ref}}\) 是固定的,参照状态中的 \(\mathbf{r}_i\) 也是固定的,\(\mathbf{Rr}_i\) 随着时间变化而变化
- 在实际运动中,\(\mathbf{r}_i\) 在变换
- 简化公式
- 只需要计算一次 \(\mathbf{I}_{\mathrm{ref}}\),通过矩阵 \(\mathbf{R}\) 快速计算 \(\mathbf{I}\)
- 不需要每次对所有点求一次
- 注意 \(\mathbf{R}\) 是正交矩阵,\(\mathbf{r}_i^{\mathbf{T}}\mathbf{r}_i\) 是实数,\(\mathbf{1}\) 是 3x3 单位矩阵
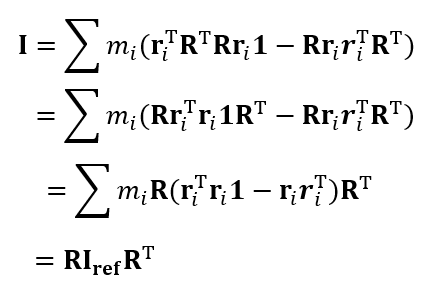
刚体模拟流程
流程
- 模拟平移变换、旋转变换
- 注意 \(\mathbf{q}\) 需要归一化
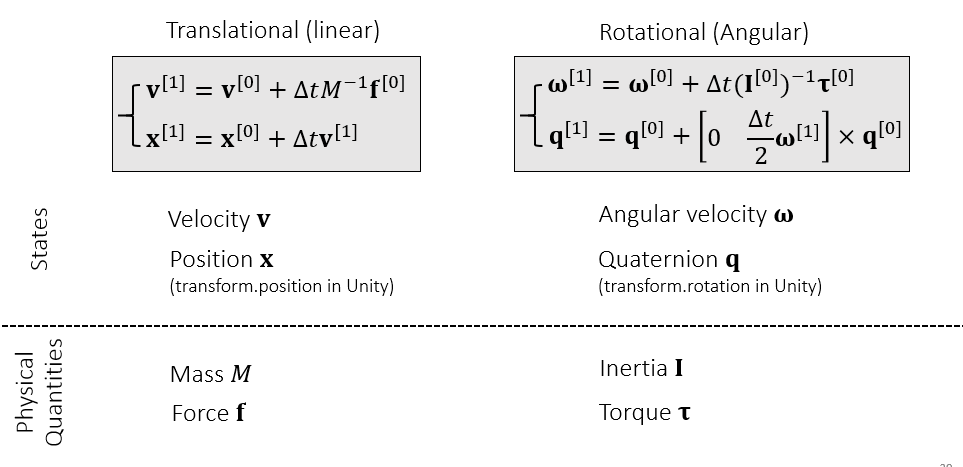
更加细致的流程
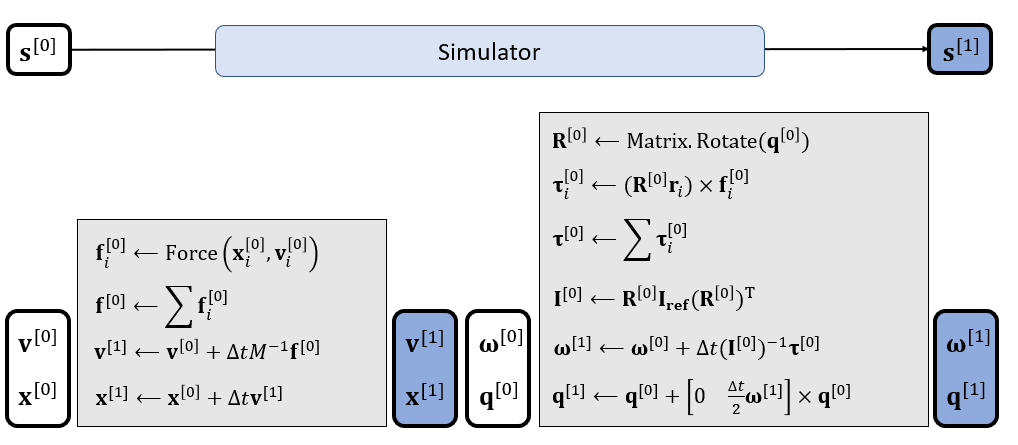
- 最后需要对 \(\mathbf{q}\) 归一化
证明
- \(\dot{\mathbf{q}}=\dfrac{1}{2}[0,\mathrm{\omega}]\mathbf{q}\)
的证明
- 参考
- Appendix B
- \(\mathbf{q}(t)\) 表示如下
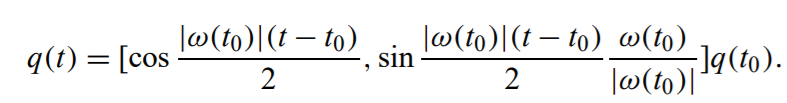
- 求微分即可,计算 \(t=t_0\) 时的值即可
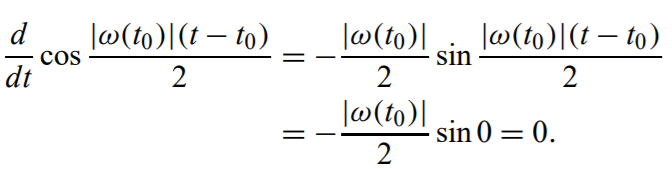
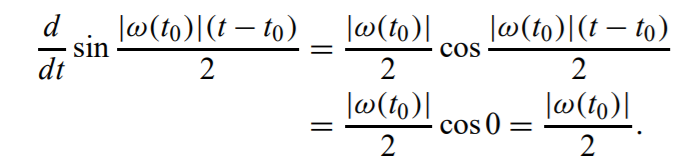
- 代入即得到上面的结果
实现建议
- 平移、旋转分开调试
- 调试旋转的时候,先把 \(\omega\) 设置为常数,看能否旋转
- 重力不会造成力矩
- 自由落体不会自发旋转
- 参考教程
- Rigid Body Dynamics