计算方法B.裴玉茹.08.数值微分与积分(4)
- PPT(数值微分与积分方法)
数值微分与积分方法
1. 数值微分
插值多项式
- 思想:利用拉格朗日插值多项式计算函数导数
- 多项式的导数函数依然是多项式
- 计算简单
- 截断误差构成导数计算的误差
- 方便估计误差
- 多项式的导数函数依然是多项式
- \(n+1\) 点插值多项式
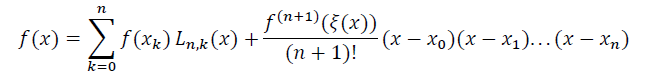
- 求导
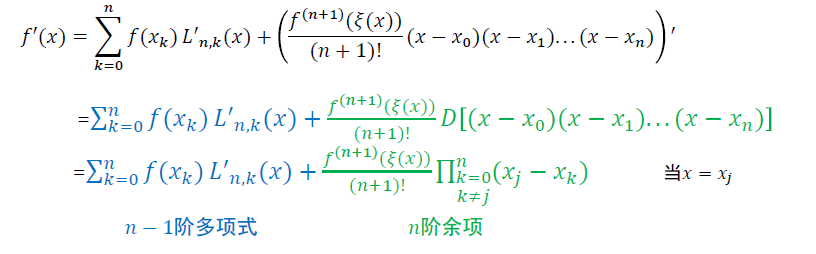
前向差分公式
- 利用泰勒展开的多项式进行近似,忽略高阶项(截断误差)
\[ f'(x)=\dfrac{f(x+h)-f(x)}{h}-\dfrac{h}{2}f''(c),\quad c\in[x,x+h] \]
- 截断误差:\(\dfrac{h}{2}f''(c)\)
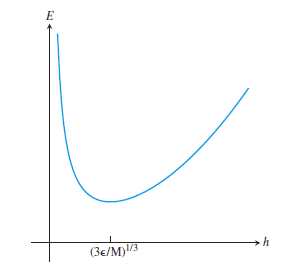
- 舍入误差:\(\dfrac{2\epsilon}{h}\)
三点公式
- 二阶拉格朗日多项式
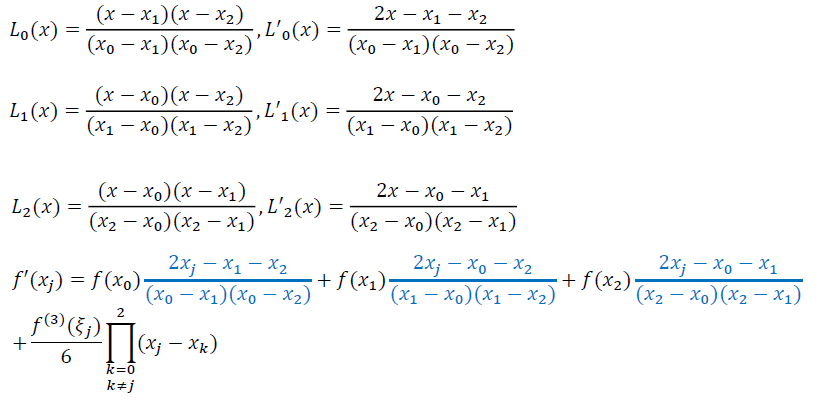
等间距取点
\[ x_2=x_1+h=x_0+2h \]
- \(x_j=x_0\)
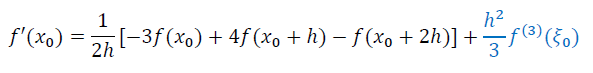
- \(x_j=x_1\)(三点中心差分)
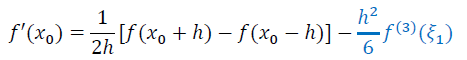
- \(x_j=x_2\)
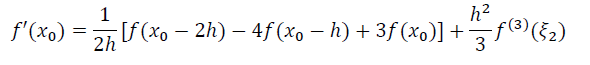
舍入误差与截断误差
- 步长设置
五点公式
- 可以利用三点公式外推得到
- 也可以利用泰勒展开得到
- 泰勒展开
- 先消去偶数次高阶导
- 再消去 3 阶导(\(h\to2h\))
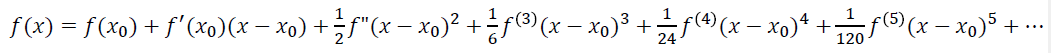
- 五点公式
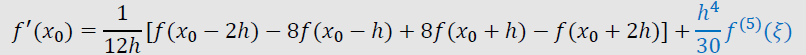
高阶导数计算
- 泰勒展开
\[ f''(x)=\dfrac{f(x+h)+f(x-h)-2f(x)}{h^2}-\dfrac{h^2}{12}f^{(4)}(c),\quad c\in[c-h,c+h] \]
Richardson 外推
- (理查德森)外推
- 使用低阶公式生成高阶公式
- 思路:消去误差最低阶的项
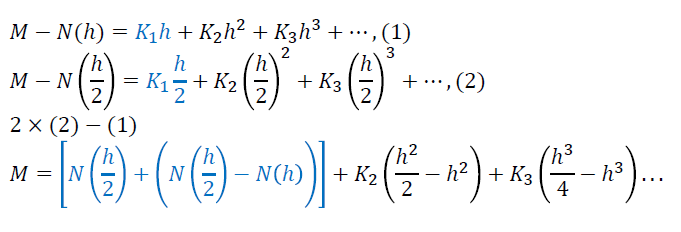
- 可以进一步外推
2. 数值积分
- 思路与之前一致
- 利用拉格朗日插值多项式计算函数积分
- 多项式的积分函数依然是多项式
- 多项式截断误差构成积分计算的截断误差
- 利用拉格朗日插值多项式计算函数积分
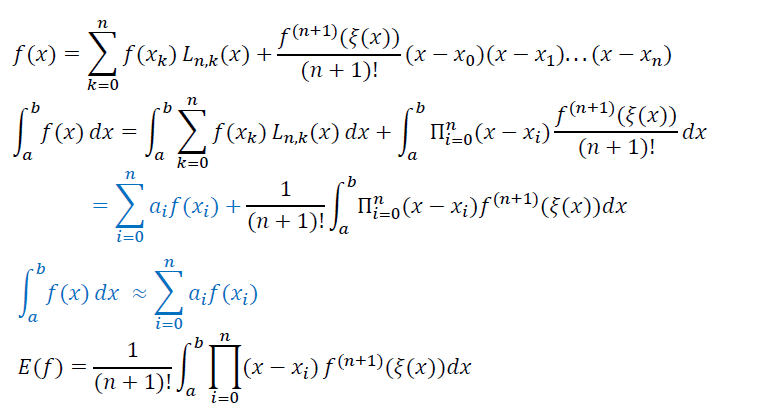
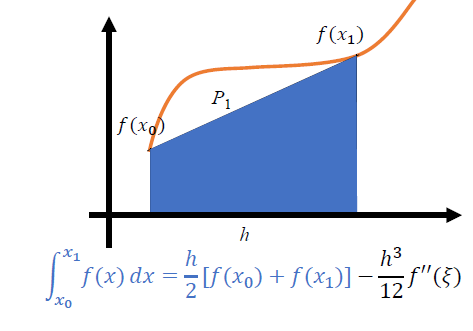
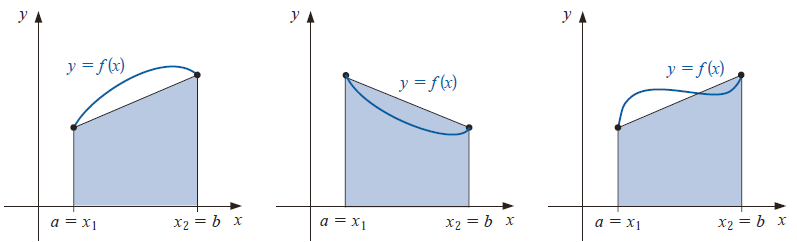
梯形法则
- 一阶多项式插值
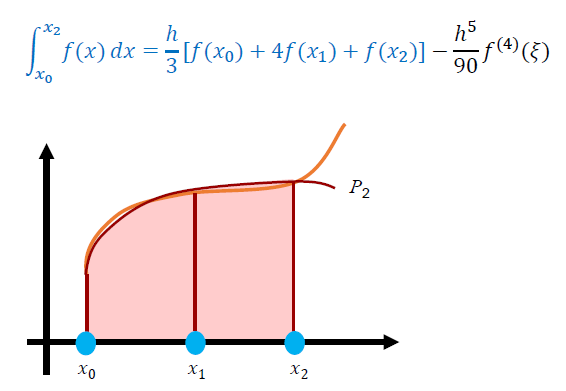
Simpson 法则
- 二阶多项式插值
Newton-Cotes 系数
- 就是从拉格朗日插值多项式推导
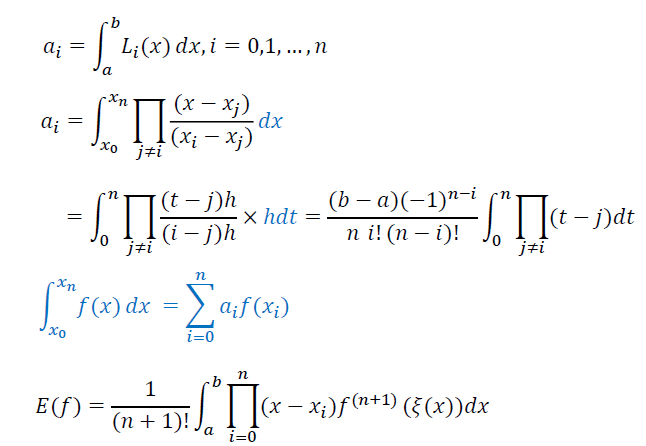
代数精度
- 闭合牛顿-科特斯的代数精度定理

复合数值积分
- 复合梯形、复合辛普森
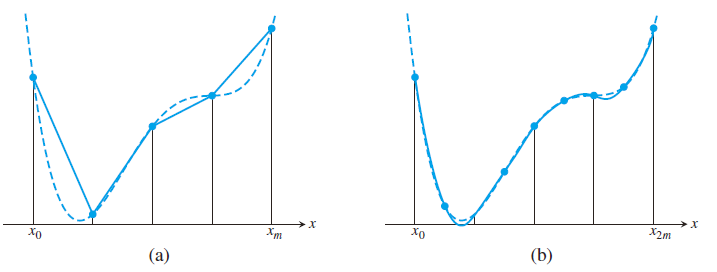
复合梯形
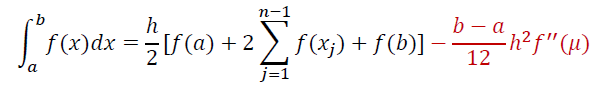
- 舍入误差:\((b-a)\epsilon\)
复合辛普森
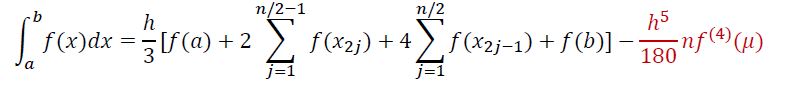
- 舍入误差:\((b-a)\epsilon\)
复合中点
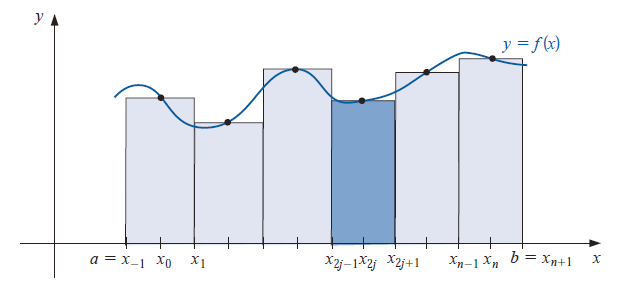
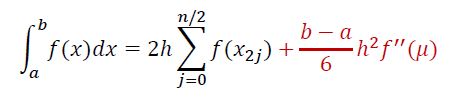
- 舍入误差:\((b-a)\epsilon\)
3. Romberg 积分
- 龙贝格积分
- 复合梯形法则 + 理查德森外推
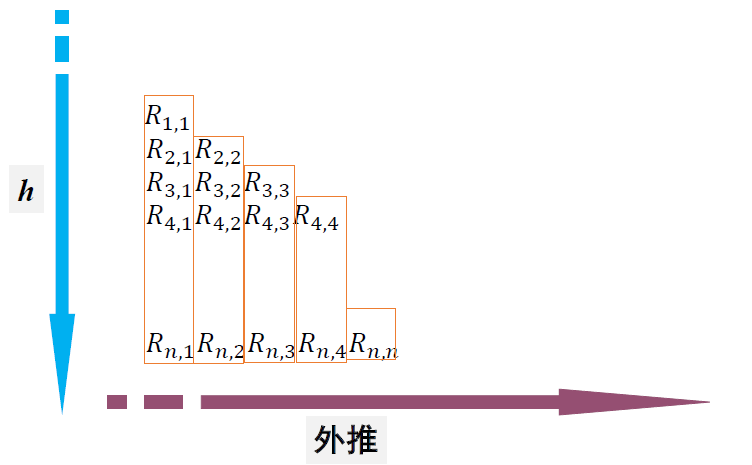
4. 自适应积分
- 动态步长
5. 高斯积分
- 将均匀的节点放置修改为勒让德多项式的根的位置
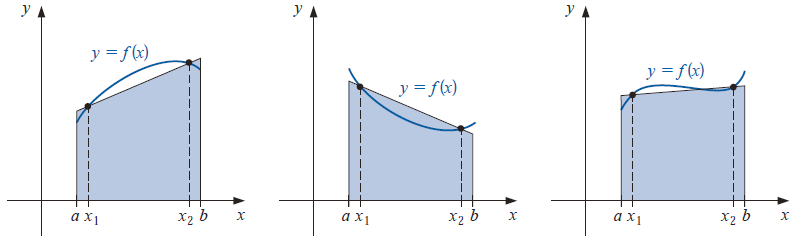
- 代数精度:\(2n-1\)
- 待定系数法找到节点放置位置
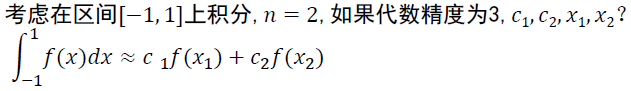
勒让德多项式定理

证明
- 分类:\(p(x)\) 阶数
- \(\deg(p)<n\)
- 插值,直接成立,代入相等
- \(n\le\deg(p)\le2n\)
- 长除法
\[ p(x)=Q(x)P_n(x)+R(x) \]
\[ \int_{-1}^{1}p(x)\mathrm{d}x=\int_{-1}^{1}R(x)\mathrm{d}x=\sum_{i=1}^{n}c_iR(x_i)=\sum_{i=1}^{n}c_ip(x_i) \]
区间变换
- \([a,b]\to[-1,1]\)