计算方法B.裴玉茹.08.数值微分与积分(3)
- 数值分析课本第 5 章(数值微分与积分) + PPT(数值微分与积分方法)
数值微分与积分方法
3. 龙贝格积分
- 为了提高求定积分的精度,我们可以通过添加数据进行扩展
- 龙贝格积分是对复合梯形法则应用外推的结果
- 理查德森外推
- 梯形法则的特殊性,误差没有奇数阶的导数,一次利用外推能够提高两阶精度
- 抵消了
- 梯形法则误差
\[ \int_{a}^{b}f(x)\mathrm{d}x =\dfrac{h}{2}\left(y_0+y_m+2\sum_{i=1}^{m-1}y_{i}\right)+c_2h^2+c_4h^4+\cdots\\ \]
描述
- 需要近似的积分:\(M=\int_{a}^{b}f(x)\mathrm{d}x\)
- 近似公式 \(R_{j,1}\) 表示使用步长为 \(h_j\) 的复合梯形法则,\(h_j\) 定义如下
\[ h_j=\dfrac{b-a}{2^{j-1}} \]
梯形法则
- 给出复合梯形法则的递推形式
- 原始梯形法则
\[ R_{1,1}=\dfrac{h_1}{2}(f(a)+f(b)) \]
- 区间分为等长两段,使用复合梯形法则
\[ \begin{aligned} R_{2,1} &=\dfrac{h_2}{2}\left(f(a)+f(b)+2f(\dfrac{a+b}{2})\right)\\ &=\dfrac{1}{2}R_{1,1}+h_2f(\dfrac{a+b}{2}) \end{aligned} \]
- 归纳证明
\[ R_{j,1}=\dfrac{1}{2}R_{j-1,1}+h_j\sum_{i=1}^{2^{j-2}}f(a+(2i-1)h_j) \]
证明
- 将两个小区间合并为一个大区间
\[ \begin{aligned} R_{j+1,1} &=\dfrac{1}{2}h_{j+1}\sum_{i=1}^{2^{j}}\left(f(a+(i-1)h_{j+1})+f(a+ih_{j+1})\right)\\ &=\dfrac{1}{4}h_{j}\left( \sum_{i=1}^{2^{j-1}}\left(f(a+2(i-1)h_{j+1})+f(a+2ih_{j+1})+2f(a+(2i-1)h_{j+1})\right) \right)\\ &=\dfrac{1}{4}h_{j}\left( \sum_{i=1}^{2^{j-1}}\left(f(a+(i-1)h_{j})+f(a+ih_{j})+2f(a+(2i-1)h_{j+1})\right) \right)\\ &=\dfrac{1}{2}R_{j,1} +\dfrac{1}{4}h_{j}\left( \sum_{i=1}^{2^{j-1}}\left(2f(a+(2i-1)h_{j+1})\right) \right)\\ &=\dfrac{1}{2}R_{j,1} +h_{j+1}\left( \sum_{i=1}^{2^{j-1}}\left(f(a+(2i-1)h_{j+1})\right) \right)\\ \end{aligned} \]
外推
- 第 2 列是第 1 列的外推
- 第 3 列是第 2 列的外推
- \(R_{i,j}\) 是对 \(R_{i-1,j-1}\) 外推的结果

- 根据理查德森外推的形式
\[ Q\approx\dfrac{2^{n}F(h/2)-F(h)}{2^n-1}\\ \]
- 梯形法则精度是 1,是 2 阶近似
\[ R_{2,2}=\dfrac{2^2R_{2,1}-R_{1,1}}{2^2-1}=\dfrac{4^1R_{2,1}-R_{1,1}}{4^1-1} \]
\[ R_{3,3}=\dfrac{2^4R_{3,2}-R_{2,2}}{2^4-1}=\dfrac{4^2R_{2,1}-R_{1,1}}{4^2-1}\\ \]
- 一般化
\[ R_{j,k}=\dfrac{4^{k-1}R_{j,k-1}-R_{j-1,k-1}}{4^{k-1}-1} \]
- 外推结果 \(R_{j,2}\)
是辛普森法则
- 精度为 3,是 4 阶近似
- 可以看看 \(R_{2,2}\) 既是辛普森法则,也是 \(R_{1,1}\) 外推的结果
- 最佳近似 \(R_{j,j}\)
- 何时停止,\(R_{j,j}\) 和 \(R_{j-1,j-1}\) 的差距小于指定值
算法

4. 自适应积分
- 固定步长的问题
- 小步长对应更小的截断误差,对于给定容差我们可以通过误差公式确定步长
\(h\)
- 但是公式中可能包含高阶导数,高阶导数可能无法计算,导致无法确定步长
- 函数变化有的地方很缓,不需要很高的精度,有些地方变化陡,需要较高的精度
- 不同地方精度需求不一致
- 小步长对应更小的截断误差,对于给定容差我们可以通过误差公式确定步长
\(h\)
- 自适应步长
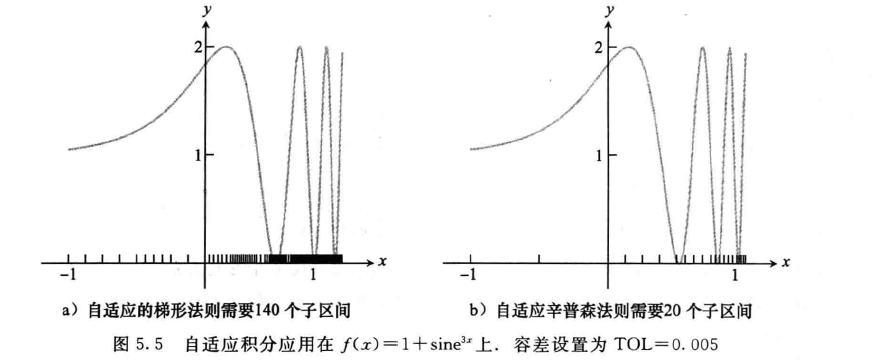
思路
- 我们对当前区间使用梯形法则近似,然后进一步缩短步长,使用两个梯形近似
- 计算这两次计算的误差之差,判断是否可以接受
- 如果可以接受,则结束;如果不能接受,则进一步细分
推导
- 3倍标准

- 定理 5.1:加权中值
算法

高阶自适应积分
- 辛普森法则替换梯形法则
- 15 倍误差

5. 高斯积分
- \(n\) 阶的牛顿-科特斯公式的精度为
\(n\)(\(n\) 为奇数)和 \(n+1\)(\(n\) 为偶数)
- 但是这是均匀分布节点的情况下
- 调整节点的位置,用于提高精度
- 高斯积分精度:\(2n+1\)
正交多项式
\(\int_{a}^{b}p_{i}(x)p_{j}(x)\mathrm{d}x\)
多项式基
- 正交 \(\to\) 线性无关

- 多项式正交集合根定理

勒让德多项式
\[ p_i(x)=\dfrac{1}{2^{i}i!}\dfrac{\mathrm{d}^{i}}{\mathrm{d}x^{i}}[(x^{2}-1)^{i}] \]
- \(p_{i}(x),0\le i\le n\) 在区间 \([-1,1]\) 上正交
- 证明:暴算

高斯积分
- 高斯积分把节点放置在勒让德多项式的根的位置上
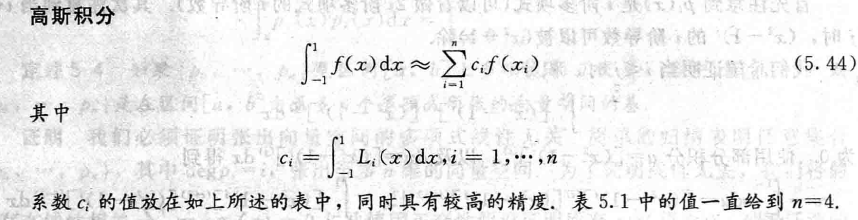
- \(L_i(x)\) 是拉格朗日插值多项式
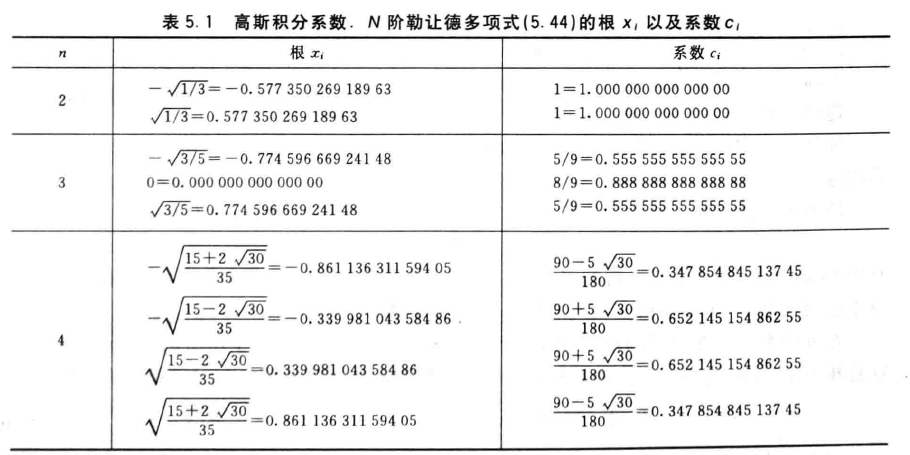
高斯积分的精度
- \(2n-1\)
证明
- 高斯积分的函数记作 \(f(x)\)
- 设 \(P(x)\) 为至多 \(2n-1\) 阶的多项式,那么使用多项式长除法表示
\[ P(x)=S(x)p_n(x)+R(x) \]
- \(p_n(x)\) 为 \(n\) 阶勒让德多项式,\(S(x)\) 和 \(R(x)\) 均为小于 \(n\) 阶的多项式
- 设插值点为 \(x_i(1\le i\le n)\),那么有 \(p_n(x_i)=0\)
- \(P(x_i)=S(x_i)p_n(x_i)+R(x_i)=R(x_i)\)
- 因此高斯积分的插值多项式插值了 \(R(x)\)
- 其实 \(f(x)\) 就是 \(R(x)\)
\[ \int_{-1}^{1}f(x)\mathrm{d}x=\int_{-1}^{1}R(x)\mathrm{d}x \]
- \(S(x)\) 可以表示为 \(n-1\) 阶勒让德多项式集合的线性组合,由正交性
\[ \int_{-1}^{1}S(x)p_n(x)\mathrm{d}x=0 \]
- 那么
\[ \begin{aligned} \int_{-1}^{1}P(x)\mathrm{d}x &=\int_{-1}^{1}S(x)p_n(x)\mathrm{d}x+\int_{-1}^{1}R(x)\mathrm{d}x\\ &=\int_{-1}^{1}R(x)\mathrm{d}x\\ &=\int_{-1}^{1}f(x)\mathrm{d}x \end{aligned} \]
区间变换
- 一般问题积分区间为 \([a,b]\),需要变换到 \([-1,1]\)
\[ \int_{a}^{b}f(x)\mathrm{d}x=\int_{-1}^{1}f(\dfrac{(b-a)t+b+a}{2})\dfrac{b-a}{2}\mathrm{d}t \]