计算方法B.裴玉茹.08.数值微分与积分(2)
- 数值分析课本第 5 章(数值微分与积分) + PPT(数值微分与积分方法)
数值微分与积分方法
2. 数值积分的牛顿-科特斯公式
- 定义在 \([a,b]\) 上的函数 \(f\) 的积分,可以通过以下两种方式求解
- 取区间中的一些点,使用插值多项式近似
- 牛顿-科特斯方法(Newton-Cotes)
- 取区间中的一些点,使用最小二乘多项式近似
- 高斯积分
- 取区间中的一些点,使用插值多项式近似
- 基础积分
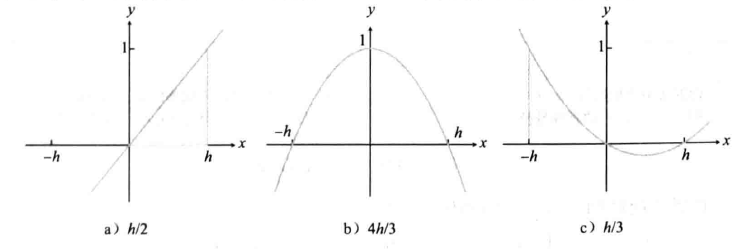
- 插值 \((0,0),(h,1)\) 的直线
\[ \int_{0}^{h}\dfrac{x}{h}\mathrm{d}x=\dfrac{h}{2} \]
- 插值 \((-h,0),(0,1),(h,0)\) 的抛物线 \(P(x)\)
\[ \int_{-h}^{h}P(x)\mathrm{d}x=\int_{0}^{h}\left(-\dfrac{x^2}{h^2}+1\right)\mathrm{d}x=\dfrac{4h}{3} \]
- 插值 \((-h,1),(0,0),(h,0)\) 的抛物线 \(P(x)\)
\[ \int_{-h}^{h}P(x)\mathrm{d}x=\int_{0}^{h}\left(\dfrac{1}{2h^2}x(x-h)\right)\mathrm{d}x=\dfrac{h}{3} \]
2.1 梯形法则
- \(f(x)\) 是定义在 \([x_0,x_1]\) 上的具有连续二阶导数的函数
- 利用通过点 \((x_0,y_0=f(x_0)),(x_1,y_1=f(x_1))\) 的插值多项式进行近似
- 一阶多项式插值
- 拉格朗日插值多项式形式
\[ \begin{aligned} f(x)&=y_0\dfrac{x-x_1}{x_0-x_1}+y_1\dfrac{x-x_0}{x_1-x_0}+\dfrac{(x-x_0)(x-x_1)}{2!}f''(c_x)\\ &=P(x)+E(x)\\ \end{aligned} \]
- 近似积分:\(h=x_1-x_0\)
\[ \int_{x_0}^{x_1}P(x)\mathrm{d}x=y_0\dfrac{h}{2}+y_1\dfrac{h}{2} =\dfrac{(y_0+y_1)h}{2} \]
\[ \int_{x_0}^{x_1}E(x)\mathrm{d}x=-\dfrac{h^3}{12}f''(c) \]
- 梯形法则如下
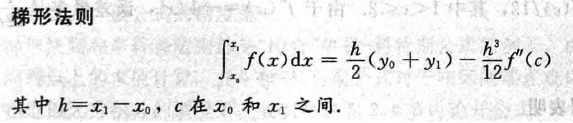
2.2 辛普森法则
- 和梯形法则相比,利用抛物线(二阶多项式)拟合函数,其他和梯形法则相同
- 辛普森法则
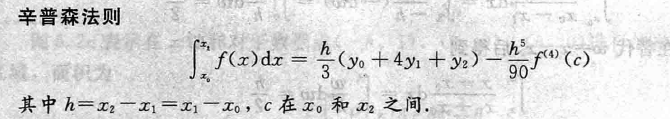
- 过程如下
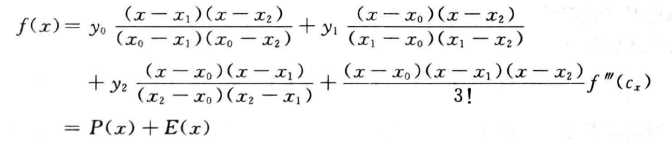
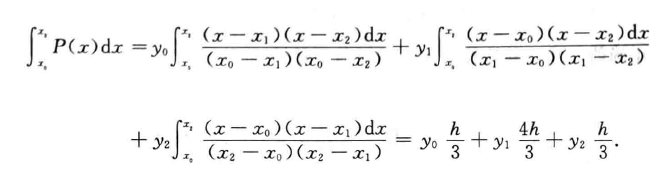
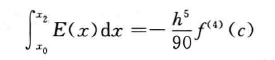
- \(E(x)\) 通过泰勒展开证明
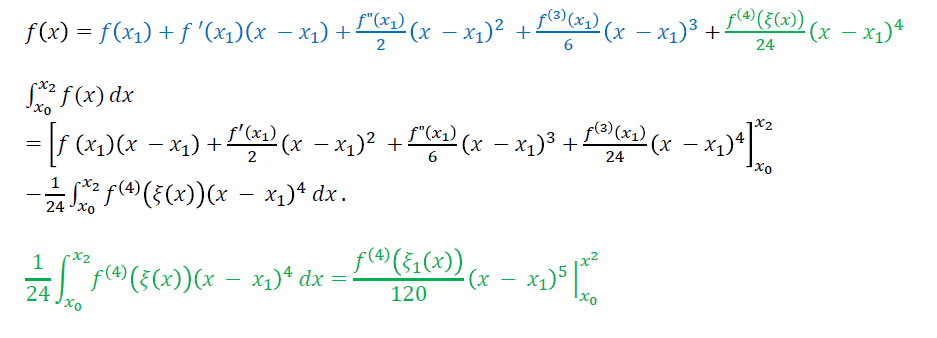
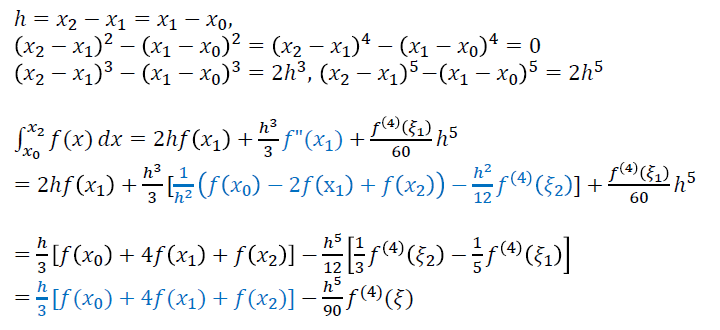
精度
- 数值积分方法的精度是最大的整数 \(k\),使用该积分方法可以得到所有 \(k\) 阶或者更低阶多项式积分的精确值
误差表明精度
- 梯形法则:\(-\dfrac{h^3}{12}f''(c_x)\)
- 精度为 \(1\)
- 辛普森法则:\(\dfrac{h^5}{90}f^{(4)}(c)\)
- 精度为 \(3\)
- 和直觉不太符合,下面一个定理能够加深理解
- 几何解释
- 抛物线和三次样条在三个等间距点上相交,并在相同区间的积分和三次样条的积分一致
辛普森法则的一个定理
- \(P_3(x)\) 是一个三阶多项式,\(P_2(x)\) 是在 \(-h,0,h\) 三个点的插值多项式,那么有
\[ \int_{-h}^{h}P_3(x)\mathrm{d}x=\int_{-h}^{h}P_2(x)\mathrm{d}x \]
- 证明:强行展开即得
- 设 \(P_3(x)\) 如下
\[ P_3(x)=ax^3+bx^2+cx+d \]
- 推导得到 \(P_2(x)\) 如下
\[ P_2(x)=(bx^2+cx+d)+(ah^2x) \]
- 积分相等(奇数次项积分为 0)
辛普森 3/8 公式
- 3 阶牛顿-科特斯公式
\[ \int_{x_0}^{x_3}f(x)\mathrm{d}x\approx\dfrac{3h}{8}(y_0+3y_1+3y_2+y_3) \]
- 验证:只需要测试一系列单项式即可
\[ 1,x,x^2,x^3 \]
- 例如 \(x^3\)
\[ \int_{x_0}^{x_3}x^3\mathrm{d}x=\dfrac{(x_0+3h)^{4}-x_0^4}{4}=\dfrac{3h}{4}(4x_0^{3}+18hx_0^{2}+36h^{2}x_0+27h^{3}) \]
\[ \begin{aligned} &\dfrac{3h}{8}(y_0+3y_1+3y_2+y_3)\\ =&\dfrac{3h}{8}(x_0^3+3(x_0+h)^3+3(x_0+2h)^3+(x_0+3h)^3))\\ =&\dfrac{3h}{8}(8x_0^{3}+36hx_0^{2}+72h^2x_0+54h^3)\\ =&\dfrac{3h}{4}(4x_0^{3}+18hx_0^{2}+36h^{2}x_0+27h^{3}) \end{aligned} \]
- 梯形法则和辛普森法则都是 “闭合” 牛顿-科斯特公式的例子,需要对区间端点求值
- “开” 牛顿-科斯特公式对区间端点难以求值的情况很有用
2.3 复合牛顿-科特斯公式
- 复合数值积分
- 积分在区间的所有子区间上具有可加性
- 把整个区间变为很多小区间再计算积分,在每个小区间上使用法则,然后再求和
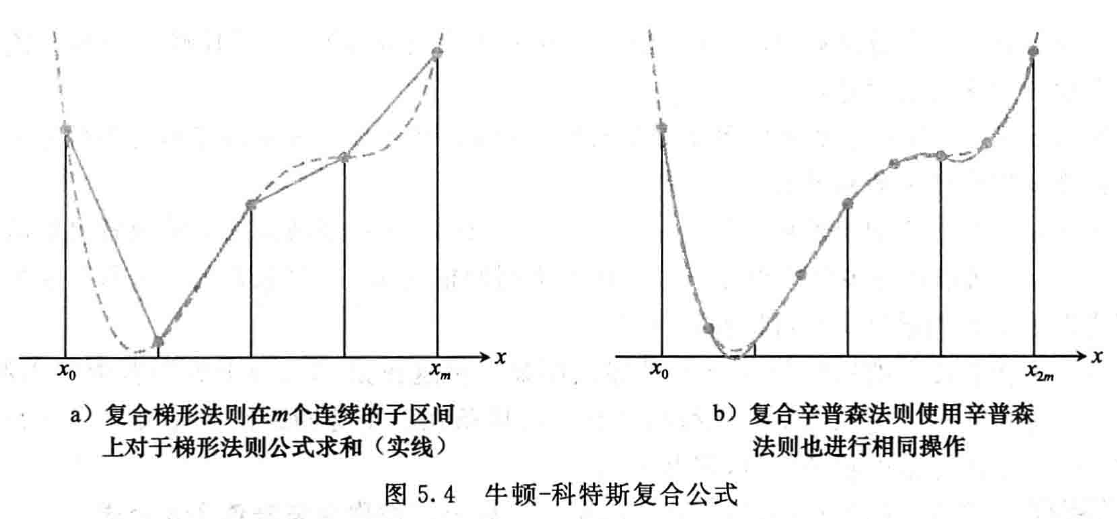
复合梯形法则
- 等长划分某个区间 \([a,b]\)
\[ x_i=x_{i-1}+h,h=\frac{b-a}{m} \]
\[ a=x_0<x_1<\cdots<x_{m-1}<x_m=b \]
- 每个子区间使用梯形法则近似
\[ \int_{x_{i}}^{x_{i+1}}f(x)\mathrm{d}x=\dfrac{h}{2}(f(x_{i})+f(x_{i+1}))-\dfrac{h^3}{12}f''(c_i) \]
- 整个区间
\[ \begin{aligned} \int_{a}^{b}f(x)\mathrm{d}x &=\sum_{i=0}^{m-1}\left(\dfrac{h}{2}(f(x_{i})+f(x_{i+1}))-\dfrac{h^3}{12}f''(c_i)\right)\\ &=\dfrac{h}{2}\left(f(a)+f(b)+2\sum_{i=1}^{m-1}f(x_{i})\right)-\sum_{i=0}^{m-1}\dfrac{h^3}{12}f''(c_i)\\ &=\dfrac{h}{2}\left(f(a)+f(b)+2\sum_{i=1}^{m-1}f(x_{i})\right)-\dfrac{mh^3}{12}f''(c)\\ \end{aligned} \]
- 因此复合梯形法则如下
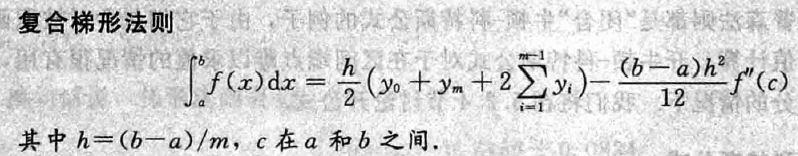
复合辛普森法则
- \([a,b]\) 划分为 \(2m\) 个区间
\[ x_i=x_{i-1}+h,h=\frac{b-a}{2m} \]
\[ a=x_0<x_1<\cdots<x_{2m-1}<x_{2m}=b \]
- 同理我们得到
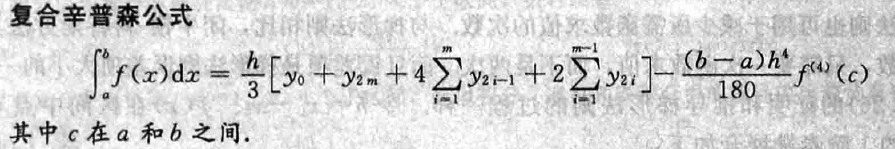
2.4 开牛顿-科特斯方法
- 适用于区间端点的函数值不容易获得的时候
中点法则
- 函数 \(f\) 的二阶导 \(f''(x)\) 在区间 \([a,b]\) 上连续
\[ \int_{x_0}^{x_1}f(x)\mathrm{d}x=hf(w)+\frac{h^3}{24}f''(c) \]
\[ h=x_1-x_0,w=x_0+\dfrac{h}{2} \]
- 证明:在区间中点进行一阶泰勒展开

- 中点法则相较于梯形法则而言
- 函数计算次数变为一半
- 误差界变为一半
复合中点法则
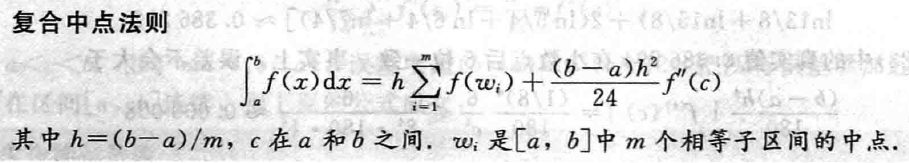
3 阶精度
