计算方法B.裴玉茹.08.数值微分与积分

• 数值分析课本第 5 章（数值微分与积分） + PPT（数值微分与积分方法）

数值微分与积分方法

• 如何计算函数的微分和积分？
  • 符号计算、数值计算
• 如果函数是初等函数，则可以通过符号计算的到结果
• 如果函数表现为采集到的离散点，只能通过数值计算的方法
  • 无法显式表达为初等函数

1. 数值微分

1.1 有限差分公式

• 如果极限存在，则导数定义如下

\[ f'(x)=\lim_{h\to0}\dfrac{f(x+h)-f(x)}{h} \]

• 利用泰勒展开进行近似

二点前向差分公式

• 泰勒展开一阶形式

\[ f(x+h)=f(x)+hf'(x)+\dfrac{h^2}{2}f''(c),\quad c\in[x,x+h] \]

• 二点前向差分公式

\[ f'(x)=\dfrac{f(x+h)-f(x)}{h}-\dfrac{h}{2}f''(c),\quad c\in[x,x+h] \]

• 近似公式，舍去部分作为截断误差

\[ f'(x)\approx\dfrac{f(x+h)-f(x)}{h} \]

• 截断误差 \(O(h)\)
  • 可以通过缩短步长 \(h\) 来减小误差
  • 一阶近似
• 截断误差 \(O(h^n)\)：\(n\) 阶近似

三点中心差分公式

• 泰勒展开二阶形式

\[ \begin{aligned} f(x+h)=f(x)+hf'(x)+\dfrac{h^2}{2}f''(x)+\dfrac{h^3}{6}f^{(3)}(c_1),\quad c_1\in[x,x+h]\\ f(x-h)=f(x)-hf'(x)+\dfrac{h^2}{2}f''(x)-\dfrac{h^3}{6}f^{(3)}(c_2),\quad c_2\in[x,x+h] \end{aligned} \]

• 近似公式

\[ f'(x)=\dfrac{f(x+h)-f(x-h)}{2h}-\dfrac{h^2}{12}\left(f^{(3)}(c_1)+f^{(3)}(c_2)\right) \]

• 根据推广中值定理

• 近似公式进一步可以写作

\[ f'(x)=\dfrac{f(x+h)-f(x-h)}{2h}-\dfrac{h^2}{6}f^{(3)}(c), \quad c\in[x-h,x+h] \]

• 上述式子被称为三点中心差分公式

二阶导数的三点中心差分形式

• 高阶导数的差分形式也可以通过类似方法获得
• 泰勒展开的三阶形式

\[ \begin{aligned} f(x+h)=f(x)+hf'(x)+\dfrac{h^2}{2}f''(x)+\dfrac{h^3}{6}f^{(3)}(x)+\dfrac{h^{4}}{24}f^{(4)}(c_1),\quad c_1\in[x,x+h]\\ f(x-h)=f(x)-hf'(x)+\dfrac{h^2}{2}f''(x)-\dfrac{h^3}{6}f^{(3)}(x)+\dfrac{h^{4}}{24}f^{(4)}(c_2),\quad c_2\in[x,x+h] \end{aligned} \]

• 二阶导数的三点中心差分形式

\[ f''(x)=\dfrac{f(x+h)+f(x-h)-2f(x)}{h^2}-\dfrac{h^2}{12}f^{(4)}(c),\quad c\in[c-h,c+h] \]

1.2 舍入误差

• \(h\) 越小，截断误差越小，但是同时会引入更大的舍入误差
  • 机器精度的原因
  • 两个相近的数相减会导致有效数字丢失、除以一个小数会放大误差

误差分析

• 将 \(f(x+h)\) 的浮点输入记作 \(\hat{f}(x+h)\)，误差近似和机器误差相等

\[ \begin{array}{c} \hat{f}(x+h)=f(x+h)+\epsilon_1\\ \hat{f}(x-h)=f(x-h)+\epsilon_2\\ \vert\epsilon_1\vert,\vert\epsilon_2\vert\approx\vert\epsilon_{\mathrm{mach}}\vert \end{array} \]

• 三点中心差分

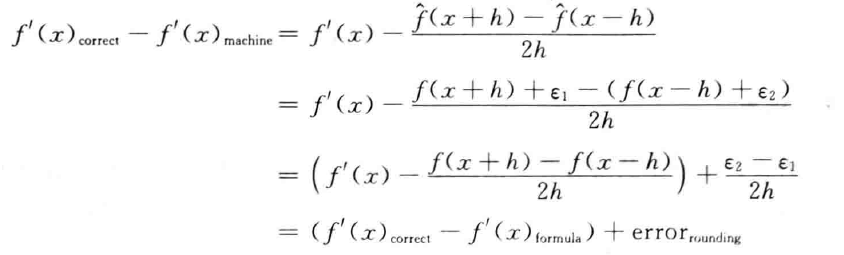
• 两部分误差：截断误差 + 舍入误差
• 舍入误差

\[ \left\vert\dfrac{\epsilon_2-\epsilon_1}{2h}\right\vert\le \dfrac{\epsilon_{\mathrm{mach}}}{h} \]

• 整体误差

\[ E(h)=\dfrac{h^2}{6}f^{(3)}(c)+\dfrac{\epsilon_{\mathrm{mach}}}{h} \]

• 给出最恰当的步长 \(h\)，\(E'(h)=0\)
  • \(M=f^{(3)}(c)\)

\[ h=\sqrt[3]{\dfrac{3\epsilon_{\mathrm{mach}}}{M}} \]

• 可以分析得到步长和误差的关系

1.3 外推

• \(n\) 阶公式 \(F(h)\) 近似一个给定量 \(Q\)，\(n\) 阶含义如下

\[ Q\approx F(h)+Kh^n \]

• 例如上面的三点公式
• 可以通过代数变换的到更高阶的外推
  • 理查德森外推

\[ Q-F(\dfrac{h}{2})\approx K\dfrac{h^n}{2^{n}}\approx\dfrac{Q-F(h)}{2^n{}} \]

\[ Q\approx\dfrac{2^{n}F(h/2)-F(h)}{2^n-1} \]

• 上述式子给出对 \(Q\) 更高阶的近似

• 应用理查德森外推公式，我们可以得到二阶中心差分的更高阶近似

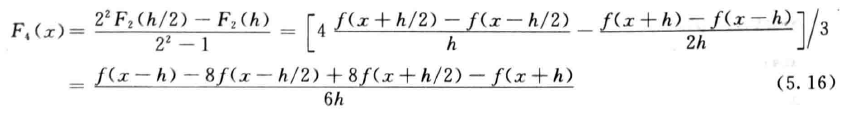
• 这也被称为是五点中心差分公式
  • 上面的讨论论证了这至少是三阶的公式
  • 实际上是四阶的公式
    • 消去了三阶误差项
    • 将 \(f(x+h)\) 展开来为四阶形式，推导即证
• 二阶导数的三点中心差分形式

• 证明

\[ f''(x)=\dfrac{f(x+h)+f(x-h)-2f(x)}{h^2}-\dfrac{h^2}{12}f^{(4)}(x)-\dfrac{h^4}{360}f^{(6)}(c) \]

\[ E_2(x)=\dfrac{h^2}{12}f^{(4)}(x)+\dfrac{h^4}{360}f^{(6)}(c) \]

\[ \begin{aligned} E_4(x) &=\dfrac{ 4\left(\dfrac{h^2}{12\times2^2}f^{(4)}(x)+\dfrac{h^4}{360\times2^4}f^{(6)}(c_1)\right) - \left(\dfrac{h^2}{12}f^{(4)}(x)+\dfrac{h^4}{360}f^{(6)}(c_2)\right) }{3}\\ &=\dfrac{ 4\left(\dfrac{h^4}{360\times2^4}f^{(6)}(c_1)\right) - \left(\dfrac{h^4}{360}f^{(6)}(c_2)\right) }{3}\\ &\approx O(h^4) \end{aligned} \]

1.4 符号微分与积分

• Matlab 中集成了这个功能

• 好强，牛逼