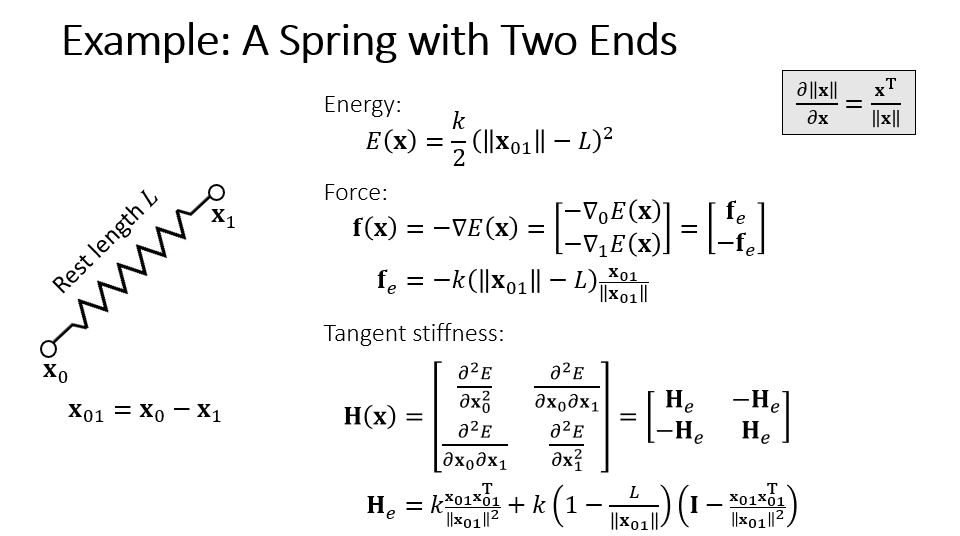GAMES103.王华民.02.Math Background(3)
Math Background
Tensor Calculus
- 张量微积分
一阶导
实数对向量求导
- \(f(\mathbf{x})\in\mathbb{R}\)
\[ \begin{aligned} df&=\dfrac{\partial{f}}{\partial{x}}dx+\dfrac{\partial{f}}{\partial{y}}dy+\dfrac{\partial{f}}{\partial{z}}dz\\ &= \begin{bmatrix} \dfrac{\partial{f}}{\partial{x}}& \dfrac{\partial{f}}{\partial{y}}& \dfrac{\partial{f}}{\partial{z}} \end{bmatrix} \begin{bmatrix} dx\\dy\\dz\\ \end{bmatrix} \end{aligned} \]
- 记号
\[ \dfrac{\partial{f}}{\partial{\mathbf{x}}}= \begin{bmatrix} \dfrac{\partial{f}}{\partial{x}}& \dfrac{\partial{f}}{\partial{y}}& \dfrac{\partial{f}}{\partial{z}} \end{bmatrix} \]
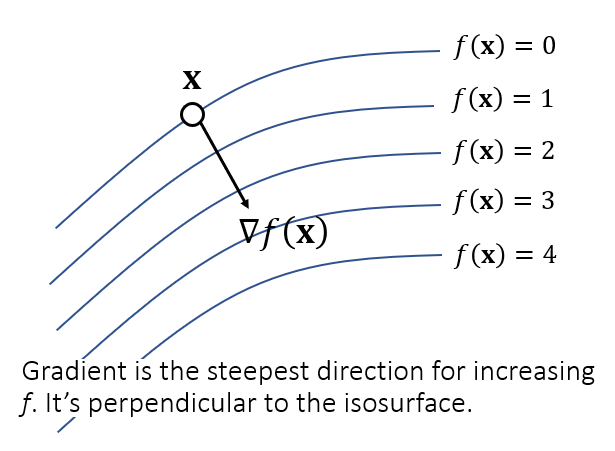
- 梯度(gradient)
\[ \nabla{f(\mathbf{x})}= \begin{bmatrix} \dfrac{\partial{f}}{\partial{x}}\\ \dfrac{\partial{f}}{\partial{y}}\\ \dfrac{\partial{f}}{\partial{z}} \end{bmatrix} \]
- 梯度的方向:函数值上升最快的方向
向量对向量求导
\[ \mathbf{f}(\mathbf{x})= \begin{bmatrix} f(\mathbf{x})\\ g(\mathbf{x})\\ h(\mathbf{x})\\ \end{bmatrix} \in\mathbb{R}^3 \]
- 雅可比矩阵(Jacobian)
\[ \mathbf{J}(x) =\dfrac{\partial{\mathbf{f}}}{\partial{\mathbf{x}}} =\begin{bmatrix} \dfrac{\partial{f}}{\partial{x}}& \dfrac{\partial{f}}{\partial{y}}& \dfrac{\partial{f}}{\partial{z}}\\ \dfrac{\partial{g}}{\partial{x}}& \dfrac{\partial{g}}{\partial{y}}& \dfrac{\partial{g}}{\partial{z}}\\ \dfrac{\partial{h}}{\partial{x}}& \dfrac{\partial{h}}{\partial{y}}& \dfrac{\partial{h}}{\partial{z}} \end{bmatrix} \]
- 散度(Divergence):雅可比矩阵对角和
\[ \nabla\cdot{\mathbf{f}}=\dfrac{\partial{f}}{\partial{x}}+\dfrac{\partial{g}}{\partial{y}}+\dfrac{\partial{h}}{\partial{z}} \]
- 旋度(Curl)
\[ \nabla\times\mathbf{f}=\begin{bmatrix} \dfrac{\partial{h}}{\partial{y}}-\dfrac{\partial{g}}{\partial{z}}\\ \dfrac{\partial{f}}{\partial{z}}-\dfrac{\partial{h}}{\partial{x}}\\ \dfrac{\partial{g}}{\partial{x}}-\dfrac{\partial{f}}{\partial{y}}\\ \end{bmatrix} \]
- 把 \(\nabla\) 当作算子
\[ \nabla=\begin{bmatrix} \dfrac{\partial}{\partial{x}}&\dfrac{\partial}{\partial{y}}&\dfrac{\partial}{\partial{z}} \end{bmatrix} \]
二阶导
实数对向量求导
- 海森矩阵(Hessian)
- 求导顺序不影响结果
\[ \mathbf{H}=\mathbf{J}(\nabla f(\mathbf{x}))=\begin{bmatrix} \dfrac{\partial^2{f}}{\partial^2{x}} &\dfrac{\partial^2{f}}{\partial{x}\partial{y}} &\dfrac{\partial^2{f}}{\partial{x}\partial{z}}\\ \dfrac{\partial^2{f}}{\partial{x}\partial{y}} &\dfrac{\partial^2{f}}{\partial^2{y}} &\dfrac{\partial^2{f}}{\partial{y}\partial{z}}\\ \dfrac{\partial^2{f}}{\partial{x}\partial{z}} &\dfrac{\partial^2{f}}{\partial{y}\partial{z}} &\dfrac{\partial^2{f}}{\partial^2{z}}\\ \end{bmatrix} \]
- 拉普拉斯(Laplacian)
- 海森矩阵对角线的和
\[ \nabla\cdot\nabla f(\mathbf{x})=\nabla^2f(\mathbf{x})=\Delta f(\mathbf{x}) =\dfrac{\partial^2{f}}{\partial^2{x}} +\dfrac{\partial^2{f}}{\partial^2{y}} +\dfrac{\partial^2{f}}{\partial^2{z}} \]
泰勒展开
- \(f(x)\in\mathbb{R}\)
\[ f(x)=f(x_0)+\dfrac{\partial{f(x_0)}}{\partial{x}}(x-x_0)+\dfrac{1}{2}\dfrac{\partial^2{f(x_0)}}{\partial^2{x}}(x-x_0)^2+\cdots \]
- \(f(\mathbf{x})\in\mathbb{R}\)
\[ \begin{aligned} f(\mathbf{x})&=f(\mathbf{x}_0)+\dfrac{\partial{f(\mathbf{x}_0)}}{\partial{\mathbf{x}}}(\mathbf{x}-\mathbf{x}_0)+\dfrac{1}{2}\dfrac{\partial^2{f(\mathbf{x}_0)}}{\partial^2{\mathbf{x}}}+\cdots\\ &=f(\mathbf{x}_0) +\nabla f(\mathbf{x}_0)(\mathbf{x}-\mathbf{x}_0) +\dfrac{1}{2}(\mathbf{x}-\mathbf{x}_0)^{\mathbf{T}}\mathbf{H}(\mathbf{x}-\mathbf{x}_0)+\cdots\\ \end{aligned} \]
计算向量范数的偏导
\[ \begin{aligned} \dfrac{\partial{\Vert{\mathbf{x}}\Vert}}{\partial{\mathbf{x}}} &=\dfrac{\partial({\mathbf{x}^{\mathbf{T}}\mathbf{x}})^{1/2}}{\partial{\mathbf{x}}}\\ &=\dfrac{1}{2}({\mathbf{x}^{\mathbf{T}}\mathbf{x}})^{-1/2}\dfrac{\partial({\mathbf{x}^{\mathbf{T}}\mathbf{x}})}{\partial{\mathbf{x}}}\\ &=\dfrac{1}{2}({\mathbf{x}^{\mathbf{T}}\mathbf{x}})^{-1/2}\cdot2\mathbf{x}^{\mathbf{T}}\\ &=\dfrac{\mathbf{x}^{\mathbf{T}}}{\Vert{\mathbf{x}}\Vert}\\ \end{aligned} \]
- 结论
\[ \dfrac{\partial{\Vert{\mathbf{x}}\Vert}}{\partial{\mathbf{x}}} =\dfrac{\mathbf{x}^{\mathbf{T}}}{\Vert{\mathbf{x}}\Vert}\\ \]
- 细节
\[ \dfrac{\partial({\mathbf{x}^{\mathbf{T}}\mathbf{x}})}{\partial{\mathbf{x}}} =\dfrac{\partial(x^2+y^2+z^2)}{\partial{\mathbf{x}}} =\begin{bmatrix} 2x&2y&2z \end{bmatrix} =2\mathbf{x}^{\mathbf{T}} \]
- 直观理解:长度变长的最快方向就是自身方向
例子:弹簧
- Choi and Ko. 2002. Stable But Responive Cloth. TOG (SIGGRAPH)
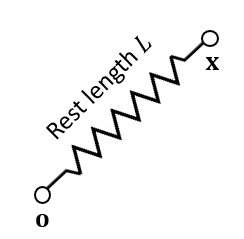
- 弹簧能量
- Energy
\[ E(\mathbf{x})=\dfrac{k}{2}(\Vert\mathbf{x}\Vert-L)^{2} \]
- 弹簧力(物理推导)
- Force
\[ \begin{aligned} \mathbf{f}(\mathbf{x})&=-\nabla E(\mathbf{x})\\ &=-k(\Vert\mathbf{x}\Vert-L)\left(\dfrac{\partial{\Vert{\mathbf{x}}\Vert}}{\partial{\mathbf{x}}}\right)^{\mathbf{T}}\\ &=-k(\Vert\mathbf{x}\Vert-L)\dfrac{\mathbf{x}}{\Vert{\mathbf{x}}\Vert} \end{aligned} \]
- Hessian
- Tangent stiffness
- 曲面二阶导
- \(\mathbf{x}\) 是一维,那么就是 \(k\)
- Tangent stiffness
\[ \begin{aligned} \mathbf{H}(\mathbf{x})&=-\dfrac{\partial f(\mathbf{x})}{\partial\mathbf{x}}\\ &=k\left( \dfrac{\mathbf{x}\mathbf{x}^{\mathbf{T}}}{\Vert{\mathbf{x}}\Vert^2} +(\Vert\mathbf{x}\Vert-L)\left( \dfrac{\mathbf{I}}{\Vert{\mathbf{x}}\Vert}-\dfrac{\mathbf{x}}{\Vert{\mathbf{x}}\Vert^2}\dfrac{\mathbf{x}^{\mathbf{T}}}{\Vert{\mathbf{x}}\Vert} \right)\right)\\ &=k\left( \dfrac{\mathbf{x}\mathbf{x}^{\mathbf{T}}}{\Vert{\mathbf{x}}\Vert^2} +(1-\dfrac{L}{\Vert\mathbf{x}\Vert})\left( \mathbf{I}-\dfrac{\mathbf{x}\mathbf{x}^{\mathbf{T}}}{\Vert{\mathbf{x}}\Vert^2} \right)\right)\\ \end{aligned} \]
- 两个点都是活动点
- \(\mathbf{x}\) 是 6 维的,两个点的位置