GAMES103.王华民.02.Math Background(2)

Posted on Edited on In Views:
矩阵、矩阵基本操作、奇异值分解、特征值分解、对称正定性、线性方程组求解

Math Background

Matrices

  • 图形学中常见的 \(4\times4,3\times3\) 的矩阵

基本操作

  • 转置：transpose
  • 对称矩阵：symmetric
    • \(\mathbf{A}^{\mathbf{T}}=\mathbf{A}\)
  • 对角矩阵：diagonal
  • 单位矩阵：identity
    • \(\mathbf{I}\)
  • 乘法
    • 矩阵 乘 向量
    • 矩阵 乘 矩阵
      • 满足结合律，一般不满足交换律

\[ (\mathbf{AB})^{\mathbf{T}}=\mathbf{B}^{\mathbf{T}}\mathbf{A}^{\mathbf{T}} \]

\[ (\mathbf{A}\mathbf{A}^{\mathbf{T}})^{\mathbf{T}}=\mathbf{A}\mathbf{A}^{\mathbf{T}} \]

\[ (\mathbf{A}+\mathbf{A}^{\mathbf{T}})^{\mathbf{T}}=\mathbf{A}+\mathbf{A}^{\mathbf{T}} \]

  • 求逆

\[ \mathbf{A}\mathbf{A}^{-1}=\mathbf{I} \]

\[ (\mathbf{AB})^{-1}=\mathbf{B}^{-1}\mathbf{A}^{-1} \]

  • 正交矩阵

\[ \mathbf{A}\mathbf{A}^{\mathbf{T}}=\mathbf{I} \]

\[ \mathbf{A}^{-1}=\mathbf{A}^{\mathbf{T}} \]

  • 旋转变换：正交矩阵
    • 旋转矩阵就是新的 \(xyz\) 轴在原来坐标系中对应的位置组成的矩阵

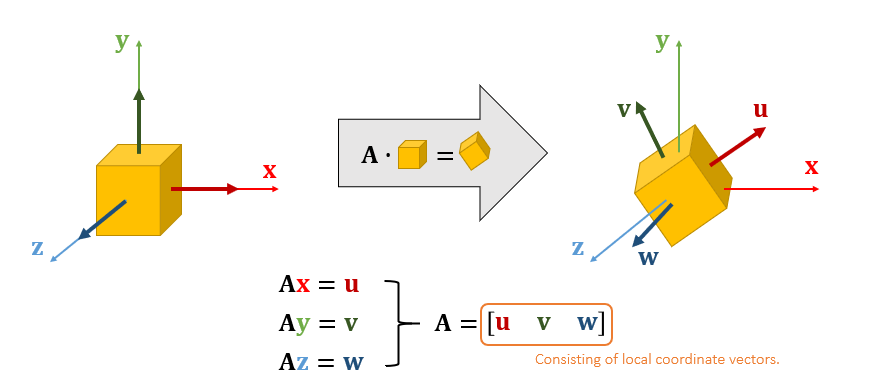
  • 放缩变换

奇异值分解

  • SVD
    • Singular Value Decomposition
  • 任意矩阵的奇异值分解
    • 对角矩阵 \(\mathbf{D}\)
    • 正交矩阵 \(\mathbf{U},\mathbf{V}\)

\[ \mathbf{A}=\mathbf{U}\mathbf{D}\mathbf{V}^{\mathbf{T}} \]

  • 图形学中的某个解释
  • 任何线性变换都可以通过如下三步实现
    • 旋转 \(\mathbf{V}^{\mathbf{T}}\)、缩放 \(\mathbf{D}\)、旋转 \(\mathbf{U}\)

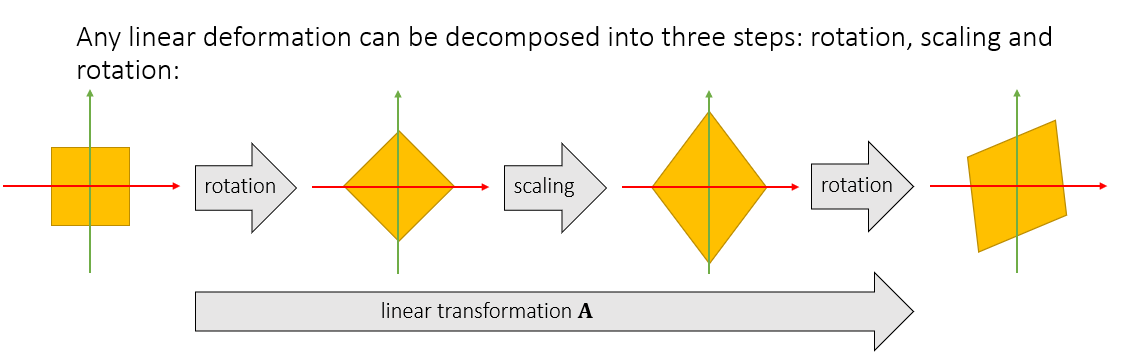
特征值分解

  • 对称矩阵的特征值分解

    • 对角矩阵 \(\mathbf{D}\)

    • 正交矩阵 \(\mathbf{U}\)

\[ \mathbf{A}=\mathbf{U}\mathbf{D}\mathbf{U}^{\mathbf{T}} \]

  • \(\mathbf{D}\) 的对角元素为特征值，\(\mathbf{U}\) 的列向量为特征向量

\[ \mathbf{A}\mathbf{u}_i=\mathbf{U}\mathbf{D}\mathbf{U}^{\mathbf{T}}\mathbf{u}_i=d_i\mathbf{u}_i \]

  • 图形学中大多考虑的都是对称矩阵
    • 非对称矩阵特征值可能会有虚数，图形学中不考虑虚数

对称正定矩阵

  • Symmetric Position Definiteness
    • s.p.d.
  • 对称正定：\(\mathbf{v}^{\mathbf{T}}\mathbf{A}\mathbf{v}>0\)
  • 对称半正定：\(\mathbf{v}^{\mathbf{T}}\mathbf{A}\mathbf{v}\ge0\)
  • 对称正定 \(\Longleftrightarrow\) 特征值都大于 0
  • 对角占优矩阵 \(\Longrightarrow\) 正定的（不一定是对称的）
    • 每一行中，对角元素的绝对值大于剩余元素绝对值之和
  • 对称正定矩阵一定是可逆的

\[ \mathbf{A}^{-1}=\mathbf{U}\mathbf{D}^{-1}\mathbf{U}^{\mathbf{T}} \]

Quiz

  • \(\mathbf{A}\) 是对称正定的，证明 \(\mathbf{B}\) 是对称半正定的

\[ \mathbf{B}= \begin{bmatrix} -\mathbf{A}&\mathbf{A}\\ \mathbf{A}&-\mathbf{A}\\ \end{bmatrix} \]

  • 定义出发证明即可

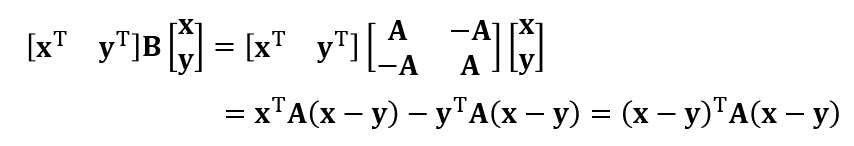
  • 在物理模拟中经常遇到这样的矩阵，比较重要的性质

线性方程组求解问题

\[ \mathbf{A}{\color{red}\mathbf{x}}=\mathbf{b} \]

  • 方阵 \(\mathbf{A}\)
    • square matrix
  • 边界条件 \(\mathbf{b}\)
    • boundary vector
  • \(\mathbf{x}=\mathbf{A}^{-1}\mathbf{b}\)
    • \(\mathbf{A}^{-1}\) 很难计算
    • 带来计算问题、存储问题
      • 稀疏矩阵 \(\mathbf{A}\) 可以优化存储，但是它的逆不稀疏

LU 分解

  • 直接法求解线性方程组

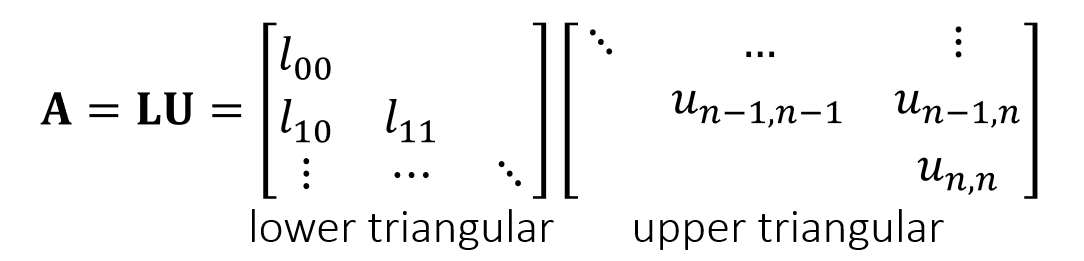
  • LU 分解之后，求解矩阵的开销从 \(O(n^3)\) 变成 \(O(n^2)\)
特点
  • 如果 \(\mathbf{A}\) 是稀疏的，\(\mathbf{L},\mathbf{U}\) 则没有那么稀疏
    • 可以通过改变行列的顺序让 \(\mathbf{L},\mathbf{U}\) 的稀疏性变好
    • 在进行 LU 分解之前会进行 permutation（重排行列）
  • 计算分为两步
    • 第一步分解 \(O(n^3)\)
      • 如果 \(\mathbf{A}\) 固定，则只需要做一次
    • 第二步求解 \(O(n^2)\)
  • 难以并行

迭代方法求解

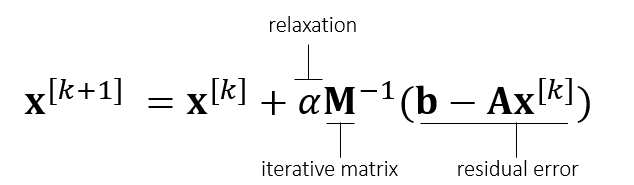
  • \(\mathbf{I}-\alpha\mathbf{A}\mathbf{M}^{-1}\) 的谱半径小于 1 时收敛
    • spectral radius
  • \(\mathbf{M}\) 需要容易计算
    • 雅可比方法：\(\mathbf{M}=\mathbf{I}\)
    • 高斯赛德尔方法：\(\mathbf{M}=\mathrm{lower}(\mathbf{A})\)
  • 共轭梯度法
  • 切比雪夫加速
特点
  • 好处
    • 简单
    • 不需要精确解的情况下，求解比较快
    • 容易并行
  • 缺点
    • 存在收敛性问题
      • 在某些情况下是能够保证收敛的
    • 求精确解可能比较慢