GAMES103.王华民.02.Math Background

Posted on Edited on In Views:
向量、向量计算、向量计算在图形学中应用示例

Math Background

  • 数学预备知识介绍
  • Vector, Matrix and Tensor Calculus
    • 向量、矩阵、张量微积分

Vectors

Geometry Vector

  • 矢量的定义（有几何含义）
  • An (Euclidean) vector
    • A geometric entity endowed with magnitude and direction
  • 向量（矢量）
    • 带有大小和方向的量
  • 论文中区分标量和矢量
    • 矢量：黑体 \(\mathbf{p}\)
    • 标量：斜体 \(p\)
    • 矩阵：大写 \(\mathbf{M}\)

坐标系

  • 右手系、左手系

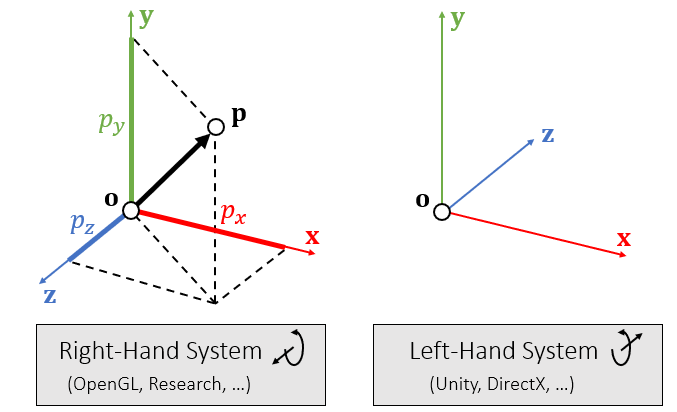
  • 左手系的好处
    • 屏幕空间中，物体一般是在屏幕后面，那么物体的 \(z\) 值都是正的

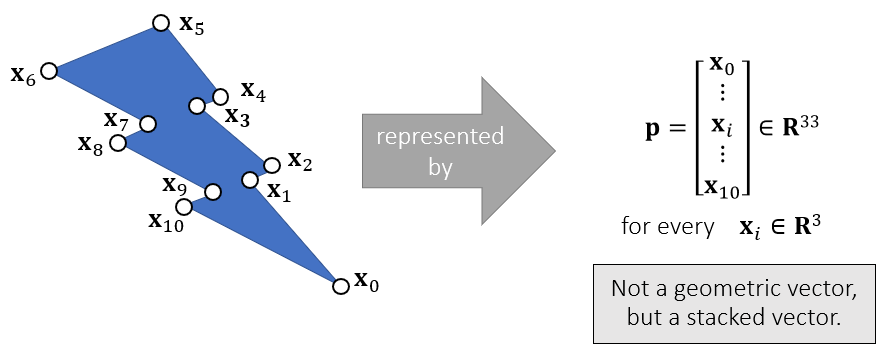
Stacked Vector

  • 矢量的定义（没有几何含义）
  • 可以只是由一堆数字组成，而不具备表示三维空间中的方向等几何含义
  • 常用于物体的描述
  • 例如用 11 个点表示一个闪电

矢量的运算

  • 矢量 \(\pm\) 矢量
  • 矢量的范数
    • 2-范数：长度
    • p-范数
    • 1-范数：曼哈顿距离
    • 无穷范数
  • 单位矢量：unit vector
    • 适量的单位化：normalization
  • 点乘
    • \(\mathbf{p}\cdot\mathbf{q}=0\)：向量垂直、正交

\[ \mathbf{p}\cdot\mathbf{q}=\langle\mathbf{p},\mathbf{q}\rangle=\mathbf{p}^{\mathbf{T}}\mathbf{q} \]

  • 叉乘
    • 右手系：\(\mathbf{p},\mathbf{q},\mathbf{r}\)
    • \(\Vert{r}\Vert=\Vert{p}\Vert\Vert{q}\Vert\sin\theta\)
    • \(\mathbf{p}\times\mathbf{q}=0\)：向量平行

\[ \mathbf{r}= \mathbf{p}\times\mathbf{q}= \begin{pmatrix} p_yq_z-p_zq_y\\ p_zq_x-p_xq_z\\ p_xq_y-p_yq_x\\ \end{pmatrix} \]

示例

(1) 表示基础量

  • Linear Representation
  • 矢量可以被用于描述如下的量
    • 位置、速度、力、直线、光线、线段
  • 匀速运动的粒子的位置

\[ \mathbf{p}(t)=\mathbf{p}+t\mathbf{v} \]

  • 直线，两个点 \(\mathbf{p},\mathbf{q}\)
    • 直线：\(t\in\mathbf{R}\)
    • 线段：\(0<t<1\)
    • 射线（光线）：\(t>0\)
  • 直线两种形式：运动形式、插值形式

\[ \mathbf{p}(t)=\mathbf{p}+t(\mathbf{q}-\mathbf{p}) \]

\[ \mathbf{p}(t)=(1-t)\mathbf{p}+t\mathbf{q} \]

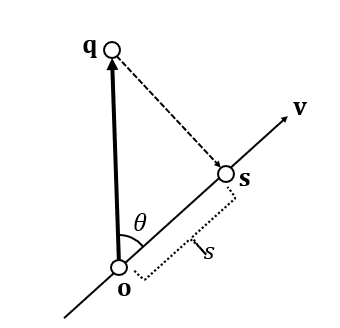
(2) 点到直线的投影

  • Paticle-Line Projection

\[ \begin{array}{c} s=(\mathbf{q}-\mathbf{o})^{\mathbf{T}}\dfrac{\mathbf{v}}{\Vert\mathbf{v}\Vert_2^2}=(\mathbf{q}-\mathbf{o})^{\mathbf{T}}\overline{\mathbf{v}}\\ \mathbf{s}=\mathbf{o}+s\overline{\mathbf{v}} \end{array} \]

(3) 平面的表示

  • Plane Representation

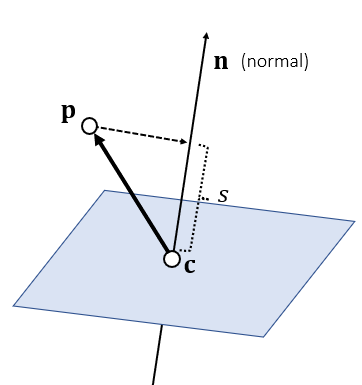\[ s=(\mathbf{p}-\mathbf{c})^{\mathbf{T}}\mathbf{n} \left\{ \begin{array}{rl} >0,&在平面上方\\ =0,&在平面内部\\ <0,&在平面下方\\ \end{array} \right. \]

  • 有向距离 \(s\)
    • 可以用于位置的判定
  • 如何判断一个点在多面体内部？
    • 在每个面的下方

(4) 粒子和球的碰撞

  • Particle-Sphere Collision

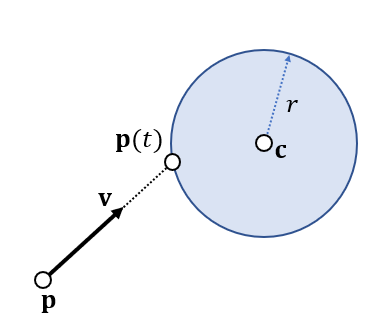
  • 判断如下式子是否有解

\[ \Vert\mathbf{p}(t)-\mathbf{c}\Vert=r^2 \]

  • 展开

\[ (\mathbf{v}\cdot\mathbf{v})t^2+2(\mathbf{p}-\mathbf{c})\cdot\mathbf{v}t+(\mathbf{p}-\mathbf{c})\cdot(\mathbf{p}-\mathbf{c})r^2=0 \]

  • \(t\ge0\) + 最近的点（最小的 \(t\)）

(5) 三角形面积和法向

  • Triangle Normal and Area

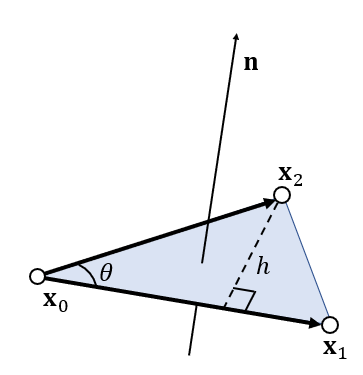
  • 记号

\[ \begin{array}{c} \mathbf{x}_{10}=\mathbf{x}_{1}-\mathbf{x}_{0}\\ \mathbf{x}_{20}=\mathbf{x}_{2}-\mathbf{x}_{0}\\ \end{array} \]

  • 法向（单位向量）

\[ \mathbf{n}=\dfrac{\mathbf{x}_{10}\times\mathbf{x}_{20}}{\Vert\mathbf{x}_{10}\times\mathbf{x}_{20}\Vert} \]

  • 面积

\[ S=\dfrac{\Vert\mathbf{x}_{10}\times\mathbf{x}_{20}\Vert}{2} \]

  • 定义三角形的时候，顶点顺序很重要
  • 如何判定三点共线？
    • 叉乘为 0

(6) 判定点是否在三角形内部

  • Triangle Inside/Outside Test

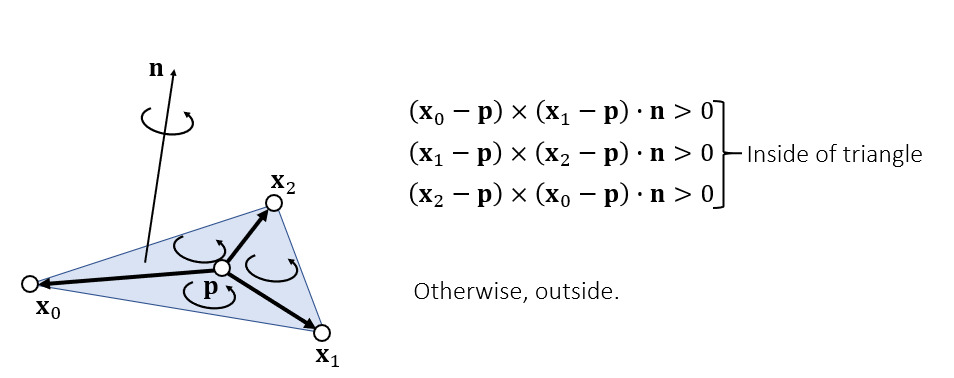
  • 或者直接 3 个叉乘符号值相同即可
    • 使用上面的判定方式能够更快排除掉点不在内部的情况

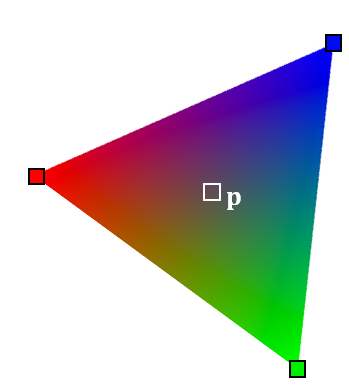
(7) 重心坐标系

  • Barycentric Coordinate

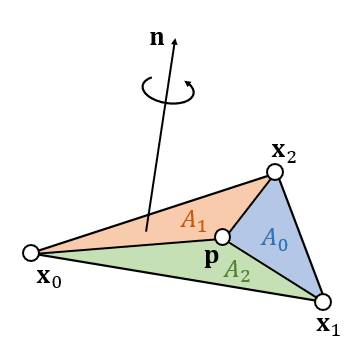
  • 表示面积大小

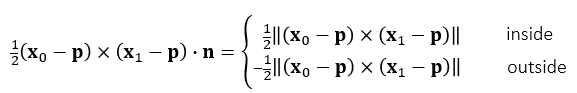
  • 有向面积大小

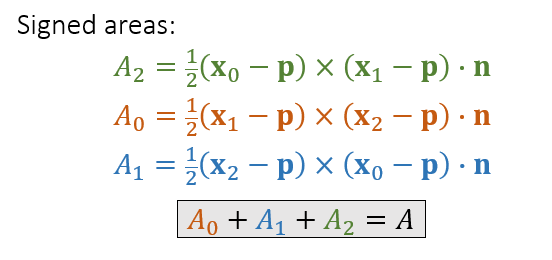
  • 重心坐标系

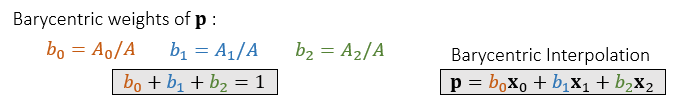
  • 使用重心坐标系对三角形内部的属性进行插值
    • Gouraud Shading
      • 早期硬件计算较弱的时候，使用这种方式减小 shading 的开销
        • 计算插值比 shading 计算快
      • 现在不流行了
    • 双线性插值，利用扫描线算法进行插值

(8) 四面体体积计算

  • Tetrahedral Volume

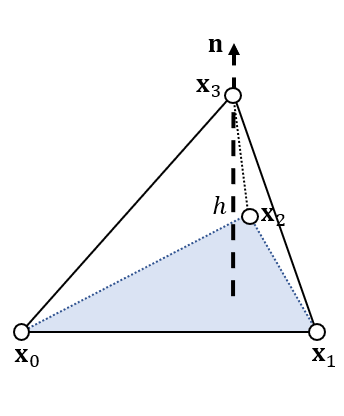
  • 边向量

\[ \begin{array}{c} \mathbf{x}_{10}=\mathbf{x}_{1}-\mathbf{x}_{0}\\ \mathbf{x}_{20}=\mathbf{x}_{2}-\mathbf{x}_{0}\\ \mathbf{x}_{30}=\mathbf{x}_{3}-\mathbf{x}_{0}\\ \end{array} \]

  • 体积

\[ \begin{aligned} V&=\dfrac{1}{3}Sh= \dfrac{1}{3} \left(\dfrac{1}{2}\Vert\mathbf{x}_{10}\times\mathbf{x}_{20}\Vert_2\right) \left(\mathbf{x}_{30}\cdot\mathbf{n}\right)\\ &=\dfrac{1}{3} \left(\dfrac{1}{2}\Vert\mathbf{x}_{10}\times\mathbf{x}_{20}\Vert_2\right) \left(\mathbf{x}_{30}\cdot\dfrac{\mathbf{x}_{10}\times\mathbf{x}_{20}}{\Vert\mathbf{x}_{10}\times\mathbf{x}_{20}\Vert_2}\right)\\ &=\dfrac{1}{6}\mathbf{x}_{30}\cdot(\mathbf{x}_{10}\times\mathbf{x}_{20}) \end{aligned} \]

  • 行列式表示方式：\(4\times4\)

\[ V=\left|\begin{array}{cccc} \mathbf{x}_1&\mathbf{x}_2&\mathbf{x}_3&\mathbf{x}_0\\ 1&1&1&1\\ \end{array}\right| \]

  • 体积是带正负的

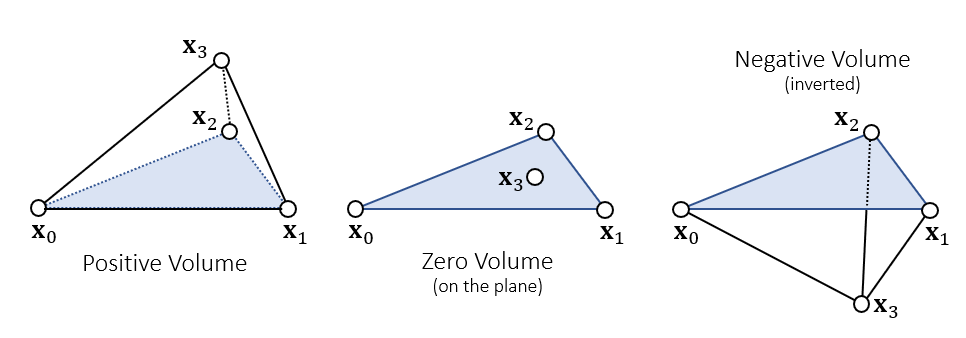
(9) 重心坐标系

  • Barycentric Weights
  • 中间的点将四面体划分为 4 个部分，4 个部分的体积占比对应对面的顶点的权重

(10) 移动粒子和三角形求交

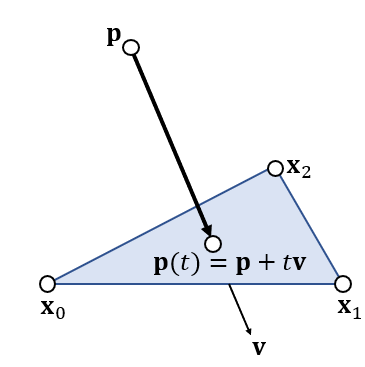
  • 首先求得时间 \(\mathbf{p}\) 和平面相交的时间 \(t\)

\[ (\mathbf{p}(t)-\mathbf{x}_0)\cdot(\mathbf{x}_{10}\times\mathbf{x}_{20})=0 \]

\[ t=-\dfrac {(\mathbf{p}-\mathbf{x}_0)\cdot(\mathbf{x}_{10}\times\mathbf{x}_{20})} {\mathbf{v}\cdot(\mathbf{x}_{10}\times\mathbf{x}_{20})} \]

  • 然后再判断 \(\mathbf{p}(t)\) 是否落在三角形内部

其他

  • 某论文
    • Vega: Nonlinear FEM Deformable Object Simulator