Ray Tracing The Next Week

Posted on Edited on In Views:
Ray Tracing The Next Week 学习

Ray Tracing The Next Week

  • 版本：3.2.3， 2020-12-07
  • 光追框架理解
  • 工程能力训练

1. 说明

2. 运动模糊

  • motion blur
  • 实际相机的快门开闭是有时间的，对这段时间内的光线做平均
  • 实现
    • 需要添加能够移动的物体
    • 相机需要有一个开闭时间
    • 光线上需要带一个时间戳，用于求交的时候确定物体的位置

效果图(100spp)

  • 大光圈

  • 大光圈 + 运动模糊

  • 小光圈 + 运动模糊

  • 小光圈

3. BVH

  • Bounding Volume Hierarchies
    • 包围盒（静态场景）
  • 之前光线和场景求交：逐个遍历所有物体
    • 加速方法
      • 拆分空间
      • 拆分物体：BVH
  • 基本思想：如果光线联保为何都没有击中，那么肯定不能击中物体
1
2
3
4
if (ray hits bounding object)
    return whether ray hits bounded objects;
else
    return false;
  • 包围盒例子

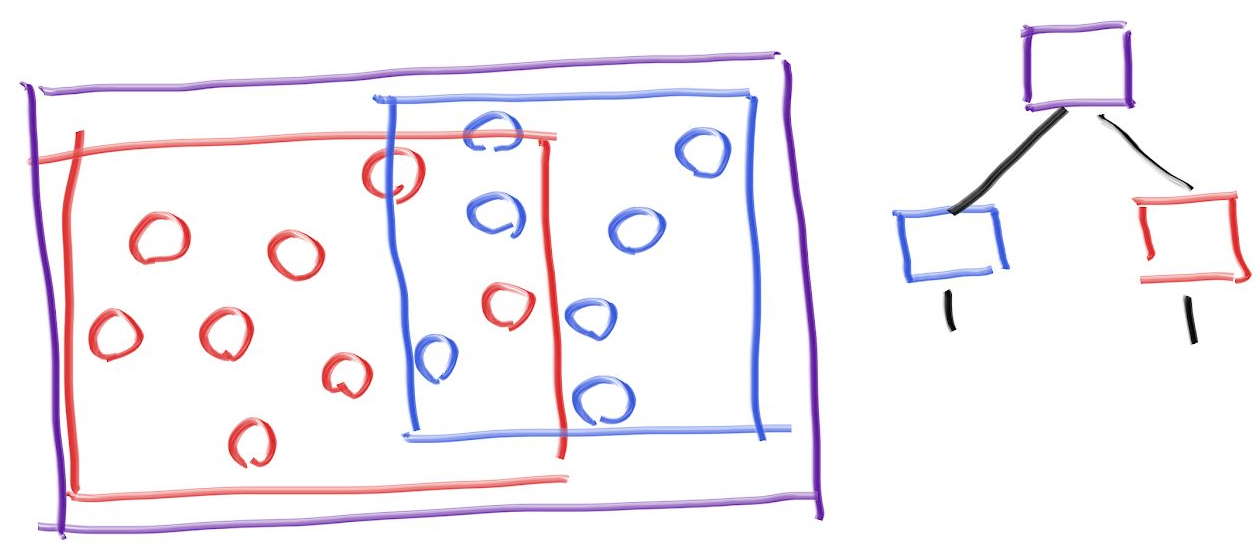
  • 因为有可能重合，击中左边的子结点之后，还有可能击中右边的子结点
1
2
3
4
5
6
7
if (hits purple) {
    hit0 = hits blue enclosed objects;
    hit1 = hits red enclosed objects;
    if (hit0 or hit1)
        return true and info of closer hit;
}
return false

AABB 包围盒

  • Axis-Aligned Bounding Boxes
    • 轴对齐的包围盒
  • 一个好的划分方式很重要
    • 中点划分
    • 等量划分
    • SAH

判断相交

  • 射线和平面求交

\[ \mathbf{P}(t) = \mathbf{A} + t \mathbf{b} \]

  • \(x\) 轴为例

\[ \begin{array}{c} x_0 = A_x + t_0 b_x\\ t_0 = \dfrac{x_0 - A_x}{b_x}\\ t_1 = \dfrac{x_1 - A_x}{b_x}\\ \end{array} \]

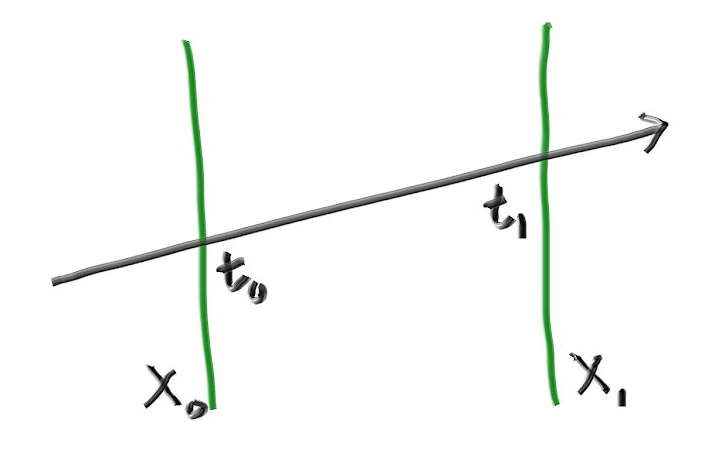
  • 三个维度的 \([t_0,t_1]\) 相交是否为空，不为空返回的就是光线和包围盒相交的部分
1
2
3
4
compute (tx0, tx1);
compute (ty0, ty1);
compute (tz0, tz1);
return overlap?( (tx0, tx1), (ty0, ty1), (tz0, tz1));

  • slab：就是指上面 \((x_0,x_1)\) 之间

  • 注意事项

    • \(t_1<t_0\)

      • 二者取大取小即可

    • 除 0

      • 浮点数可以自己处理这个情况

      1
      2
      3
      1.0/0.0 = inf;
      -1.0/0.0 = -inf;
      // inf > 1.0, 可以和一个实数值比大小

    • 光线起点在 slab 边界上而且恰好同时除 0

      • 0/0 的情况，造成 NaN

        • NaN 和任何数字相比都返回 false

        1
        2
        std::fmax(0.0 / 0.0, 1); // 1
        std::fmin(0.0 / 0.0, 1); // 1

      • 这种情况是恰好光线掠过边界，可以当作击中，也可以当作不击中

        • 我们认为不击中

建立包围盒

  • 在 hittable 物体中都加上一个包围盒函数
    • 返回值为 bool，不是所有的物体都包含包围盒（无限大的平面）
    • 对于移动的物体，我们直接返回这段时间内移动轨迹的包围盒

总结

  • 小场景中，包围盒加速效果不明显，甚至变慢
    • random 场景中，100ssp
      • 遍历：60s
      • BVH：120s

4. 纹理

  • Texture

球面纹理坐标

  • 经纬度
    • \(\phi\in[0,2\pi]\)
      • \(-x\to+z\to+x\to-z\)
    • \(\theta\in[0,\pi]\)
      • \(-y\to y\)
  • \([\theta,\pi]\to[u,v]\)
    • \(u,v\in[0,1]\)
    • \((u,v)=(0,0)\)：左下角

推导

\[ \begin{array}{rl} y=&-\cos{\theta}\\ x=&-\cos{\phi}\sin{\theta}\\ z=&\quad\sin{\phi}\sin{\theta}\\ \end{array} \]

\[ \begin{array}{c} \phi=\arctan\left(\dfrac{-x}{z}\right)\\ \theta=\arccos(-y)\\ \end{array} \]

1
2
phi = atan2(z, -x) + pi; // [-pi, pi] + pi
theta = acos(-y);

效果图

  • 高清大图：1000spp

5. 柏林噪声

  • Perlin Noise
  • 对于一个三维的输入产生一个实数输出
    • 同样的输入对应同样的输出
  • 简单、快速、有重复性
  • 柏林噪声参考
  • 非整数坐标点
    • 输入一个点 \(\to\) 根据周围的 8 个整数坐标点，三线性插值该点的噪声值
  • 整数坐标点
    • 每一个维度 （\(x,y,z\)）有一张排列表，根据排列表找到噪声值
    • 排列表可以直接保存噪声值（减少存储）
  • 效果图如下

  • 可以让噪声纹理更加高频

  • 柏林噪声插值的实际上是向量，每一个顶点都有一个随机向量
    • 将三线性插值的得到的向量点乘权重向量
    • 可能出现负值

  • Turbulence（湍流）
    • 将不同位置的柏林噪声以某种权重叠加在一起

  • 大理石样纹理
1
color(0.5 * (1 + sin(scale * p.z() + 10 * noise.turb(p))));

  • 加了个纹理小球（在反射中能够看到）

6. 图片纹理映射

  • 使用了 stb_image.h 库进行图片读取
  • 和之前没有什么不同，在材质读取 value 的时候，利用纹理坐标在图片上读取即可

7. 长方体和光源

(1) 光源

  • 光源的设置
    • 设置为一种材质，实现 material 类的 emitted 方法
      • 默认发白光
    • 光源不散射光线，因此 scatter 函数返回 false

(2) 长方形

  • 轴平齐的长方形
    • Axis Aligned
1
2
3
class xy_rect:public hitabble {}
class yz_rect:public hitabble {}
class zx_rect:public hitabble {}
  • cornell box 的例子

  • 1000spp 使用取余数的方法对比图

  • 不太清楚为什么上面会出现一条亮斑？
    • 麻了麻了，竟然是随机数的问题（100spp）
      • 下面直接取余数的方法，慢很多，大概时间花销在 4.5 倍左右
1
2
3
inline double random_double() {
    return rand() / (RAND_MAX + 1.0);
}

1
2
3
4
5
inline double random_double() {
    static std::uniform_real_distribution<double> distribution(0.0, 1.0);
    static std::mt19937 generator;
    return distribution(generator);
}

8. 实例化

(1) Box

  • box 很简单，就是直接画出 6 个面即可
  • 1000spp（mt19937）
    • 487 s

  • 1000spp（rand）
    • 1789 s

(2) 实例化

  • 一些对 box 的操作，平移旋转
    • 这里不支持矩阵的变换
  • 平移，旋转的设计
    • 包装，形成一个新的实例
  • 平移为例
1
2
3
4
5
class translate : public hittable {
    public:
        shared_ptr<hittable> ptr;
        vec3 offset;
};
  • 平移的的实现比较简单
    • 保存一个内部的物体、平移的量
    • 求交的时候可以先将光线的起点进行相同的平移，然后和内部物体进行判断求交
    • 如果有交点，那么修正交点即可（加上平移量）
      • 法线是不变的
  • 旋转则比较麻烦
    • 法线也会变化
    • 绕一个方向旋转的时候，法线变换和旋转变换相同
      • 正交矩阵：\((M^{-1})^{T}=M\)
    • 光线求交的时候先逆向旋转内部物体处（起点 + 方向）
    • 如果有交点，则对交点的位置和法向进行修正（初始的旋转，即正向的旋转）
  • 10000spp（rand）
    • 耗时 18480 s

9. 体积渲染

  • 参与介质
    • participating media
    • volume
  • 如果真的按照体渲染的方式进行渲染的话，需要对整个架构进行修改，和表面渲染大不相同
  • 一个实现的 trick
    • 用一个物体表示，但是它的表面以一定概率存在
    • 构造虚假的穿透效果

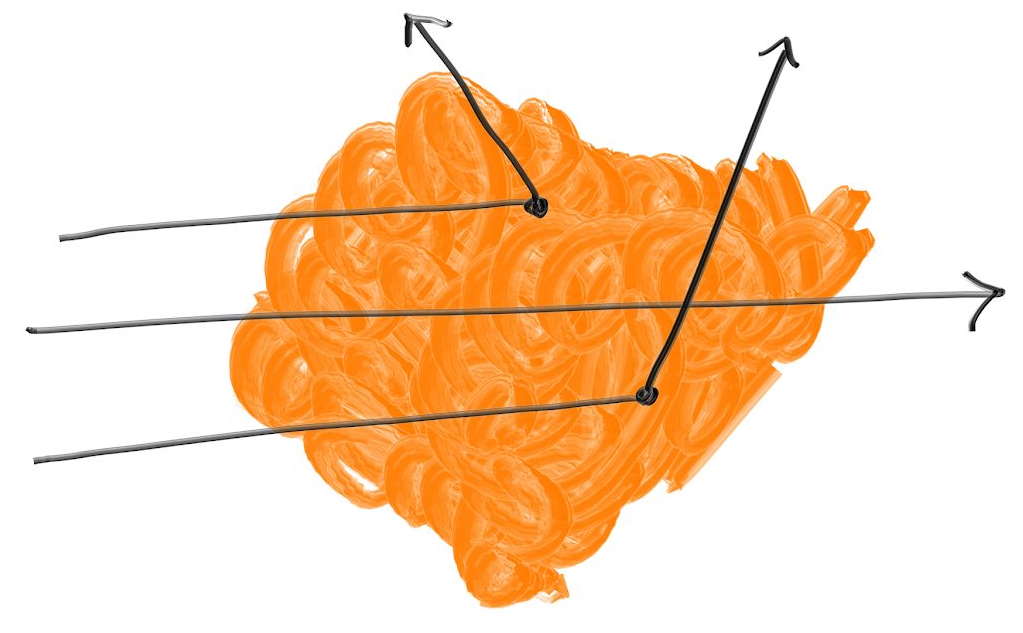
  • 光线可能直接穿过这个物体，可能在内部发生散射
  • 求出光线在内部的长度（在这段区域的任何部分都有可能被散射）
  • 假定密度为 1 的物体，散射距离为 \(\infty\)，那么在内部光线长度为 \(l\) 的散射概率如下
1
2
3
4
5
6
7
8
const auto distance_inside_boundary = (rec2.t - rec1.t) * ray_length;
// eps 为了防止 0 的出现, 理论是 0 是无穷似乎没问题
const auto hit_distance = neg_inv_density * log(random_double(1e-8, 1));
if (hit_distance > distance_inside_boundary) {
    // 不散射
    return false;
}
// 散射
  • 密度用于调整参与介质的大小，密度越大，可以散射的范围越小（分母越小），更容易散射

10. 最终场景

  • 1000spp
  • 400 x 400
  • 26287s = 7.30h

11. 随机数生成器的问题

  • 应该是 openmp 的理解问题，转换成单线程之后，mt19937 就没有亮带问题了

  • 学习一下 openmp

  • 随机数生成性能对比

    • 单线程来看二者是差不多的，甚至 rand 更快一些

    1
    2
    3
    10spp
    mt19937: 19s
    rand:    16s

  • 所以感觉是 openmp 没有处理 mt19937 的问题，造成了相关性，之后再看看具体内容

  • 27 核使用 mt19937 的并行结果快了 4 倍，但是使用 rand 和原来基本一样的速度

    • rand 在实现的时候加锁了，麻了，并行了，但是完全没有并行

  • 网上一篇文章也谈到这个问题

  • 确实是相关性问题导致的，改进随机数的生成方式

1
2
3
4
5
6
7
8
// 返回一个随机数 [0, 1)
inline double random_double() {
    static thread_local std::uniform_real_distribution<double> distribution(
        0.0, 1.0);
    static thread_local std::mt19937 generator(omp_get_thread_num());
    return distribution(generator);
    // return rand() / (RAND_MAX + 1.0);
}

  • 同时也发现了，inline 好像真的会有比较大的效率提升，大概是 2 倍
    • 把所有的函数都修改为不是 inline 之后，运行时间是原来的 2 倍左右
  • 如何真正的提高并行的效率呢？看了下别人写的代码，时间比能达到 16 倍（震撼）
  • 使用最终场景测试，发现好像不改之前的代码，openmp 也能有 15 倍的提升，看不懂了