计算方法B.裴玉茹.07.特征值与奇异值(2)

Posted on Edited on In Views:
特征值、相似矩阵、Schur 定理、Jacobi 方法、Gerschgorin 圆盘定理、求解单特征值（幂方法、逆幂方法）、收缩方法、Wielandt 收缩、Householder 变换、QR 分解（三对角线矩阵构造 QR）、平移方法
  • PPT（特征值）

特征值与奇异值

  • 特征值：Eigenvalue
  • 特征向量：Eigenvector

1. 定理

相似矩阵

  • 若存在非奇异矩阵 \(S\)，满足 \(A=S^{-1}BS\)，则称矩阵 \(A\) 与矩阵 \(B\) 为相似矩阵
  • 相似矩阵特征值相等
    • 假定 \(x\ne0\)
    • 那么有 \(S^{-1}BSx=Ax=\lambda x\)
    • \(BSx=SAx=\lambda Sx\)
    • 于是 \(\lambda\) 是矩阵 \(B\) 的特征值，\(Sx\) 是对应的特征向量

Schur 定理

  • \(A\) 为任意矩阵，存在非奇异矩阵 \(U\) 使得 \(T=U^{-1}AU\)，其中 \(T\) 为上三角矩阵，对角线元素为矩阵 \(A\) 的特征值

image-20211114185219902

  • 如果 \(A\) 是对称矩阵，则存在正交矩阵 \(Q\) 使得 \(D=Q^{-1}AQ=Q^{T}AQ\)，其中 \(D\) 为对角线矩阵，对角线元素为矩阵 \(A\) 的特征值

  • 如果 \(\Vert{Ux}\Vert_2=\Vert{x}\Vert_2\)，\(U\) 为酉矩阵，具有保范性质
    • 正交矩阵是酉矩阵

Jacobi 方法

  • 用于求解实对称矩阵的特征值
  • 通过旋转矩阵，构造相似矩阵
    • 如下是 \({\color{red}Q^{T}}\)

  • 旋转矩阵 \(Q\)：第 \(i,j\) 行出现和单位矩阵不一样的元素（\(\cos\theta,\sin\theta\)）
  • 记 \(B=Q^{-1}AQ\)，我们会发现 \(B\) 只有第 \(i,j\) 行和第 \(i,j\) 列和 \(A\) 不一样

\[ \left[\begin{matrix} b_{ii} & b_{ij} \\ b_{ji} & b_{jj} \\ \end{matrix}\right]=\left[\begin{matrix} c & -s \\ s& c \\ \end{matrix}\right]^T \left[\begin{matrix} a_{ii} & a_{ij} \\ a_{ji} & a_{jj} \\ \end{matrix}\right] \left[\begin{matrix} c & -s \\ s& c \\ \end{matrix}\right] \]

\[ \left[\begin{matrix} b_{ii} & 0 \\ 0 & b_{jj} \\ \end{matrix}\right]=\left[\begin{matrix} a_{ii}c^2+a_{jj}s^2+2csa_{ij} & cs(a_{jj}-a_{ii})+a_{ij}(c^2-s^2) \\ cs(a_{jj}-a_{ii}) + a_{ij}(c^2-s^2) & a_{jj}c^2+a_{ii}s^2-2csa_{ij} \end{matrix}\right] \]

  • 整个矩阵结果如下

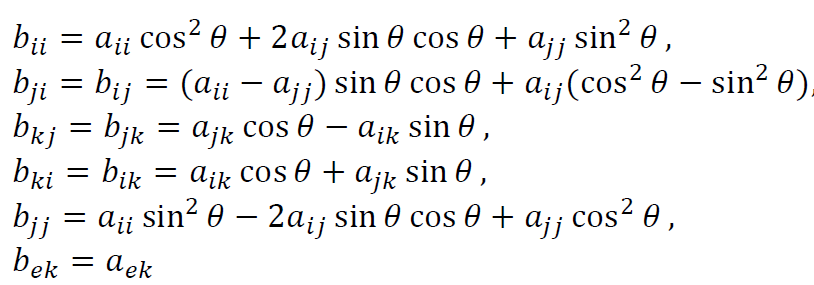
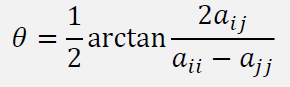
  • 思路：不断地消去非对角线元素
    • 正交变换 \(F\) 范数不变
    • 上述变换后，对角线上的元素平方和变大了，非对角线上元素的平方和变小了
    • 经过有限次变换，能够求得特征值

推论

  • 如果矩阵 \(A\) 为对称矩阵，其 \(n\) 个特征向量构成单位正交集，矩阵 \(A\) 的特征值为实数

正定性与特征值

  • 对称矩阵 \(A\) 为正定矩阵当且仅当矩阵 \(A\) 的所有特征值都是正数
    • 利用特征向量正交、线性即证
  • 证明

Gerschgorin 圆盘定理

  • \(k\) 个圆的并集指的是原本就相交形成的连通区域
  • 证明

2. 幂方法

  • note
  • 占优特征值
    • \(\lambda_1=\lambda_2=\cdots=\lambda_k\)
    • \(\lambda_1=-\lambda_2\)
      • 无法确定正负

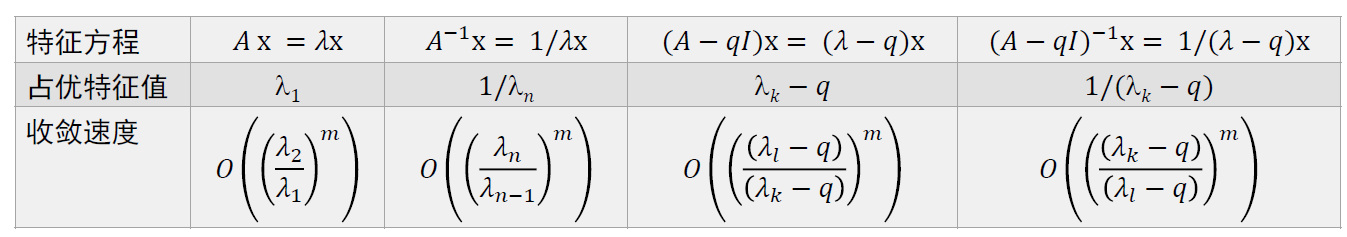
逆幂方法

  • \((A-qI)^{-1}x\) 使用幂方法
    • \(q\) 的选择决定了收敛速度
    • \(q\) 与特征值 \(\lambda_k\) 越接近，收敛越快

3. 收缩方法

  • 在计算了主特征值的近似值后，可以通过紧缩获得矩阵其它特征值

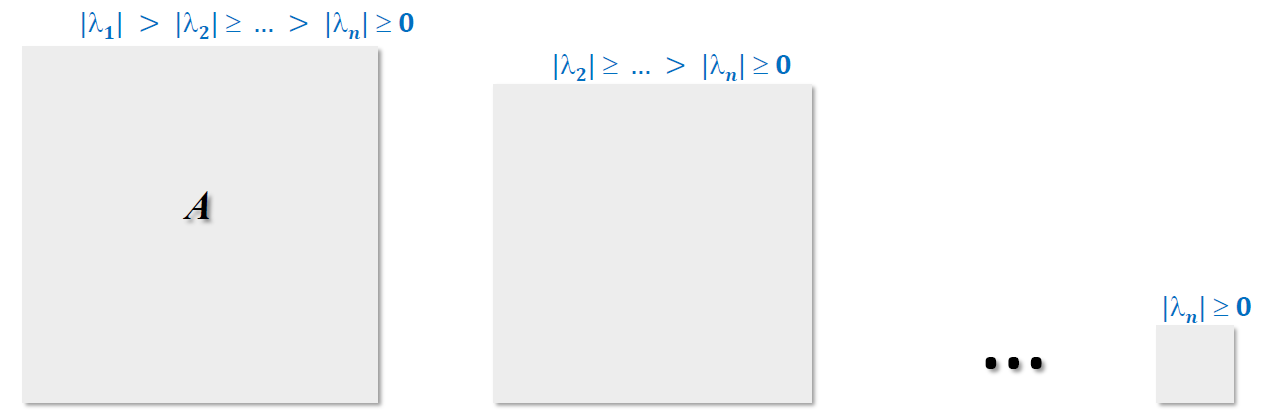
Wielandt 收缩

  • 构造一个新的矩阵 \(B\)，其特征值除了占优特征值之外与 \(A\) 相同，其中占优特征值被替换为 0
    • 只有占有特征值与 \(A\) 不同

定理

  • 假设 \(\lambda_1,\cdots,\lambda_n\) 是 \(A\) 的特征值，其特征向量 \(v^{(1)},\cdots,v^{(n)}\)，且 \(\lambda_1\) 的重数为 1
  • 设 \(x\) 为向量满足 \(x^{T}v^{(1)}=1\)，则矩阵 \(B=A-\lambda_1v^{(1)}x^{T}\)
    • \(B\) 的特征值为 \(0,\lambda_2,\cdots,\lambda_n\)，特征向量为 \(v^{(1)},w^{(1)}\cdots,w^{(n)}\)
    • \(v^{(i)}=(\lambda_i-\lambda_1)w^{(i)}+\lambda_1x^{T}w^{(i)}v^{(1)}\)

算法细节

  • 如何构造 \(x\)

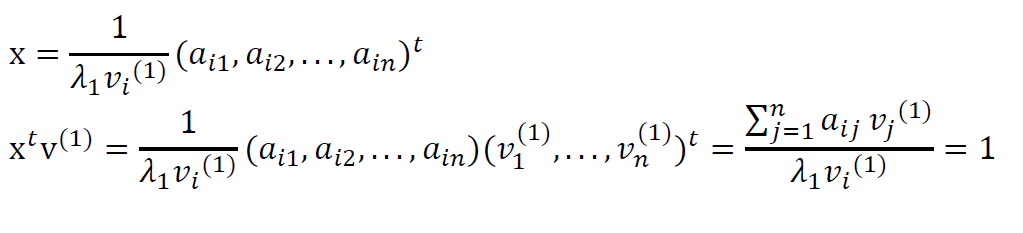
  • 发现矩阵 \(B=A-\lambda_1v^{(1)}x^{T}\) 的第 \(i\) 行全为 0
    • 代入即得
  • \(Bw=\lambda w\)
    • 因此，\(w\) 的第 \(i\) 个分量是 0，所以 \(B\) 的第 \(i\) 列对解没有贡献，去掉第 \(i\) 行和第 \(i\) 列得到 \((n-1)\times(n-1)\) 矩阵 \(B'\)
      • 行列式展开的角度也行
  • 对 \(B'\) 应用幂方法，得到 \(\lambda_2\) 与 \(w'^{(2)}\)， 并插入 0 得到 \(w^{(2)}\)
  • 问题：易受舍入误差影响

Householder 变换

  • \(P=I-2ww^{T}\)，其中 \(w^{T}w=1,w\in\mathbb{R}^{n}\)
    • \(P\) 是对称正交矩阵

目标

  • 利用 Householder 方法计算对称三对角线矩阵 \(B\)，其与给定的对称矩阵 \(A\) 相似

步骤

  • 定义矩阵变换 \(P^{(1)}\) 满足 \(A^{(2)}=P^{(1)}AP^{(1)}\)
    • 显然 \(P^{(2)}\) 是对称矩阵，\(P^{(1)},A\) 都是对称矩阵
  • 试图在变换后保证
    • \(a_{11}^{(2)}=a_{11}\)
      • \(w_1=0\) 即可
    • \(a_{j1}^{(2)}=0,(j=3,\cdots,n)\)
  • 也就是说，利用 HouseHolder 变换将 \((a_{21},a_{31},\cdots,a_{n1})^{T}\) 转换为 \((\alpha,0,\cdots,0)^{T}\)

  • \(\hat{w}^{T}\hat{y}\) 是 \(1\times1\) 的，因此可以提前
求解参数
  • 计算具体的 \(\alpha\) 值

\[ \begin{array}{c} (\alpha,0,\cdots,0)=(a_{21}-rw_2,a_{31}-rw_3,\cdots,a_{n1}-rw_n)\\ 其中\ r=\hat{w}^{T}\hat{y}\\ \end{array} \]

\[ \begin{array}{c} \alpha=a_{21}-rw_2\\ a_{i1}-rw_i=0,i=3,\cdots,n\\ \end{array} \]

  • 对 \(2rw_i\) 平方求和

\[ 4r^2\sum_{j=2}^{n}w_j^2=(a_{21}-\alpha)^{2}+\sum_{j=3}^{n}a_{j1}^{2} \]

  • 左边：\(4r^{2}(1-w_{1}^{2})=4r^{2}\)

\[ 4r^{2}=-2\alpha a_{21}+\alpha^{2}+\sum_{j=2}^{n}a_{j1}^{2} \]

  • 再由 \(P\) 的正交性

\[ \alpha^{2}=(\hat{P}\hat{y})^{T}(\hat{P}\hat{y})=\hat{y}^{T}\hat{P}^{T}\hat{P}\hat{y}=\hat{y}^{T}\hat{y}=\sum_{j=2}^{n}a_{j1}^{2} \]

  • 结合上面两个式子，得到

\[ 2r^{2}=-\alpha a_{21}+\sum_{j=2}^{n}a_{j1}^{2}=-\alpha a_{21}+\alpha^{2} \]

  • 可以求解得到 \(\alpha,w\)

\[ \alpha=-\mathrm{sgn}(a_{21})\sqrt{\sum_{j=2}^{n}a_{j1}^{2}} \]

\[ 2r^{2}=-\alpha a_{21}+\alpha^{2} \]

\[ \begin{array}{c} w_2=\dfrac{a_{21}-\alpha}{2r}\\ w_i=\dfrac{a_{i1}}{2r},i=3,\cdots,n \end{array} \]

  • 之后的步骤类似前面的，收缩方法

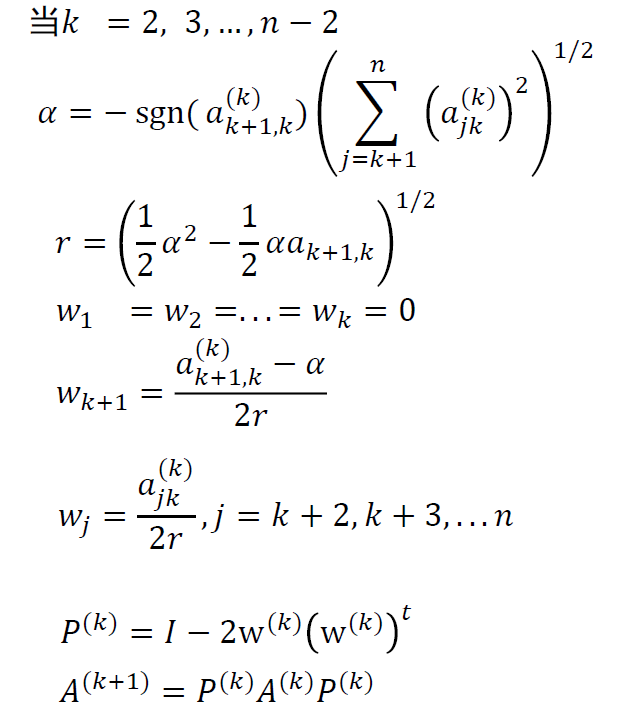
4. QR 迭代

  • QR 方法
    • 同时确定对称矩阵所有特征值的矩阵约化方法
    • QR 方法可以生成一组矩阵 \(A=A^{(1)},A^{(2)},\cdots,A^{(n)}\)
    • \(A^{(1)}=A\) 分解为矩阵乘积 \(A^{(1)}=Q^{(1)}R^{(1)}\)
      • \(Q^{(1)}\) 为正交矩阵
      • \(R^{(1)}\) 为上三角矩阵
    • \(A^{(2)}\) 定义为 \(A^{(2)}=R^{(1)}Q^{(1)}\)
    • 接着继续对 \(A^{(2)}\) 进行 QR 分解
    • 可以得到 \(A^{(i+1)}=(Q^{(i)})^{T}A^{(i)}Q^{(i)}\)
      • 相似变换，特征值不变
  • \(A^{(i+1)}\) 与 \(A^{(i)}\) 具有相同的特征值，\(A^{(i+1)}\) 变为对角线矩阵，其对角线上值为矩阵 \(A\) 的特征值

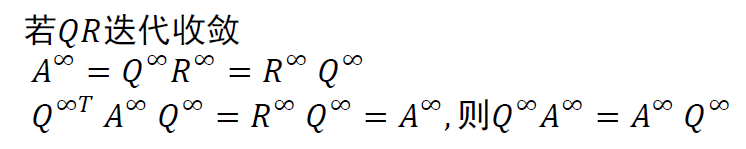
  • \(Q^{\infty}\) 与 \(A^{\infty}\) 的特征向量相同
    • \(AB=BA\) \(\Rightarrow\) \(A\) 与 \(B\) 具有相同的特征向量
  • 由于 \(Q^{\infty}\) 是正交矩阵，\(Q^{\infty}\) 的特征值为 \(\pm1\)
  • 假设 \(A^{\infty}x=\lambda x\)，则有

\[ \lambda x=A^{\infty}x=Q^{\infty}R^{\infty}x=R^{\infty}Q^{\infty}x=\pm R^{\infty}x \]

  • 得出结论
    • \(A^{\infty}\) 的特征值与 \(A\) 的特征值相同
    • 与 \(R^{\infty}\) 的特征值相同，即 \(R^{\infty}\) 的对角线元素（可能会差符号）
    • 与 \(Q^{\infty}\) 的特征向量相同

构造 QR

  • 考虑旋转矩阵
    • 旋转矩阵为正交矩阵
      • \(p_{ii}=p_{jj}=\cos\theta,p_{ji}=-p_{ij}=\sin\theta\)

三对角线稀疏矩阵

  • 矩阵 \(A\) 为三对角线矩阵 ，对其使用旋转矩阵进行 QR 分解
    • 让对角线以下元素变成 0
    • (1,3) 可能变为非零向量，(1,4)、(1,n) 为 0

  • 算法流程

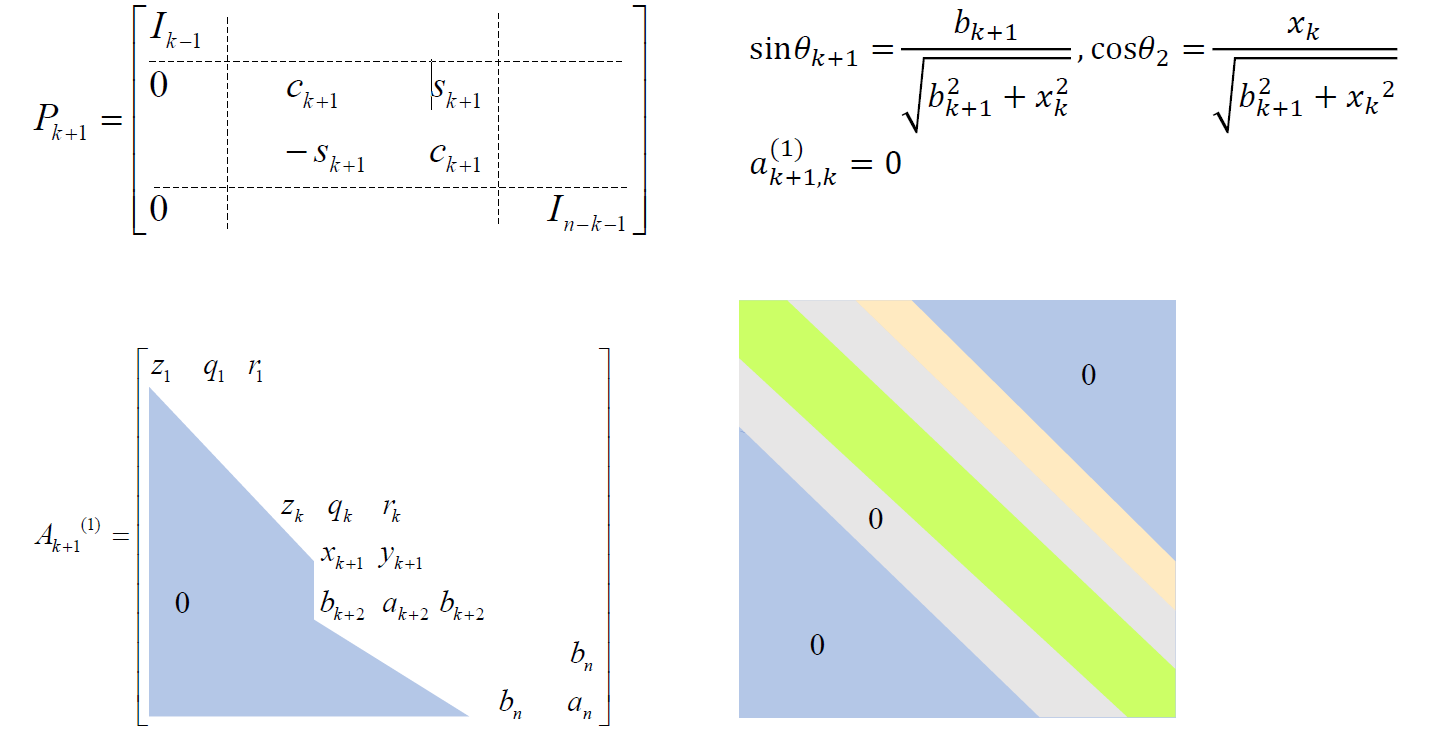
  • 矩阵 \(A\) 三对角线最上面一条对角线不一定需要和最下面相同，不需要为 \(b_n\)
  • 接着使用上面的方法进行迭代
  • \(A^{(2)}\) 对角线以外的项比 \(A^{(1)}\) 的相应项小，\(A^{(1)}\) 更接近对角矩阵
  • 为什么 \(A^{(2)}\) 还是三对角线矩阵 ？
    • \(A^{(2)}=(Q^{(1)})^{T}A^{(1)}Q^{(1)}\)
    • 因为旋转矩阵只会影响行列 \(i,j\)
    • note
  • 收敛速度
    • 对于特征值\(\vert\lambda_1\vert>\vert\lambda_2\vert>\cdots>\vert\lambda_n\vert\)
    • \(A^{(i+1)}\) 的元素 \(b_{j+1}^{(i+1)}\) 收敛到 0 的速度依赖于比值 \(\dfrac{\vert{\lambda_{j+1}}\vert}{\vert{\lambda_{j}}\vert}\)，接近于 1 的时候收敛速度较慢

平移方法（三对角线）

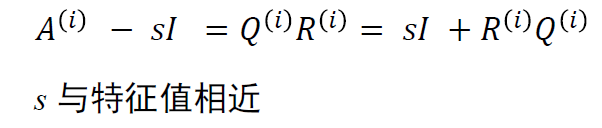
  • 当 \(b_n^{(i+1)}\) 足够小，假设 \(\lambda_n\approx a_n^{(i+1)}\)
  • 删除矩阵的第 n 行与第 n 列，计算 \(\lambda_{n-1}\)
  • 收敛速度依赖于 \(\dfrac{\vert{\lambda_{j+1}-s}\vert}{\vert{\lambda_{j}-s}\vert}\) , 一般为三阶收敛速度 平移需要加回到特征值