计算方法B.裴玉茹.07.特征值与奇异值
- 数值分析课本第 12 章(特征值与奇异值) + PPT(特征值)
特征值与奇异值
- 求解矩阵 \(A\) 的特征值
\[ \det(\lambda I-A)=0 \]
1. 幂迭代方法
- 一次求出一个特征值
1.1 幂迭代
- 幂迭代的动机:与矩阵相乘可以将向量推向主特征向量的方向
占优特征值
- 令 \(A\) 是一个 \(m\times m\) 矩阵,\(A\)
的占优特征值是量级比矩阵 \(A\) 所有其他特征值都大的特征值 \(\lambda\)
- 如果这样的特征值存在,与 \(\lambda\) 相关的特征向量被称为占优特征向量
- 绝对值最大的特征值
- 对于任意的初始向量,\(A^{n}x\) 会趋近于占优特征向量
- \(x\) 可以由特征向量线性表出
- \(A^{n}x\) 会被占优特征向量占优
- 计算过程中,每一步都进行归一化,可以不让数字失去控制
- 这不影响占优,对所有向量都是一个等比例的操作
瑞利商
- Rayleigh
- 最小二乘
- 特征值方程:\(x\lambda=Ax\)
- 其中,\(x\) 是特征向量的近似
- 法线方程:\(x^{T}x\lambda=x^{T}Ax\Rightarrow\lambda=\dfrac{x^{T}Ax}{x^{T}x}\)
- \(Ax=b\Rightarrow A^{T}Ax=A^{T}b\)
- 特征值方程:\(x\lambda=Ax\)
- 瑞利商是在最小二乘意义下的最优特征值近似
幂迭代算法
\[ \begin{array}{l} 给定初始向量\ x_0\\ \begin{array}{rl} \mathrm{for}&j=1,2,3,\cdots\\ &u_{j-1}=\dfrac{x_{j-1}}{\Vert{x_{j-1}}\Vert_2}\\ &x_j=Au_{j-1}\\ &\lambda_j=u_{j-1}^{T}Au_{j-1}=u_{j-1}^{T}x_{j}\\ \mathrm{end}\\ \end{array}\\ u_{j}=\dfrac{x_{j}}{\Vert{x_{j}}\Vert_2}\\ \end{array} \]
1.2 幂迭代的收敛

- 线性收敛
- 收敛常数 \(\left\vert\dfrac{\lambda_2}{\lambda_1}\right\vert\)
证明
- 线性表出

1.3 幂迭代的逆
- 幂迭代算法可以用于求解绝对值最大的特征值
- 虽然可以通过每次减去最大特征值对应特征向量,来实现求解次大特征值,从而求解所有特征值
- 但是由于累计误差的存在,之后求解得到的特征值不可靠
- 幂迭代用于矩阵的逆矩阵,则可以求解绝对值最小的特征值
引理

- 证明
\[ \begin{array}{rl} Av_1=\lambda_1v_1&\Rightarrow v_1=A^{-1}\lambda_1v_1\\ &\Rightarrow A^{-1}v_1=\lambda_1^{-1}v_1\\ Av_1=\lambda_1v_1&\Rightarrow (A-sI)v_1=Av_1-sv_1=(\lambda_1-s)v_1&\\ \end{array} \]
- 求逆等价于高斯消去
\[ x_{k+1}=A^{-1}x_k\Longleftrightarrow Ax_{k+1}=x_k \]
- 加上转移矩阵,如果我们知道特征值的近似,可以求出这个特征值
- 离这个特征值最近(最小)
逆向幂迭代算法
\[ \begin{array}{l} 给定初始向量\ x_0,平移\ s\\ \begin{array}{rl} \mathrm{for}&j=1,2,3,\cdots\\ &u_{j-1}=\dfrac{x_{j-1}}{\Vert{x_{j-1}}\Vert_2}\\ &求解\ (A-sI)x_j=u_{j-1}\\ &\lambda_j=u_{j-1}^{T}(A-sI)^{-1}u_{j-1}=u_{j-1}^{T}x_{j}\\ \mathrm{end}\\ \end{array}\\ u_{j}=\dfrac{x_{j}}{\Vert{x_{j}}\Vert_2}\\ \end{array} \]
1.4 瑞利商迭代(RQI)
- 在逆向幂迭代算法中,同时更新近似的特征值 \(s\to \lambda_{j-1}\)
瑞利商算法
- 求得的特征值就是原始矩阵 \(A\)
的占优特征值
- 依赖于:逆矩阵、转移矩阵的特征向量和原始矩阵相同
\[ \begin{array}{l} 给定初始向量\ x_0\\ \begin{array}{rl} \mathrm{for}&j=1,2,3,\cdots\\ &u_{j-1}=\dfrac{x_{j-1}}{\Vert{x_{j-1}}\Vert_2}\\ &\lambda_j=u_{j-1}^{T}Au_{j-1}\\ &求解\ (A-\lambda_{j}I)x_j=u_{j-1}\\ \mathrm{end}\\ \end{array}\\ u_{j}=\dfrac{x_{j}}{\Vert{x_{j}}\Vert_2}\\ \end{array} \]
1.5 总结
- 收敛速度
- 逆向幂迭代线性收敛
- 瑞利商迭代则二次收敛到单特征值(非重复),如果矩阵对称则可以得到三次收敛
- 收敛后矩阵 \(A-\lambda_{j-1}I\)
为奇异矩阵,不能继续迭代
- 因而可以通过误差测试使得在这种情况出现之前终止迭代(提前结束)
- RQI 复杂度提高了
- \(Ax=b\) 中如果 \(A\) 不改变,则只需要一次 LU 分解,参考 note
- 逆向幂迭代仅仅需要一次 LU 分解
- 但是对于 RQI,每步还需要一次分解,这是由于平移量的改变
- \(Ax=b\) 中如果 \(A\) 不改变,则只需要一次 LU 分解,参考 note
2. QR 方法
- 一次求出所有特征值
2.1 同时迭代
- 对称矩阵
- 对称矩阵的特征值为实数,其特征向量构成 \(\mathbb{R}^{m}\) 空间的一组单位正交基
- 思路:初始给定一组正交基,同时幂迭代,得到最终的特征向量
- 但是幂迭代会让任意向量趋向占优特征向量
- 每次迭代结束对其正交化
- 假设 \(\lambda_1\) 准确找到,那么 \(Av_2\) 向量最终会趋向于次优特征向量(因为没有占优特征向量的成分)
一个例子
- 初始正交基为初等基向量
- QR 分解
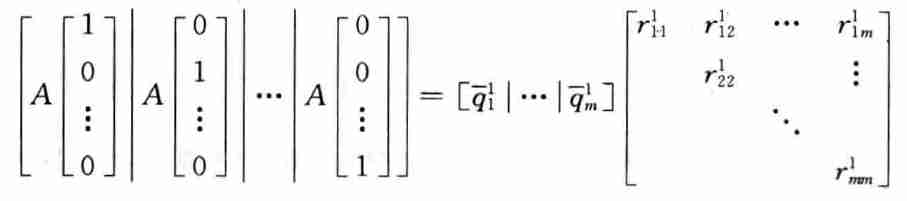
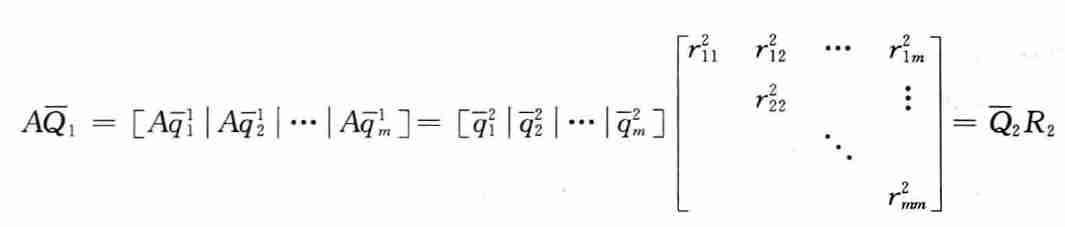
算法
\[ \begin{array}{rll} 设& \overline{Q}_0=I&\\ \mathrm{for}&j=1,2,3,\cdots&\\ &A\overline{Q}_j=\overline{Q}_{j+1}R_{j+1}&(QR分解)\\ \mathrm{end}&&\\ \end{array}\\ \]
- 在第 \(j\) 步中,\(\overline{Q}_j\) 的列就是 \(A\) 的特征向量的近似,对角线元素 \(r_{ii}\) 是近似的特征值
无移动的 QR 算法
- 原始迭代:\(\overline{Q}_0=I\)
- 12.7
\[ \begin{array}{c} A\overline{Q}_0=\overline{Q}_1R_1\\ A\overline{Q}_1=\overline{Q}_2R_2\\ A\overline{Q}_2=\overline{Q}_3R_3\\ \cdots\ \end{array} \]
- 相似的迭代:\(Q_0=I\)(无移动的 QR
算法)
- 12.8
\[ \begin{array}{c} A_0\equiv AQ_0=Q_1R_1'\\ A_1\equiv R_1'Q_1=Q_2R_2'\\ A_2\equiv R_2'Q_2=Q_3R_3'\\ \cdots\ \end{array} \]
- 区别:用 \({\color{red}R_i'}Q_i\) 代替 \({\color{red}A}Q_i\)

- 因此输出的特征向量矩阵为 \(\overline{Q}_j=Q_1\cdots Q_{j-1}\)
- 定理

- 对称条件
2.2 实数舒尔形式和 QR 算法
- QR 算法找到矩阵 A
的特征值的方式是寻找相似矩阵,该相似矩阵对应的特征值更明显
- 相似矩阵具有相同的特征值,但是不一定有相同的特征向量
- 一个例子是实数舒尔形式
实数舒尔形式
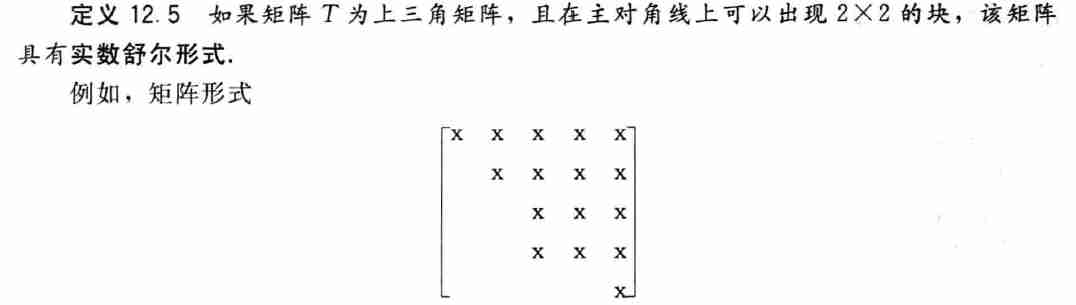
定理
- 令 \(A\) 是实数元素的方阵,则存在正交矩阵 \(Q\) 以及实数舒尔形式的矩阵 \(T\),满足 \(A=Q^TTQ\)
平移版本
- 一步迭代:先平移,完成 QR 分解之后平移回来
\[ \begin{array}{rl} A_0-sI&=Q_1R_1\\ A_1&=R_1Q_1+sI\\ \end{array} \]
- 注意到
\[ A_1-sI=R_1Q_1=Q_1^{T}(A_0-sI)Q_1=Q_1^{T}A_0Q_1-sI \]
- 于是重复上述步骤,我们能够得到一系列和 \(A_0\) 相似的矩阵 \(A_k\)
- 最优的平移

- 算法如下

- 该算法基于上面的定理,如下情况会出问题
- 复数特征值
- 相同量级的实数特征值
复数特征值
- 为了计算复数特征值,我们需要允许对角线上有 \(2\times 2\) 的块
- 如果在指定次数的迭代后无法得到特征值,则收缩 \(2\times 2\)

- 对于重复的复数特征值,无法解决,例如
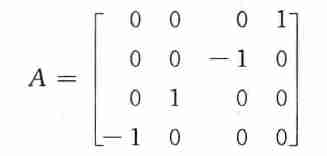
2.3 上海森伯格形式
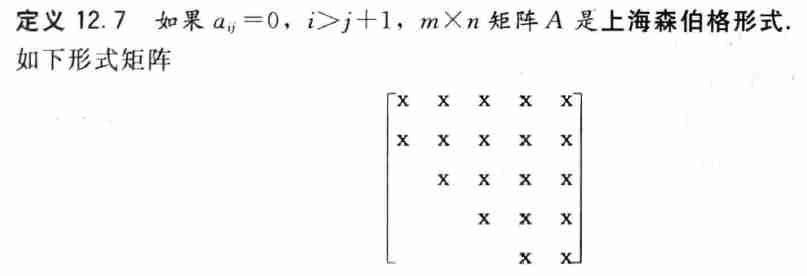
- 如果首先将 \(A\) 变换为上海森伯格形式,QR 算法的效率可以大大提高
- 这种思想是在 QR 迭代之前应用相似变换,在 \(A\) 中放置尽可能多的 0,而同时保持特征值
- 此外,上海森伯格形式将消去我们已经推导的 QR 算法形式中最后的难点,可以收敛到重复的复数特征值,这是通过保证 QR 迭代总能收敛到 \(1\times1\) 或者 \(2\times2\) 的块
定理
- 令 \(A\) 是实数元素的方阵,则存在正交矩阵 \(Q\) 以及上海森伯格形式的矩阵 \(B\),满足 \(A=Q^TBQ\)
- 豪斯霍尔德反射子
算法

- MATLAB 算法
- \(H=I-2P\):查看之前的笔记

- 上海森伯格形式对于特征值计算的优势
- 仅有 \(2\times2\) 的块可以出现在 QR 算法中的对角线上
- 这避免了前面章节中重复的复数特征值所带来的计算困难
2.4 总结
- 利用相似矩阵有相同的特征值,构造特征值更明显的相似矩阵
- 问题
- 没太懂上海森伯格形式为啥解决了重复复数特征值的问题
- 怎么解决重复的实数特征值问题的