Ray Tracing in One Weekend

Posted on Edited on In Views:
Ray Tracing in One Weekend 学习

Ray Tracing in One Weekend

  • 版本：3.2.3， 2020-12-07
  • 光追框架理解
  • 工程能力训练

1. ppm 文件格式

1
2
3
4
5
6
7
8
9
10
11
12
# 文件头
P3           # "P3" 表示这是一张 RGB 颜色空间的图片, 使用 ASCII 编码
3 2          # 图片大小为 3*2
255          # 255 表示最大的颜色编码

# 文件数据
255   0   0  # red
  0 255   0  # green
  0   0 255  # blue
255 255   0  # yellow
255 255 255  # white
  0   0   0  # black
  • 上面例子的图片如下

img

  • windows 可以使用工具 xnview 查看
    • xnview 好像不支持 P3 格式，支持 P6 格式
  • P3 和 P6 格式的唯一区别就是 P3 使用 ASCII 码存储，而 P6 使用二进制存储
  • 图像头文件库：stb_image.h

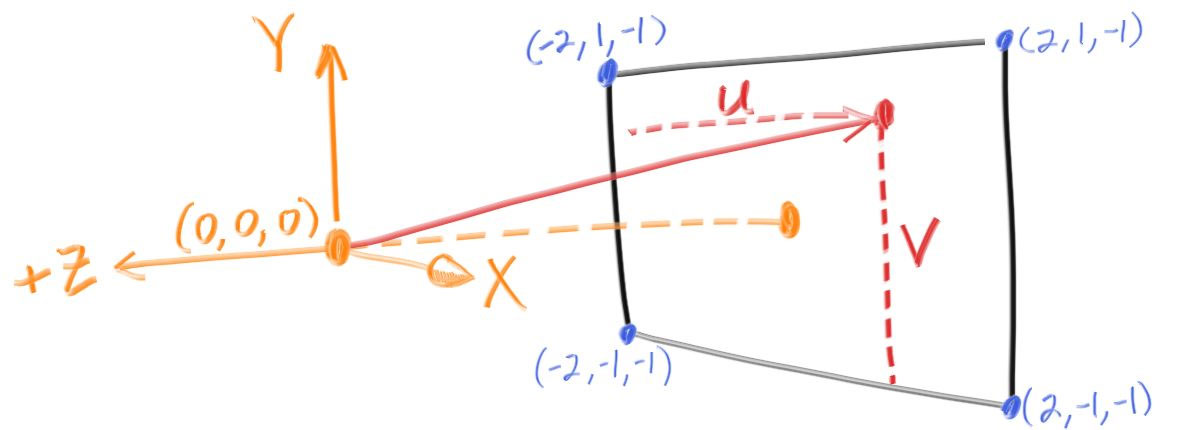
2. 坐标系说明

  • 视点：\((0,0,0)\)
  • 视窗
    • 高度设置为 \(2\)，宽度由 aspect ratio 计算得到（一般使用 16:9）
    • \(z=-1\)：focal length

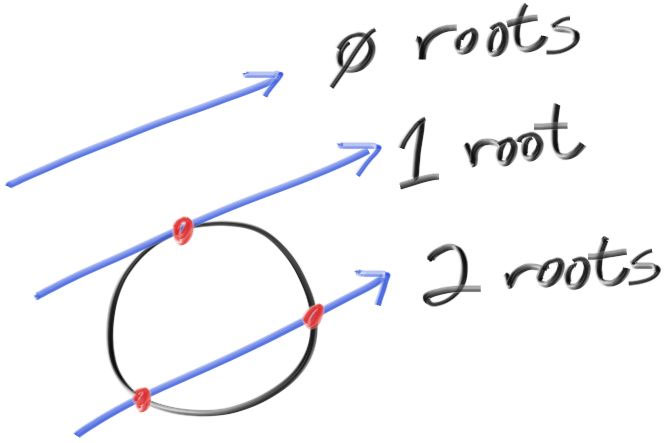
3. 光线与球求交

\[ \begin{array}{c} (\mathbf{P}(t) - \mathbf{C}) \cdot (\mathbf{P}(t) - \mathbf{C}) = r^2\\ (\mathbf{A} + t \mathbf{b} - \mathbf{C}) \cdot (\mathbf{A} + t \mathbf{b} - \mathbf{C}) = r^2\\ t^2 \mathbf{b} \cdot \mathbf{b} + 2t \mathbf{b} \cdot (\mathbf{A}-\mathbf{C}) + (\mathbf{A}-\mathbf{C}) \cdot (\mathbf{A}-\mathbf{C}) - r^2 = 0\\ \end{array} \]

  • 简化，令 \(b=2h\)

\[ \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}== \frac{-h \pm \sqrt{h^2 - ac}}{a} \]

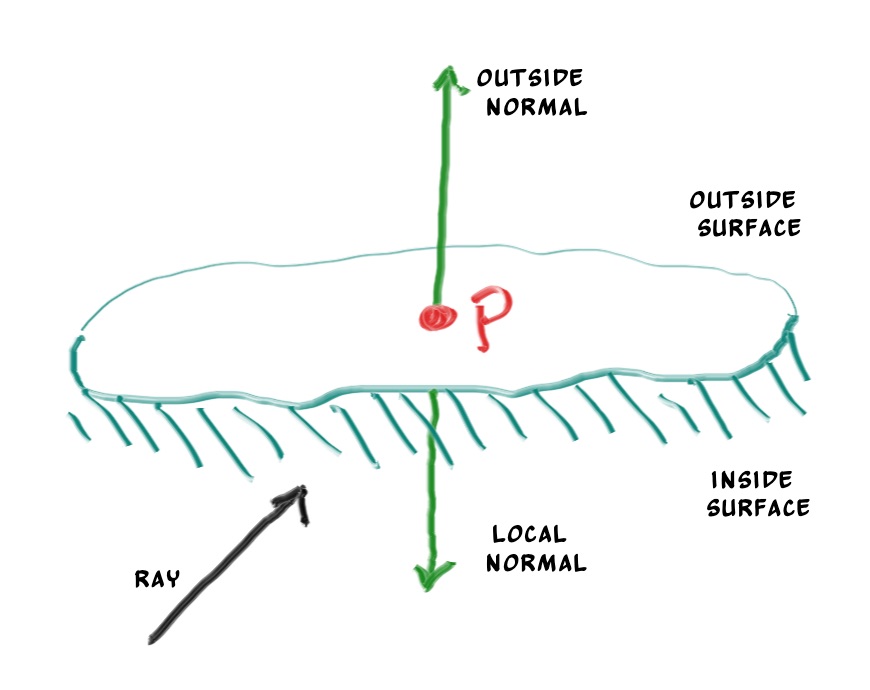
  • 判断光线是从圆内部射出还是外部射入
1
2
3
4
5
6
7
8
9
10
bool front_face;
if (dot(ray_direction, outward_normal) > 0.0) {
    // ray is inside the sphere
    normal = -outward_normal; // 此时法线反向
    front_face = false;
} else {
    // ray is outside the sphere
    normal = outward_normal;
    front_face = true;
}

4. 抗锯齿

  • 对每一个像素产生多条光线

5. 漫反射材质

  • diffuse

  • 随机出射
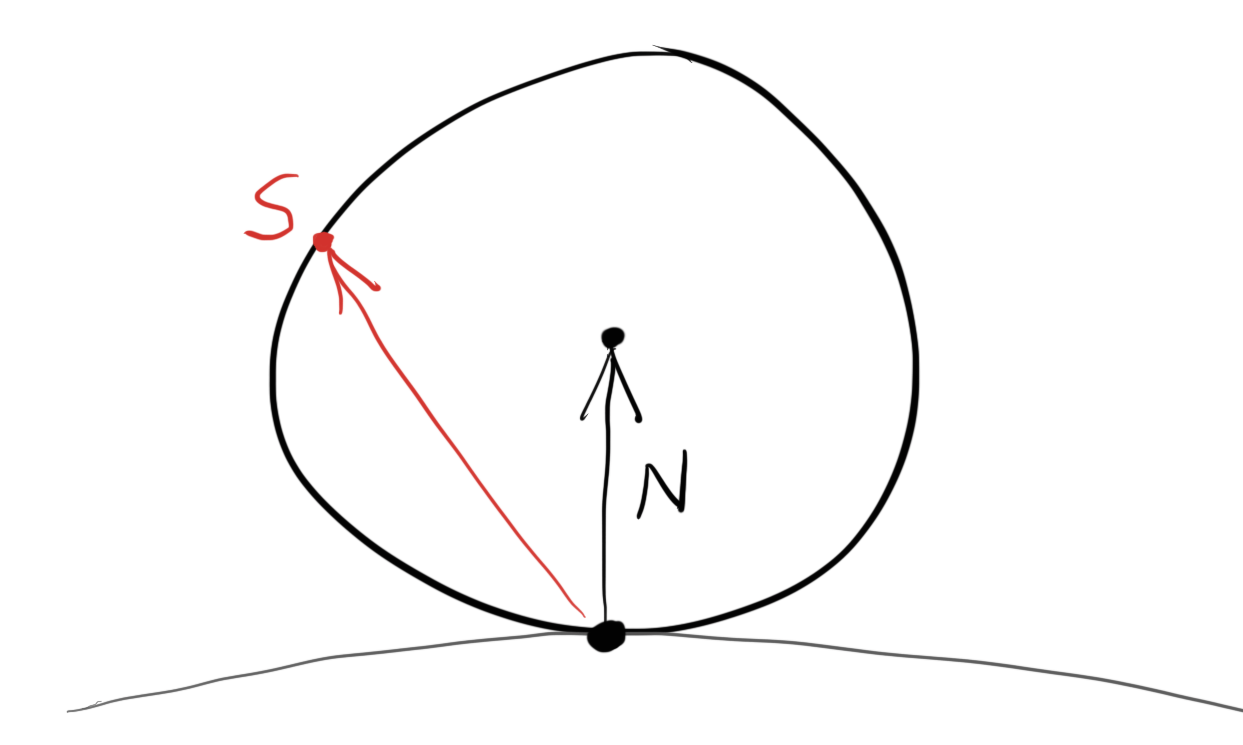
    • 在球体内部随机采样：在一个正方体中采样，判断长度是否落在球体内部

  • 上述采样方法，假设出射光线和法线的夹角为 \(\phi\)，那么概率分布密度函数系数为 \(\cos^{3}{\phi}\)
    • 算出来是 \(\cos^{3}{\phi}\sin{\phi}\)
      • 注意是 3D 的
    • 因为入射光线和法线的夹角大多较大，因此整体结果偏黑
  • 朗伯反射的系数应该是 \(\cos{\phi}\)
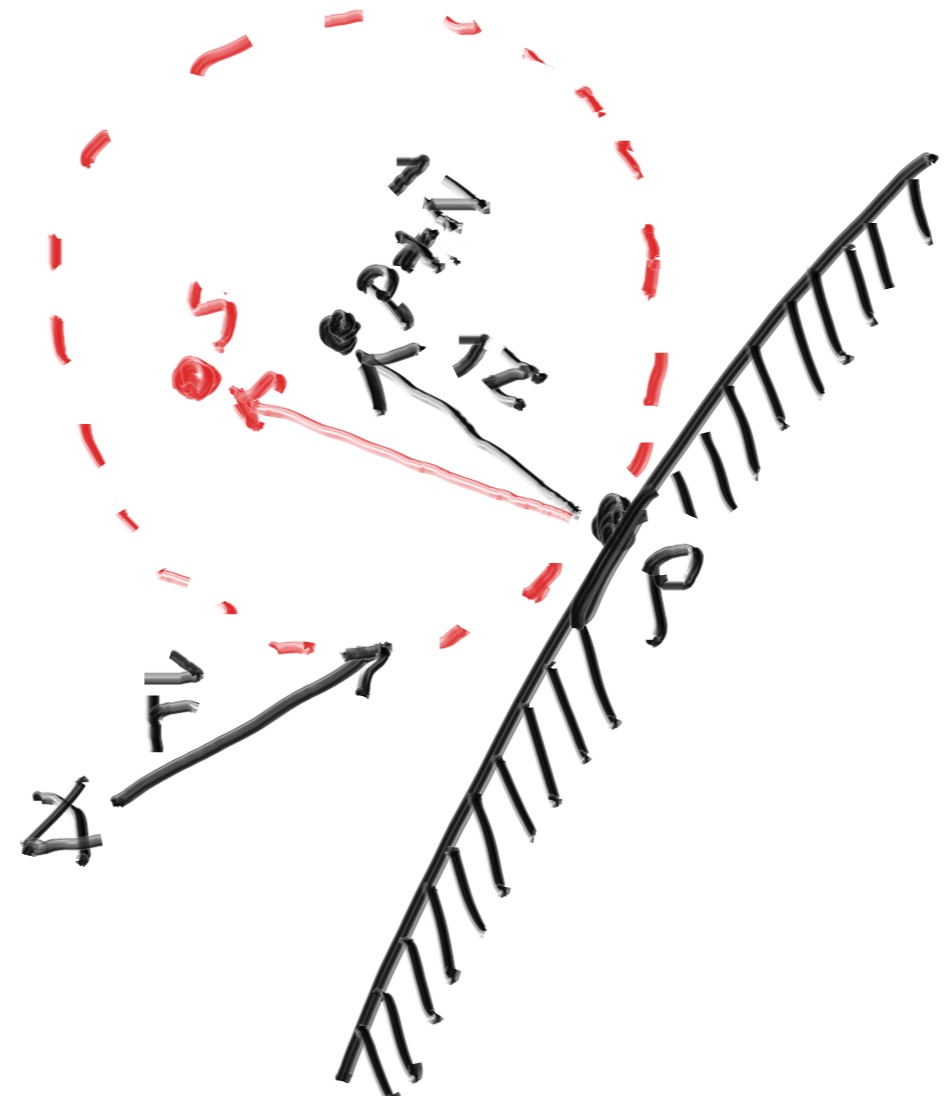
    • 实现方式，在球的表面上均匀采点，小球面均匀采样 \(\mathbf{S}\)，等价于大半球面朗伯采样 \(\mathbf{S}_2\)
    • 小球面：\(\mathrm{d}\omega\)
    • 大球面：\(\mathrm{d}\omega_2\)

\[ \begin{aligned} \mathrm{d}\omega &=\sin{2\phi}\;\mathrm{d}\theta\mathrm{d}2\phi\\ &=2\sin{2\phi}\;\mathrm{d}\theta\mathrm{d}\phi\\ &=4\cos{\phi}\sin{\phi}\;\mathrm{d}\theta\mathrm{d}\phi\\ &=4\cos{\phi}\;\mathrm{d}\omega_2\\ \end{aligned} \]

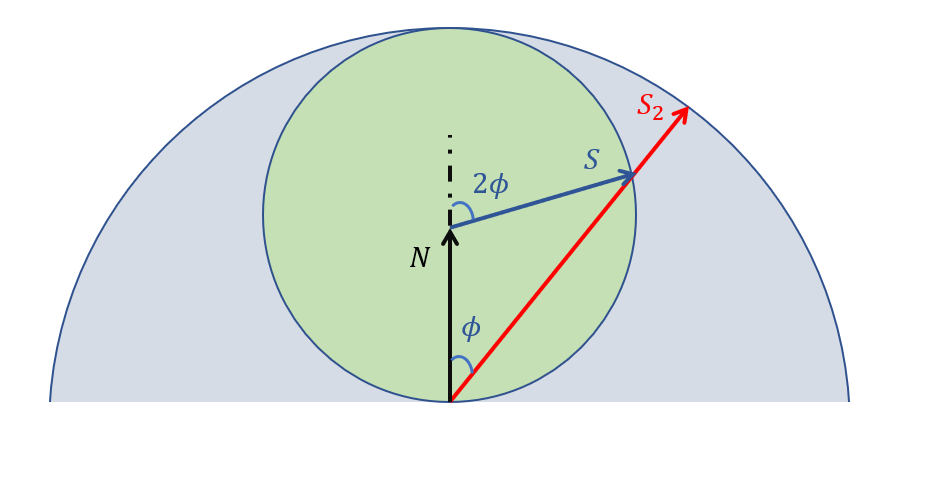
  • 之前还有一种采样方式，随机采一条单位长度的光线，让后判断它和法线是否在同一个法向半球内
    • 法向半球采样

不同采样方式 10spp

  • 法向半球采样

  • 球体表面采样（朗伯采样）

  • 球体内部采样，单位化

  • 球体内部采样

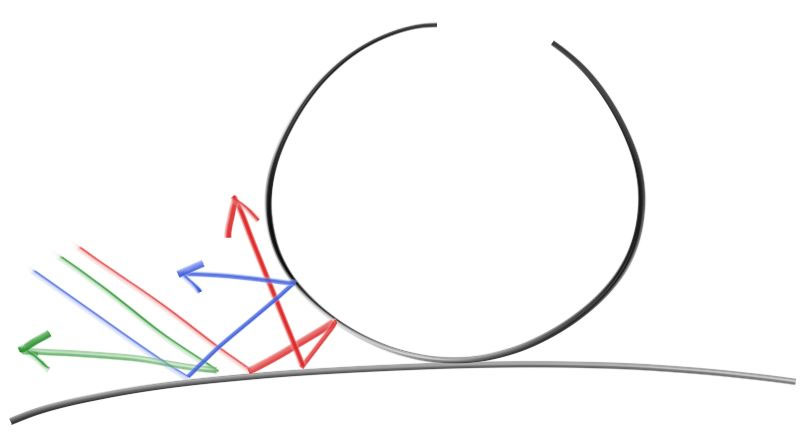
6. 纯镜面材质

磨砂材质

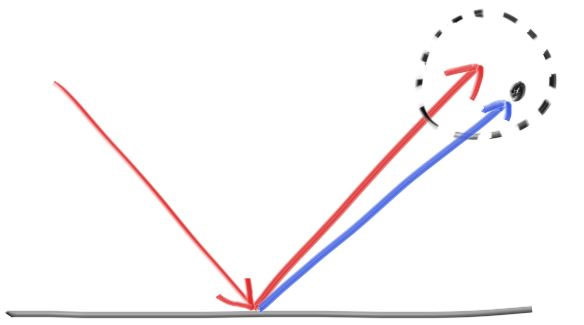
  • 反射方向周围采样一个偏折角

7. 绝缘体材质

  • Dielectrics
    • Clear materials such as water, glass, and diamonds are dielectrics.
  • 同时有折射、反射
  • 实现：每次只取一个方向（折射 / 反射）
  • 折射定律

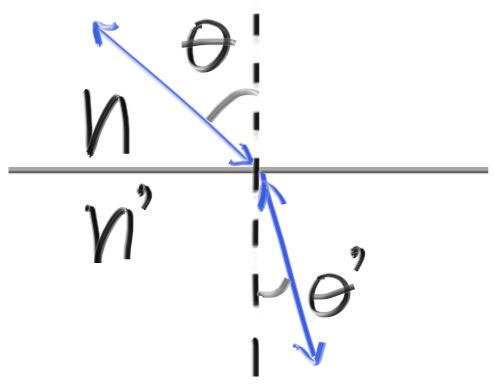\[ \eta \cdot \sin\theta = \eta' \cdot \sin\theta' \]

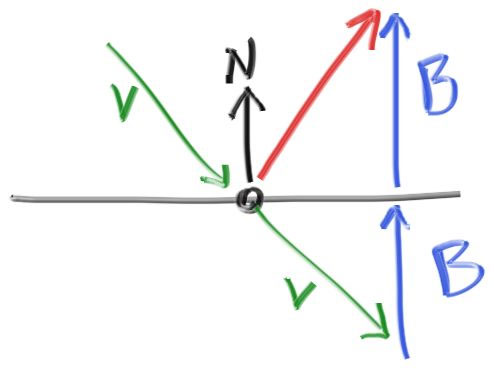
  • 入射方向指向交点，出射方向从交点指出
  • 分量分解，出射光线 \(\mathbf{R'}\)

\[ \mathbf{R'}=\mathbf{R'}_{\bot}+\mathbf{R'}_{\parallel} \]

  • 垂直法线分量

\[ \begin{array}{c} \eta'\mathbf{R'}_{\bot}=\eta\mathbf{R}_{\bot}=\eta(\mathbf{R}-\mathbf{R'}_{\parallel})=\eta(\mathbf{R}+\cos\theta\mathbf{n})=\eta(\mathbf{R}-(\mathbf{n}\cdot\mathbf{R})\mathbf{n})\\ \mathbf{R'}_{\bot}=\dfrac{\eta}{\eta'}(\mathbf{R}-(\mathbf{n}\cdot\mathbf{R})\mathbf{n})\\ \end{array} \]

  • 平行法线分量

\[ \mathbf{R'}_{\parallel} = -\sqrt{1 - |\mathbf{R'}_{\bot}|^2} \mathbf{n} \]

Schlick 不等式估计反射的概率

  • 近似菲涅尔项

\[ R(\theta) = R_0 + (1 - R_0)(1 - \cos \theta)^5 \]

\[ R_0=\left(\frac{n_1-n_2}{n_1+n_2}\right)^2 = \left(\dfrac{\dfrac{n_1}{n_2}-1}{\dfrac{n_1}{n_2}+1}\right)^2= \left(\dfrac{\dfrac{n_2}{n_1}-1}{\dfrac{n_2}{n_1}+1}\right)^2 \]

球的法向反向

  • 半径设置为负数，这样可以让法相反向
    • 因为我们在计算法相的时候，有一个除以半径的操作

8. 相机

  • 相机参数，y-z 平面

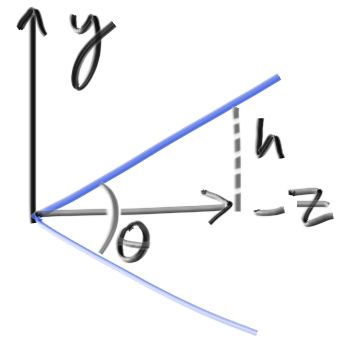
  • lookfrom、lookat

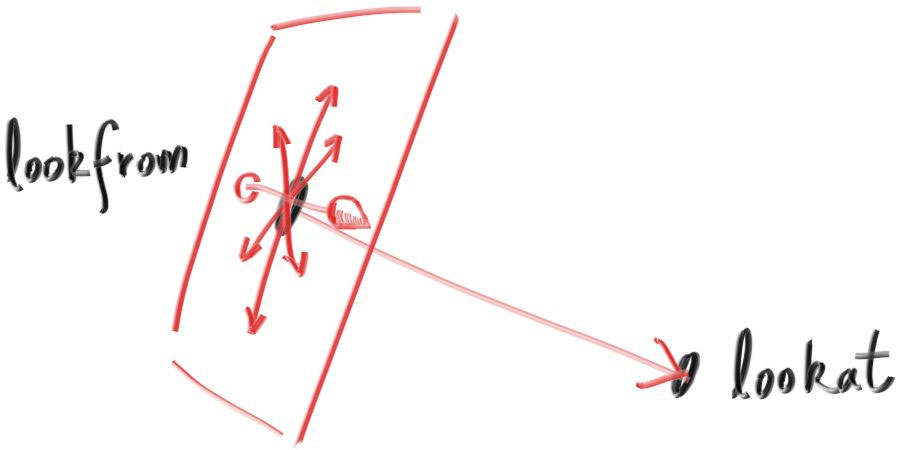
  • vup：用于表示相机的倾斜程度
    • 从而建立起坐标系

1
2
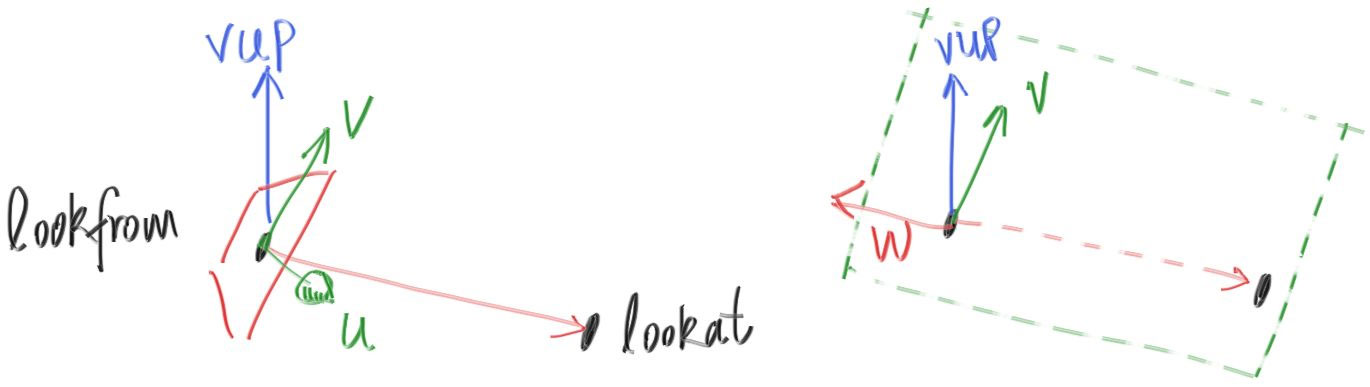
3
vec3 w = (lookfrom - lookat).unit_vector();
vec3 u = vup.cross(w).unit_vector();
vec3 v = w.cross(u);

9. 透镜焦距效果

  • defocus blur
  • depth of field：景深
  • focus distance
    • the distance between the projection point and the plane where everything is in perfect focus
    • controlled by the distance between the lens and the film/sensor
  • focal length：焦距
    • the distance between the projection point and the image plane
  • aperture：光圈
    • 大光圈 \(\to\) 高进光量、浅景深

薄透镜近似

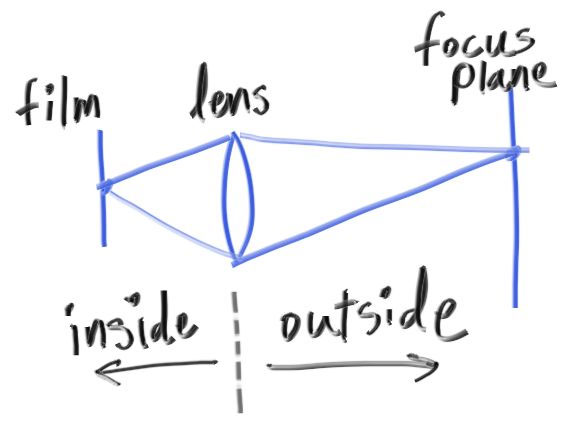
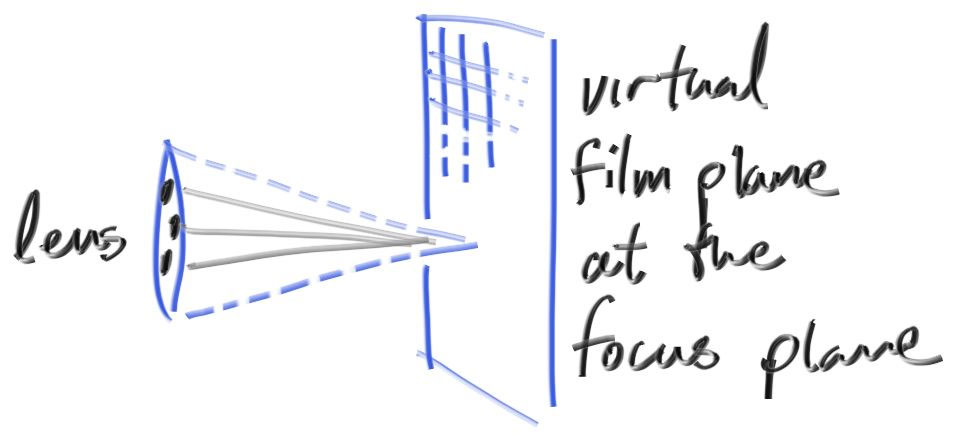
  • 我们不需要模拟内部结构，film 上的结果知识 focus plane 上物体的倒影罢了，因此我们可以直接对 focus plane 上的物体成像（二者是等价的）
  • 也就是说，从透镜上采样即可

10. 结果图展示

spp

场景 1

  • 1000spp

  • 10000spp

场景 2

  • 1spp

  • 10spp

  • 100spp

  • 1000spp

最终结果

  • 景深效果：1000spp
1
2
3
4
5
point3 lookfrom(13, 2, 3);
point3 lookat(0, 0, 0);
vec3 vup(0, 1, 0);
double dist_to_focus = 10.0; // focus plane
double aperture = 0.5;

  • 无景深效果：1000spp

11. 说明

  • OK

    • 物体：球体
    • 相机：任意位置
    • 材质：diffuse、metal(glossy/specular)、dielectric

  • NO

    • 光源
    • 加速结构
    • 三角面片