计算方法B.裴玉茹.06.线性方程组(3)

• PPT（线性方程组）

线性方程组

5. 共轭梯度方法

• 共轭梯度方法
  • 求解 \(n\times n\) 正定线性方程组迭代方法
  • \(n\) 步求解线性方程组（直接方法）
  • \(x=x+tv\)
    • 共轭梯度方向
  • 对矩阵进行预处理，只需大约 \(n\) 步收敛
• 示意图
  • 绿色：梯度下降
  • 红色：共轭梯度下降

(1) 预备知识

定理 1

• 向量 \(x^{\ast}\) 是正定线性方程组 \(Ax=b\) 的解当且仅当 \(x^{\ast}\) 最小化函数 $g(x)=x,Ax,-2x,b$
• 证明思路：\(g(x+tv)\) ，偏导为 0 时的 \(x\) 条件

算法

• 迭代算法如下
• 找到某个方向 \(v^{(k)}\) ，然后最小化这个函数（求出 \(t_k\) ）

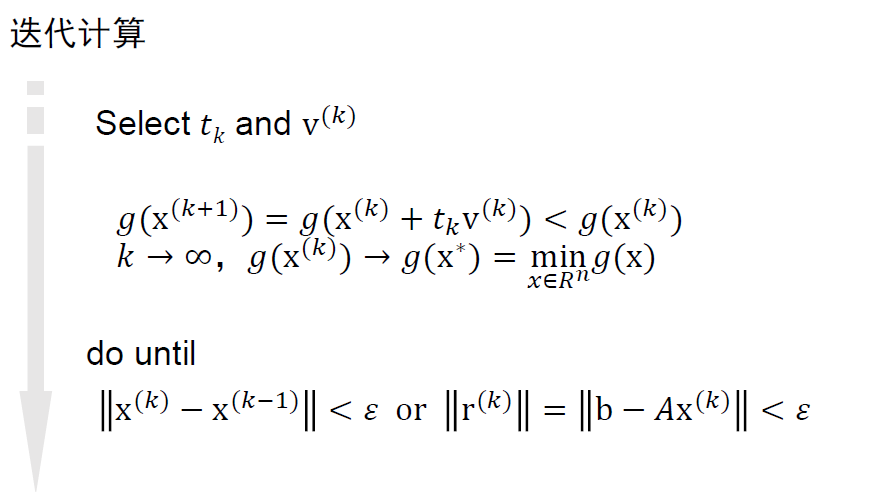
• 如何确定 \(v^{(k)}\)

(2) 最速下降

• 每次的方向规定为负梯度方向
  • 最速下降方法对非线性方程组和优化问题有很好的应用
  • 但由于收敛速度慢，不适用于线性方程组
• 算法步骤

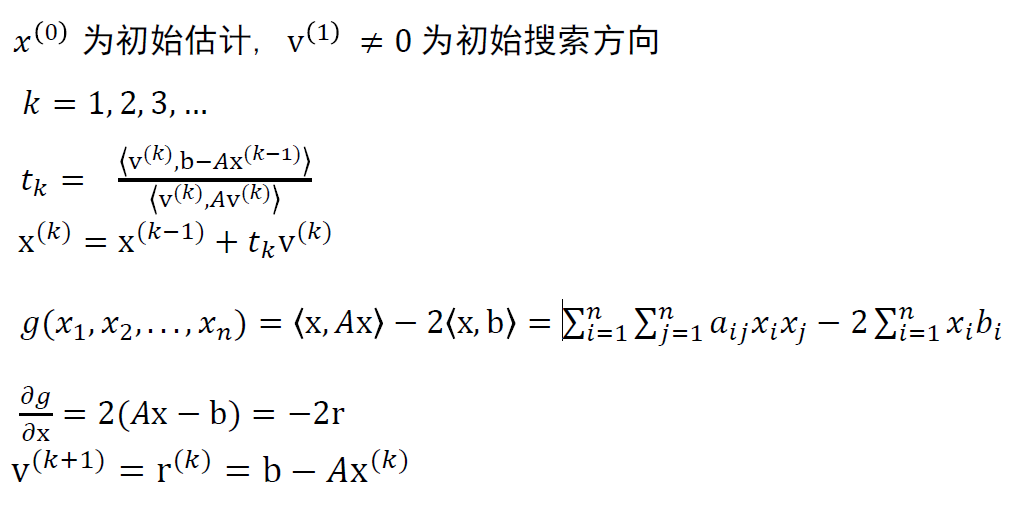
(3) 共轭梯度下降

• note
• 正定矩阵 \(A\)
  • \(A-\)正交条件

\[ \langle v^{(i)},Av^{(j)}\rangle=0,i\ne j \]

定理 1

• 共轭梯度方法定理

证明

• 直接展开证明即可

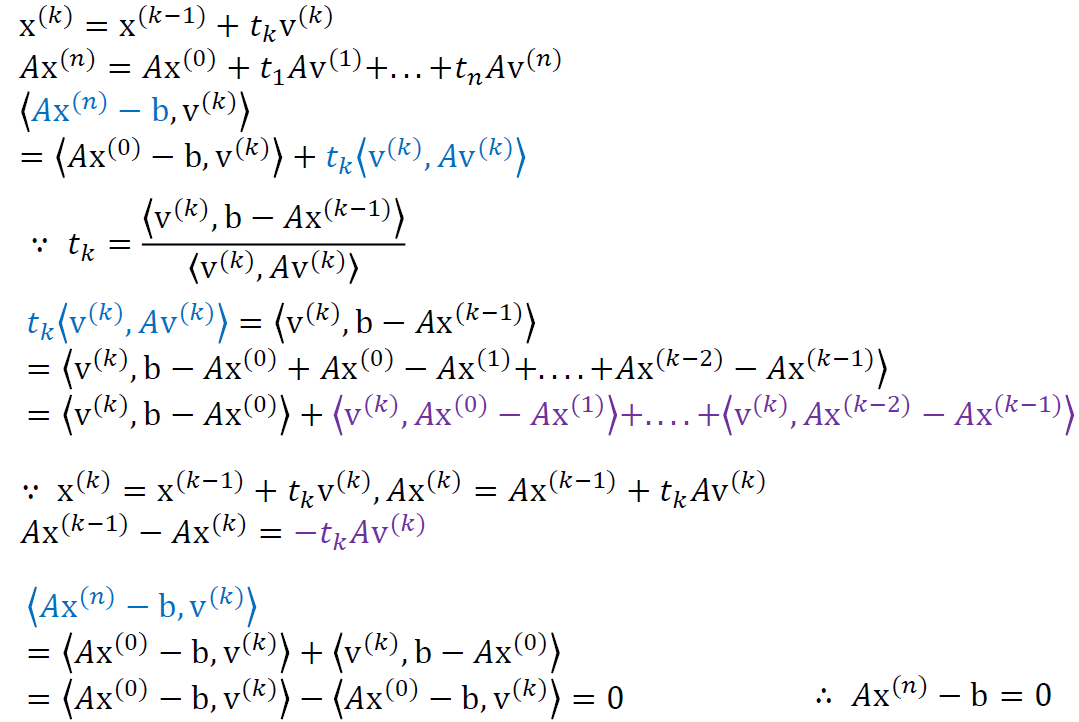
• 第 3 行到第 4 行：代入第 2 行的结果，利用 \(A-\)正交性
• 第 12 行：紫色部分全为 0

定理 2

• 共轭方向法的剩余向量 \(r^{(k)}\) 满足 \(\langle r^{(k)},v^{(j)}\rangle=0\)，\(j=1,\cdots,k\)

\[ \begin{array}{c} r^{(k)}=b-Ax^{(k)}\\ r^{(k+1)}=r^{(k)}-t_{k+1}Av^{(k+1)}\\ \end{array} \]

证明

• 初始方向是余项方向：\(v^{(1)}=r^{(0)}\)

定理 3

• 共轭方法中的余项 \(r^{(k)}\) 满足 \(\langle r^{(k)},r^{(j)}\rangle=0\)，\(j=1,\cdots,k-1\)

证明

• 如何确定搜索方向 \(v^{(k)}\)，由如下式子决定（\(s_{k-1}\) 用于调整至 \(A-\)正交条件）

\[ v^{(k)}=r^{(k-1)}+s_{k-1}v^{(k-1)} \]

• 证明

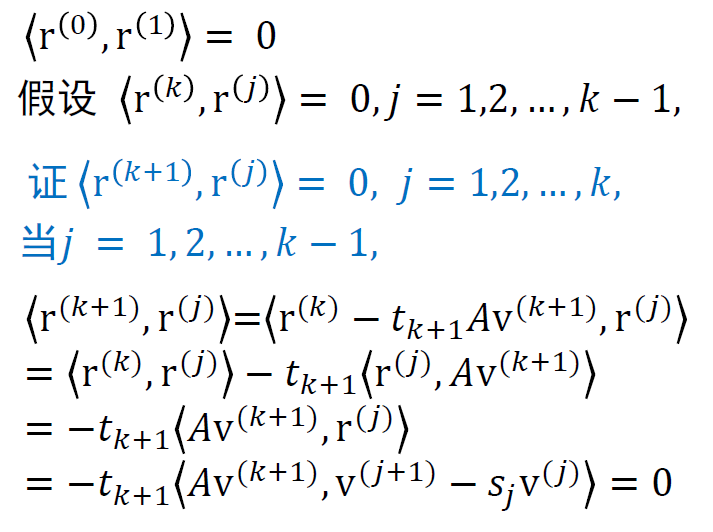
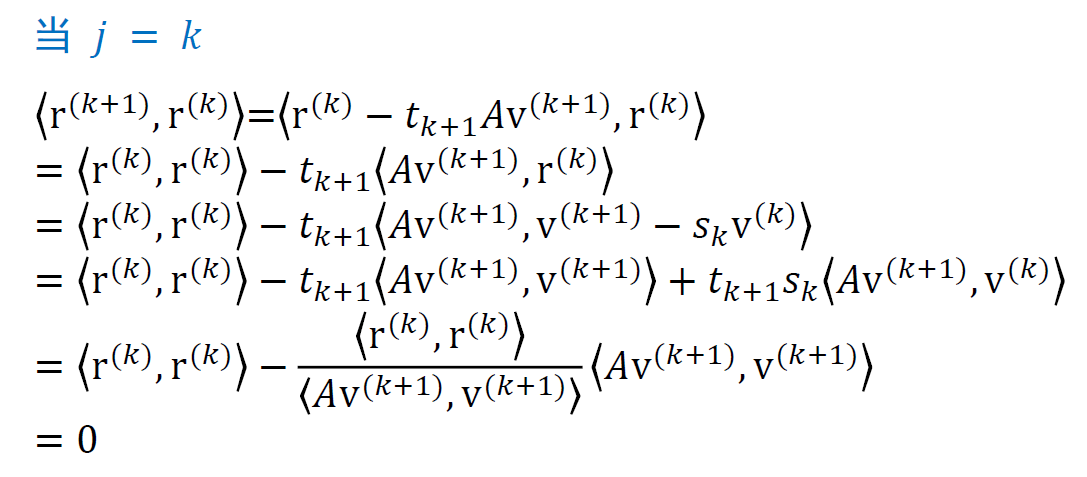
共轭梯度算法如下

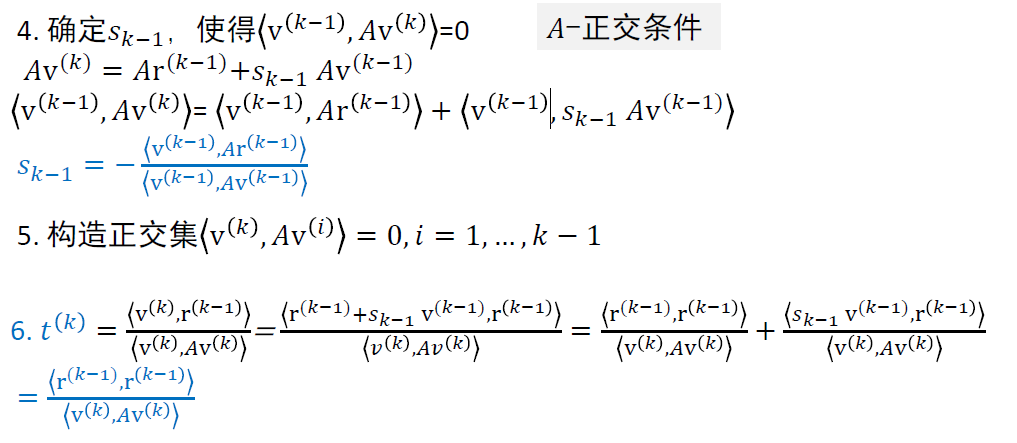
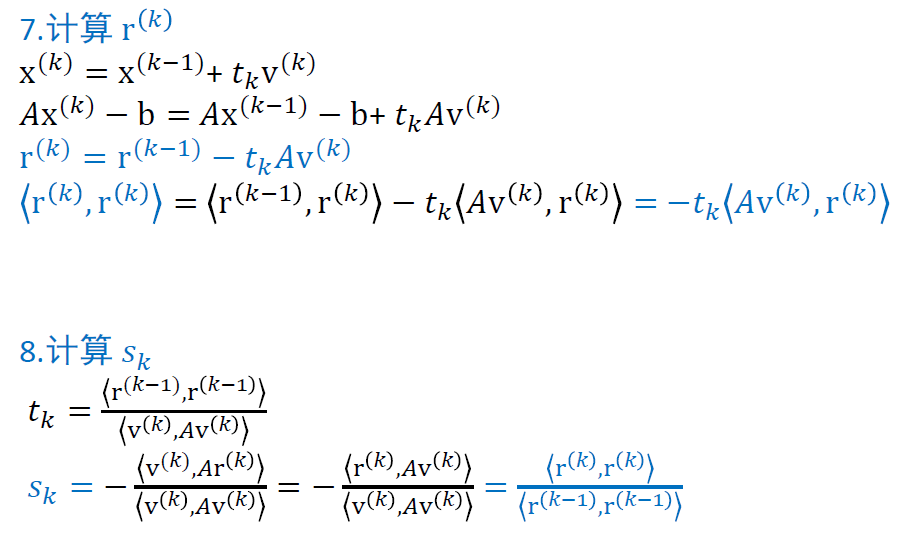
正交集证明

• 为什么 \(v^{(k)}\) 和 \(v^{(k-1)}\) 正交就可以推导得到正交集
• \(j<k-1\)

\[ \begin{aligned} \langle Av^{(k)},v^{(j)}\rangle&=\langle Ar^{(k-1)},v^{(j)}\rangle+s_{k-1}\langle Av^{(k-1)},v^{(j)}\rangle\\ &=\langle Ar^{(k-1)},v^{(j)}\rangle\\ \end{aligned} \]

• 而根据如下式子，根据 \(A\) 正定，证毕

\[ \langle r^{(k-1)},Av^{(j)}\rangle=\langle r^{(k-1)},\dfrac{r^{(j-1)}-r^{(j)}}{t^{(j)}}\rangle=0 \]

• \(r^{(k-1)}\) 和 \(r^{(j-1)},r^{(j)}\) 正交，用到归纳 \(\{v^{(1)},\cdots,v^{(k-1)}\}\) 为正交集

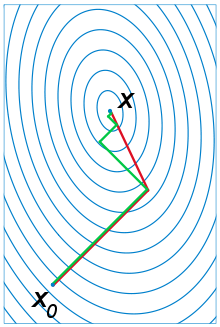
(4) 预条件共轭梯度法

• note
• 降低 \(A\) 条件数
• 选择一个非奇异条件矩阵 \(C\)，使 \(\tilde{A}=C^{-1}A(C^{-1})^{T}\) 条件更好

\[ \begin{array}{c} \tilde{A}=C^{-1}A(C^{-1})^{T}\\ \tilde{A}\tilde{x}=\tilde{b}\\ 记号:\tilde{x}=C^{T}x,\tilde{b}=C^{-1}\tilde{b}\\ A\tilde{x}=C^{-1}Ax=C^{-1}b\\ \end{array} \]

• \(C^{-1}Ax=C^{-1}b\)
• 具体算法：根据上面的算法求解 \(\tilde{A}\tilde{x}=\tilde{b}\)，过程中转化到解 \(x\)